Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-30T20:59:58.590Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ERDŐS–SZEKERES PROBLEM AND AN INDUCED RAMSEY QUESTION

Part of: Extremal combinatorics

Published online by Cambridge University Press:  12 April 2019

Dhruv Mubayi  and
Andrew Suk
Dhruv Mubayi
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois, Chicago, IL 60607, U.S.A. email [email protected]
Andrew Suk
Affiliation:
Department of Mathematics, University of California at San Diego, La Jolla, CA 92093, U.S.A. email [email protected]
Get access

Abstract

Motivated by the Erdős–Szekeres convex polytope conjecture in 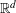$\mathbb{R}^{d}$, we initiate the study of the following induced Ramsey problem for hypergraphs. Given integers 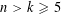$n>k\geqslant 5$, what is the minimum integer 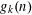$g_{k}(n)$ such that any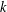$k$-uniform hypergraph on 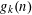$g_{k}(n)$ vertices with the property that any set of 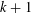$k+1$ vertices induces 0, 2, or 4 edges, contains an independent set of size $n$. Our main result shows that 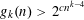$g_{k}(n)>2^{cn^{k-4}}$, where 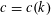$c=c(k)$.

MSC classification

Primary: 05D10: Ramsey theory
Type
Research Article
Information
Mathematika , Volume 65 , Issue 3 , 2019 , pp. 702 - 707
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author’s research was partially supported by NSF grant DMS-1763317. The second author was supported by an NSF CAREER award and an Alfred Sloan Fellowship.

References

Erdős, P. and Szekeres, G., A combinatorial problem in geometry. Compos. Math. 2 1935, 463–470.Google Scholar
Erdős, P. and Szekeres, G., On some extremum problems in elementary geometry. Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 3–4 1960–61, 53–62.Google Scholar
Károlyi, G., Ramsey-remainder for convex sets and the Erdős–Szekeres theorem. Discrete Appl. Math. 109 2001, 163–175.Google Scholar
Károlyi, G. and Valtr, P., Point configurations in d-space without large subsets in convex position. Discrete Comput. Geom. 30 2003, 277–286.Google Scholar
Matoušek, J., Lectures in Discrete Geometry, Springer (2002).Google Scholar
Motzkin, T., Cooperative classes of finite sets in one and more dimensions. J. Combin. Theory 3 1967, 244–251.Google Scholar
Szekeres, G. and Peters, L., Computer solution to the 17-point Erdős–Szekeres problem. ANZIAM J. 48 2006, 151–164.Google Scholar
Suk, A., On the Erdős–Szekeres convex polygon problem. J. Amer. Math. Soc. 30 2017, 1047–1053.Google Scholar