Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T13:34:08.119Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DISTRIBUTION OF 2-SELMER RANKS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH PARTIAL TWO-TORSION

Part of: Multiplicative number theory Arithmetic algebraic geometry Curves

Published online by Cambridge University Press:  04 May 2015

Zev Klagsbrun  and
Robert J. Lemke Oliver
Zev Klagsbrun
Affiliation:
Center for Communications Research, 4320 Westerra Court, San Diego, CA 92121, U.S.A. email [email protected]
Robert J. Lemke Oliver
Affiliation:
Department of Mathematics, Stanford University, Building 380, Stanford, CA 94305, U.S.A. email [email protected]
Get access

Abstract

This paper presents a new result concerning the distribution of 2-Selmer ranks in the quadratic twist family of an elliptic curve over an arbitrary number field 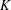$K$ with a single point of order two that does not have a cyclic 4-isogeny defined over its two-division field. We prove that at least half of all the quadratic twists of such an elliptic curve have arbitrarily large 2-Selmer rank, showing that the distribution of 2-Selmer ranks in the quadratic twist family of such an elliptic curve differs from the distribution of 2-Selmer ranks in the quadratic twist family of an elliptic curve having either no rational two-torsion or full rational two-torsion.

MSC classification

Primary: 11G05: Elliptic curves over global fields 11N45: Asymptotic results on counting functions for algebraic and topological structures 14H52: Elliptic curves
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 67 - 78
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cassels, J. W. S., Arithmetic on curves of genus 1. VIII: On the conjectures of Birch and Swinnerton-Dyer. J. reine angew. Math. 217 1965, 180–199.CrossRefGoogle Scholar
Flynn, E. V. and Grattoni, C., Descent via isogeny on elliptic curves with large rational torsion subgroups. J. Symbolic Comput. 43(4) 2008, 293–303.CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., Sieving and the Erdős–Kac theorem. In Equidistribution in Number Theory, an Introduction (NATO Sci. Ser. II Math. Phys. Chem. 237), Springer (Dordrecht, 2007), 15–27; MR 2290492.Google Scholar
Heath-Brown, D. R., The size of Selmer groups for the congruent number problem, II. Invent. Math. 118(1) 1994, 331–370.CrossRefGoogle Scholar
Kane, D., On the ranks of the 2-Selmer groups of twists of a given elliptic curve. Algebra Number Theory 7(5) 2013, 1253–1279.CrossRefGoogle Scholar
Klagsbrun, Z., Selmer ranks of quadratic twists of elliptic curves with partial rational two-torsion. Preprint, 2011, arXiv:1201.5408.Google Scholar
Klagsbrun, Z., Mazur, B. and Rubin, K., A Markov model for Selmer ranks in families of twists. Compos. Math. 150(7) 2014, 1077–1106.CrossRefGoogle Scholar
Klagsbrun, Z. and Lemke Oliver, R., The distribution of the Tamagawa ratio in the family of elliptic curves with a two-torsion point. Res. Math. Sci. 1 2014, paper 15, doi:10.1186/s40687-014-0015-4.CrossRefGoogle Scholar
Klagsbrun, Z. and Lemke Oliver, R., Elliptic curves and the joint distribution of additive functions (in preparation).Google Scholar
Swinnerton-Dyer, P., The effect of twisting on the 2-Selmer group. In Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 145, Cambridge University Press (2008), 513–526.Google Scholar
Xiong, M., On Selmer groups of quadratic twists of elliptic curves with a two-torsion over ℚ. Mathematika 59(2) 2013, 303–319.CrossRefGoogle Scholar