Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T07:18:50.127Z Has data issue: false hasContentIssue false
  • English
  • Français

DIMENSIONS OF TRIANGLE SETS

Part of: Discrete geometry Classical measure theory

Published online by Cambridge University Press:  18 December 2018

Han Yu
Han Yu*
Affiliation:
School of Mathematics & Statistics, University of St Andrews, St Andrews, KY16 9SS, U.K. email [email protected]
Get access

Abstract

In this paper we discuss some dimension results for triangle sets of compact sets in 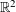$\mathbb{R}^{2}$. In particular we prove that for any compact set 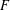$F$ in 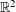$\mathbb{R}^{2}$, the triangle set 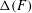$\unicode[STIX]{x1D6E5}(F)$ satisfies

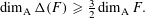$$\begin{eqnarray}\dim _{\text{A}}\unicode[STIX]{x1D6E5}(F)\geqslant {\textstyle \frac{3}{2}}\dim _{\text{A}}F.\end{eqnarray}$$
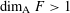If $\dim _{\text{A}}F>1$, then we have
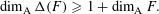$$\begin{eqnarray}\dim _{\text{A}}\unicode[STIX]{x1D6E5}(F)\geqslant 1+\dim _{\text{A}}F.\end{eqnarray}$$
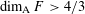 If $\dim _{\text{A}}F>4/3$, then we have the following better bound:
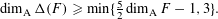$$\begin{eqnarray}\dim _{\text{A}}\unicode[STIX]{x1D6E5}(F)\geqslant \min \{{\textstyle \frac{5}{2}}\dim _{\text{A}}F-1,3\}.\end{eqnarray}$$
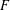 Moreover, if $F$ satisfies a mild separation condition, then the above result holds also for the box dimensions, namely,
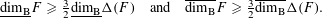$$\begin{eqnarray}\text{}\underline{\dim _{\text{B}}}F\geqslant {\textstyle \frac{3}{2}}\text{}\underline{\dim _{\text{B}}}\unicode[STIX]{x1D6E5}(F)\quad \text{and}\quad \overline{\dim _{\text{B}}}F\geqslant {\textstyle \frac{3}{2}}\overline{\dim _{\text{B}}}\unicode[STIX]{x1D6E5}(F).\end{eqnarray}$$

MSC classification

Primary: 28A80: Fractals
Secondary: 52C10: Erdős problems and related topics of discrete geometry 52C15: Packing and covering in $2$ dimensions 52C35: Arrangements of points, flats, hyperplanes
Type
Research Article
Information
Mathematika , Volume 65 , Issue 2 , 2019 , pp. 311 - 332
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chan, V., Łaba, I. and Pramanik, M., Finite configurations in sparse sets. J. Anal. Math. 128 2016, 289–335.Google Scholar
Falconer, K., Fractal Geometry: Mathematical Foundations and Applications, Wiley (2004).Google Scholar
Fraser, J., Assouad type dimensions and homogeneity of fractals. Trans. Amer. Math. Soc. 366 2014, 6687–6733.Google Scholar
Fraser, J., Distance sets, orthogonal projections, and passing to weak tangents. Israel J. Math. 226 2018, 851–875.Google Scholar
Fraser, J., Howroyd, D. and Yu, H., Dimension growth for iterated sumsets. Math. Z. (to appear). Preprint, 2018, arXiv:1802.03324.Google Scholar
Grafakos, L., Greenleaf, A., Iosevich, A. and Palsson, E., Multilinear generalized Radon transforms and point configurations. Forum Math. 27 2015, 2323–2360.Google Scholar
Greenleaf, A. and Iosevich, A., On triangles determined by subsets of the Euclidean plane, the associated bilinear operators and applications to discrete geometry. Anal. PDE 5(2) 2012, 397–409.Google Scholar
Greenleaf, A., Iosevich, A., Liu, B. and Palsson, E., A group-theoretic viewpoint on Erdős–Falconer problems and the Mattila integral. Rev. Mat. Iberoam. 31(3) 2015, 799–810.Google Scholar
Guth, L. and Katz, N., On the Erdős distances problem in the plane. Ann. of Math. (2) 181 2015, 155–190.Google Scholar
Käenmäki, A., Ojala, T. and Rossi, E., Rigidity of quasisymmetric mappings on self-affine carpets. Int. Math. Res. Not. IMRN 2018 2018, 3769–3799.Google Scholar
Katz, N. and Tao, T., Some connections between Falconer’s Distance set conjecture and sets of Furstenburg type. New York J. Math. 7 2001, 149–187.Google Scholar
Mackay, J. and Tyson, J., Conformal Dimension. Theory and Application (University Lecture Series 54 ), American Mathematical Society (Providence, RI, 2010).Google Scholar
Maga, P., Full dimensional sets without given patterns. Real Anal. Exchange 36(1) 2010/11, 79–90.Google Scholar
Mattila, P., Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics), Cambridge University Press (1999).Google Scholar
Mattila, P., Fourier Analysis and Hausdorff Dimension (Cambridge Studies in Advanced Mathematics), Cambridge University Press (2015).Google Scholar
Shmerkin, P., On the Hausdorff dimension of pinned distance sets. Israel J. Math. (to appear). Preprint, 2017, arXiv:1706.00131.Google Scholar
Shmerkin, P. and Suomala, V., Patterns in random fractals. Amer. J. Math. (to appear). Preprint, 2017, arXiv:1703.09553.Google Scholar