Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
2000.
Monoids, Acts and Categories.
p.
483.
Rasouli, Hamid
Barzegar, Hasan
and
Shahbaz, Leila
2017.
Purity in the category ofS-posets.
Communications in Algebra,
Vol. 45,
Issue. 12,
p.
5053.


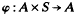 A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right
A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right 