Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T05:06:24.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorially regular polytopes

Published online by Cambridge University Press:  26 February 2010

P. McMullen
P. McMullen
Affiliation:
Department of Pure Mathematics, University of Birmingham, and School of Mathematics and Physics, University of East Anglia, Norwich.
Get access

Extract

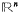Let Pn (n ≥ 0) be an n-polytope, that is, a convex polytope in n-dimensional euclidean space (Grünbaum [5], 3.1), and for 0 ≤ j ≤ n − 1 let 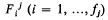be its j-faces. If Pn itself and Ø (the empty set) are also allowed to be faces of Pn, of dimensions n and − 1 respectively, then the set of faces of Pn forms a lattice 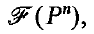partially ordered by inclusion ([5], 3.2). Two polytopes P1n and P2n are said to be combinatorially isomorphic, or of the same combinatorial type if their respective lattices of faces are isomorphic; that is, if there is a one–to–one correspondence between the set of faces of P1n and the set of faces of P2n which preserves the relation of inclusion ([5], 3.2). Similarly, any permutation of the set of faces of Pn which preserves inclusion will be called a (combinatorial) automorphism; it is clear that the set of automorphisms of Pn forms a group Γ(Pn), called the automorphism group of Pn.

Type
Research Article
Information
Mathematika , Volume 14 , Issue 2 , December 1967 , pp. 142 - 150
Copyright
Copyright © University College London 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Coxeter, H. S. M., “The complete enumeration of finite groups of the form Rt 2 = (Ri Rj)k ij = 1 J. Lond. Math. Soc., 10 (1935), 21–25.CrossRefGoogle Scholar
2.Coxeter, H. S. M., “Wythoff's construction for uniform polytopes”, Proc. Lond. Math. Soc., (2), 38 (1935), 327–339.CrossRefGoogle Scholar
3.Coxeter, H. S. M., Regular polytopes (2nd edition, Macmillan, New York, 1963).Google Scholar
4.Du Val, P., Homographies, quaternions and rotations (Oxford, 1964).Google Scholar
5.Grünbaum, B., Convex polytopes (Wiley and Sons, London and New York, 1967).Google Scholar
6.Macbeath, A. M., “Discontinuous groups and birational transformations”, Proc. of Dundee Summer School in Geometry and Topology, Dundee (1961).Google Scholar