Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MacCluer, Barbara
and
Saxe, Karen
2002.
Spectra of composition operators on the bloch and bergman spaces.
Israel Journal of Mathematics,
Vol. 128,
Issue. 1,
p.
325.
Wojtaszczyk, P.
2003.
Vol. 2,
Issue. ,
p.
1671.
Shi, Jihuai
and
Ren, Guangbin
2006.
Coefficient multipliers of mixed norm space in the ball.
Science in China Series A: Mathematics,
Vol. 49,
Issue. 11,
p.
1491.
Jevtić, Miroljub
Vukotić, Dragan
and
Arsenović, Miloš
2016.
Taylor Coefficients and Coefficient Multipliers of Hardy and Bergman-Type Spaces.
Vol. 2,
Issue. ,
p.
247.
Cleanthous, G.
Georgiadis, A. G.
and
Nielsen, M.
2019.
Molecular decomposition and Fourier multipliers for holomorphic Besov and Triebel–Lizorkin spaces.
Monatshefte für Mathematik,
Vol. 188,
Issue. 3,
p.
467.
Zhu, Xiaolin
Fang, Xiang
Guo, Feng
and
Hou, Shengzhao
2023.
Fractional Integration on Mixed Norm Spaces. II.
The Journal of Geometric Analysis,
Vol. 33,
Issue. 5,
Wang, Chun
and
Xu, Tian-Zhou
2024.
Hyers–Ulam Stability of the Coefficient Multipliers on Analytic Hilbert Spaces.
Mediterranean Journal of Mathematics,
Vol. 21,
Issue. 4,
Wang, Chun
2024.
The coefficient multipliers on $ H^2 $ and $ \mathcal{D}^2 $ with Hyers–Ulam stability.
AIMS Mathematics,
Vol. 9,
Issue. 5,
p.
12550.
Li, Zhongkai
and
Wei, Haihua
2024.
Some aspects of the Bergman and Hardy spaces associated with a class of generalized analytic functions.
Journal of Approximation Theory,
Vol. 301,
Issue. ,
p.
106044.


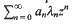 belongs to
belongs to 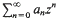 belongs to
belongs to 