Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T18:02:16.644Z Has data issue: false hasContentIssue false
  • English
  • Français

CLOSED SETS WITH THE KAKEYA PROPERTY

Part of: Real and complex geometry

Published online by Cambridge University Press:  23 September 2016

M. Csörnyei ,
K. Héra  and
M. Laczkovich
M. Csörnyei
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, U.S.A. email [email protected]
K. Héra
Affiliation:
Department of Analysis, Institute of Mathematics, Eötvös Loránd University, Pázmány Péter sétány 1/C, 1117 Budapest, Hungary email [email protected]
M. Laczkovich
Affiliation:
Department of Analysis, Institute of Mathematics, Eötvös Loránd University, Pázmány Péter sétány 1/C, 1117 Budapest, Hungary email [email protected]
Get access

Abstract

We say that a planar set 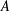$A$ has the Kakeya property if there exist two different positions of 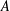$A$ such that 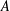$A$ can be continuously moved from the first position to the second within a set of arbitrarily small area. We prove that if 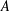$A$ is closed and has the Kakeya property, then the union of the non-trivial connected components of 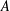$A$ can be covered by a null set which is either the union of parallel lines or the union of concentric circles. In particular, if 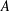$A$ is closed, connected and has the Kakeya property, then 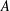$A$ can be covered by a line or a circle.

MSC classification

Primary: 51M25: Length, area and volume
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 184 - 195
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Besicovitch, A. S., On Kakeya’s problem and a similar one. Math. Z. 27 1928, 312–320.Google Scholar
Chang, A. and Csörnyei, M., The Kakeya problem for curves (in preparation).Google Scholar
Cunningham, F. Jr., The Kakeya problem for simply connected and for star-shaped sets. Amer. Math. Monthly 78 1971, 114–129.Google Scholar
Cunningham, F. Jr., Three Kakeya problems. Amer. Math. Monthly 81 1974, 582–592.Google Scholar
Davies, R. O., Some remarks on the Kakeya problem. Proc. Cambridge Philos. Soc. 69 1971, 417–421.Google Scholar
Héra, K. and Laczkovich, M., The Kakeya problem for circular arcs (submitted).Google Scholar
Kuratowski, K., Topology, Vol. II, Academic Press and PWN-Polish Scientific Publishers (1968).Google Scholar
Talagrand, M., Sur la mesure de la projection d’un compact et certaines familles de cercles. Bull. Sci. Math. (2) 104 1980, 225–231.Google Scholar