No CrossRef data available.
Article contents
CLASS NUMBER ONE FROM ANALYTIC RANK TWO
Published online by Cambridge University Press: 03 January 2019
Abstract
We aim to re-prove a theorem conjectured by Gauss, namely there are exactly nine imaginary quadratic fields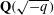 
$\mathbf{Q}(\sqrt{-q})$ with class number one: specifically the list is 
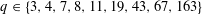$q\in \{3,4,7,8,11,19,43,67,163\}$. Our method initially follows an idea of Goldfeld, but rather than using an elliptic curve of analytic rank three (provided by the Gross–Zagier theorem), we instead use an elliptic curve of analytic rank two, where this 
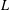$L$-function vanishing can be proven by modular symbols rather than a difficult height formula. It is already clear that Goldfeld’s work yields a constant lower bound for the class number by such means, but unfortunately it seems that even for the best choice of elliptic curve this numerical constant is less than 1, unless one can show non-trivial cancellation in the 
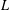$L$-function coefficients restricted to values taken by quadratic forms. To show the latter, we consider a specific analytic rank-two elliptic curve with complex multiplication by 
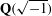$\mathbf{Q}(\sqrt{-1})$, and then by adapting a result of Hooley’s regarding equi-distrbution of roots of a quadratic polynomial to varying moduli, are able to show that there is indeed sufficient coefficient cancellation, giving an effective resolution of class number one. As we use various aspects of the principal form, our proof seems inapplicable for larger class numbers. We also comment on the possibility of using spectral techniques (following Templier and Tsimerman) to show the desired coefficient cancellation, though postpone the details of this to elsewhere.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
References
Atkin, A. O. L. and Lehner, J., Hecke operators on 𝛤0(m). Math. Ann.
185(2) 1970, 134–160,http://eudml.org/doc/161948.Google Scholar
Baker, A., Linear forms in the logarithms of algebraic numbers. Mathematika
13(2) 1966, 204–216, doi:10.1112/S0025579300003971.Google Scholar
Baker, A., A remark on the class number of quadratic fields. Bull. Lond. Math. Soc.
1
1969, 98–102, doi:10.1112/blms/1.1.98.Google Scholar
Baker, A., Imaginary quadratic fields with class number 2. Ann. of Math. (2)
94(1) 1971, 139–152, doi:10.2307/1970739.Google Scholar
Baran, B., A modular curve of level 9 and the class number one problem. J. Number Theory
129(3) 2009, 715–728, doi:10.1016/j.jnt.2008.09.013.Google Scholar
Baran, B., Normalizers of non-split Cartan subgroups, modular curves, and the class number one problem. J. Number Theory
130(12) 2010, 2753–2772, doi:10.1016/j.jnt.2010.06.005.Google Scholar
Blomer, V., Sums of Hecke eigenvalues over values of quadratic polynomials. Int. Math. Res. Not. IMRN
2008(16), rnn059, doi:10.1093/imrn/rnn059.Google Scholar
Braaksma, B. L. J., Asymptotic expansions and analytic continuations for a class of Barnes-integrals. Compos. Math.
15
1962-4, 239–341, http://eudml.org/doc/88877.Google Scholar
Bundschuh, P. and Hock, A., Bestimmung aller imaginär-quadratischen Zahlkörper der Klassenzahl Eins mit Hilfe eines Satzes von Baker (German) [Determination of all imaginary quadratic fields of class number one with the help of a theorem of Baker]. Math. Z.
111(3) 1969, 191–204, doi:10.1007/BF01113285.Google Scholar
Burgess, D. A., On character sums and L-series. II. Proc. Lond. Math. Soc. (3)
13
1963, 524–536, doi:10.1112/plms/s3-13.1.524.Google Scholar
Bykovskii, V. A., A trace formula for the scalar product of Hecke series and its applications. J. Math. Sci.
89(1) 1998, 915–932, doi:10.1007/BF02358528.Google Scholar
Chen, I., On Siegel’s modular curve of level 5 and the class number one problem. J. Number Theory
74(2) 1999, 278–297, doi:10.1006/jnth.1998.2320.Google Scholar
Cremona, J. E., Algorithms for Modular Elliptic Curves, Cambridge University Press (Cambridge, 1992), http://homepages.warwick.ac.uk/
masgaj/book/amec.html.Google Scholar
masgaj/book/amec.html.Google ScholarDavenport, H., Multiplicative Number Theory, 3rd edn.
(Graduate Texts in Mathematics 74
), Springer (New York, 2000), doi:10.1007/978-1-4757-5927-3.Google Scholar
Deuring, M., Imaginäre quadratische Zahlkörper mit der Klassenzahl 1 (German) [Imaginary quadratic fields with class number 1]. Math. Z.
37
1933, 405–415, http://eudml.org/doc/168455.Google Scholar
Deuring, M., Zetafunktionen quadratischer Formen (German) [Zeta-functions of quadratic forms]. J. Reine Angew. Math.
172
1935, 226–252, http://eudml.org/doc/149913.Google Scholar
Deuring, M., Die Zetafunktion einer algebraischen Kurve vom Geschlechte Eins (German) [The zeta-function of an algebraic curve of genus one]. Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. Math.-Phys.-Chem. Ab
1953
1953, 85–94.Google Scholar
Deuring, M., Imaginäre quadratische Zahlkörper mit der Klassenzal Eins (German) [Imaginary quadratic fields with class number one]. Invent. Math.
5
1968, 169–179, doi:10.1007/BF01425548.Google Scholar
Lejeune Dirichlet, G., Recherches sur diverses applications de l’Analyse infinitésimale à la Théorie des Nombres (French) [Some diverse applications of the infinitesimal analysis in number theory]. J. Reine Angew. Math.
19(1839), 324–369, ibid.
21 (1840), 134–155.http://resolver.sub.uni-goettingen.de/purl?GDZPPN002142007,http://resolver.sub.uni-goettingen.de/purl?GDZPPN002142473.Google Scholar
Lejuene Dirichlet, P. G., with supplement by R. Dedekind, Vorlesungen über Zahlentheorie (German) [Lectures on number theory]. Vieweg und Sohn, 1871. http://archive.org/details/vorlesungenberz04dedegoog.Google Scholar
Duke, W., Hyperbolic distribution problems and half-integral weight Maass forms. Invent. Math.
92(1) 1988, 73–90, doi:10.1007/BF01393993.Google Scholar
Duke, W., Friedlander, J. B. and Iwaniec, H., Equidistribution of roots of a quadratic congruence to prime moduli. Ann. of Math. (2)
141(2) 1995, 423–441, doi:10.2307/2118527.Google Scholar
Eulero [L. Euler], L., De numeris, qui sunt aggregata duorum quadratorum (Latin) [On numbers which are the sum of two squares]. Novi Commentarii academiæ scientiarum Petropolitanæ
4(1758), 3–40, http://eulerarchive.maa.org/pages/E228.html.Google Scholar
Gauss, C. F., Disquisitiones Arithmeticae (Latin) [Arithmetical investigations] (1801). From his complete works (1863): http://eudml.org/doc/202621; English translation: A. A. Clarke, Disquisitiones Arithmeticae, Yale University Press (1965).Google Scholar
Gelfond, A. O., Transcendental and Algebraic Numbers. Translated from the first Russian edition (1952) by L. F. Boron, Dover (1960, 2015).Google Scholar
Goldfeld, D., The class number of quadratic fields and the conjectures of Birch and Swinnerton-Dyer. Ann. Sc. Norm. Super. Pisa Cl. Sci. (4)
3(4) 1976, 624–663, http://eudml.org/doc/83732.Google Scholar
Gronwall, T. H., Sur les séries de Dirichlet correspondant à des caractéres complexes (French) [On Dirichlet series of complex characters]. Rend. Circ. Mat. Palermo (2)
35
1913, 145–159, doi:10.1007/BF03015596.Google Scholar
Gross, B. H. and Zagier, D. B., Heegner points and derivatives of L-series. Invent. Math.
84(2) 1986, 225–320, http://eudml.org/doc/143341.Google Scholar
Hardy, G. H. and Ramanujan, S., The normal number of prime factors of a number n
. Q. J. Math.
48
1917, 76–92.Google Scholar
Heath-Brown, D. R., Mathematical Reviews #2764153, 2011m:11071.http://mathscinet.ams.org/mathscinet-getitem?mr=2764153.Google Scholar
Hecke, E., Eine neue Art von Zetafunktionen und ihre Beziehungen zur Verteilung der Primzahlen. I, II (German) [A new kind of zeta-function and its relation to the distribution of prime numbers]. Math. Z.
1(4) 1918, 357–376, ibid.
6 (1920), 11–51. http://eudml.org/doc/167468,http://eudml.org/doc/167556.Google Scholar
Hecke, E., Über Modulfunktionen und die Dirichletschen Reihen mit Eulerscher Produktentwicklung. I-II (German) [On modular functions and Dirichlet series with Euler products]. Math. Ann.
114
1937, 1–28, 316–351. http://eudml.org/doc/159899, http://eudml.org/doc/159919.Google Scholar
Heegner, K., Diophantische Analysis und Modulfunktionen (German) [Diophantine analysis and modular functions]. Math. Z.
56
1952, 227–253, http://eudml.org/doc/169287.Google Scholar
Heilbronn, H., On the class number in imaginary quadratic fields. Q. J. Math. Oxford
5(1) 1934, 150–160, doi:10.1093/qmath/os-5.1.150.Google Scholar
Heilbronn, H. and Linfoot, E. H., On the imaginary quadratic corpora of class-number one. Q. J. Math. Oxford
5(1) 1934, 293–301, doi:10.1093/qmath/os-5.1.293.Google Scholar
Hejhal, D. A., Roots of quadratic congruences and eigenvalues of the non-Euclidean Laplacian. In The Selberg Trace Formula and Related Topics
(Contemporary Mathematics 53
) (eds Hejhal, D. A., Sarnak, P. and Terras, A. A.), American Mathematical Society (Providence, RI, 1986), doi:10.1090/conm/053/853563.Google Scholar
Hooley, C., On the number of divisors of a quadratic polynomial. Acta Math.
110
1963, 97–114, doi:10.1007/BF02391856.Google Scholar
Hooley, C., On the distribution of the roots of polynomial congruences. Mathematika
11
1964, 39–49, doi:10.1112/S0025579300003466.Google Scholar
Iwaniec, H., Fourier coefficients of modular forms of half-integral weight. Invent. Math.
87
1987, 385–402, http://eudml.org/doc/143426.Google Scholar
Iwaniec, H., Topics in Classical Automorphic Forms
(Graduate Studies in Mathematics 17
), American Mathematical Society (Providence, RI, 1997), doi:10.1090/gsm/017.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory
(American Mathematical Society Colloquium Publications 53
), American Mathematical Society (Providence, RI, 2004), doi:10.1090/coll/053.Google Scholar
Jacobi, C. G. J., Observatio arithmetica de numero classium divisorum quadraticorum formae yy + Azz, designante A numerum primum formae 4n + 3 (Latin) [An arithmetic observation on the class number of quadratic forms y
2 + Az
2 where A is a prime congruent to 3 mod 4]. J. Reine Angew. Math.
9
1832, 189–192,http://www.digizeitschriften.de/dms/resolveppn/?PID=GDZPPN002138727.Google Scholar
Kenku, M. A., A note on the integral points of a modular curve of level 7. Mathematika
32(1) 1985, 45–48, doi:10.1112/S0025579300010846.Google Scholar
de La Vallée Poussin, Ch.-J., Sur la fonction 𝜁(s) de Riemann et le nombre des nombres premieres inférieurs a une limite donnée (French) [On the Riemann 𝜁-function and the number of prime numbers less than a given limit]. Mem. Courronnes et Autres Mem. Pub. Acad. Roy. Sci. Lettres Beaux-Arts Belgique
59
1899/1900, http://archive.org/details/surlafonctionze00pousgoog.Google Scholar
Landau, E., Über imaginär-quadratischer Zahlkörper mit gleicher Klassenzahl (German) [On imaginary quadratic fields with the same class number]. Nachr. Ges. Wiss. Göttingen, Math.-Phys. Kl.
1918, 277–284, http://www.digizeitschriften.de/dms/resolveppn/?PID=GDZPPN002505134.Google Scholar
Landau, E., Über die Klassenzahl imaginär-quadratischer Zahlkörper (German) [On the class number of imaginary quadratic fields]. Nachr. Ges. Wiss. Göttingen, Math.-Phys. Kl.
1918, 285–295, http://www.digizeitschriften.de/dms/resolveppn/?PID=GDZPPN002505142.Google Scholar
Landau, E., Bemerkungen zum Heilbronnschen Satz (German) [Remarks about Heilbronn’s theorem]. Acta Arith.
1
1935, 1–18, http://eudml.org/doc/205049.Google Scholar
Linnik, U. V., On the least prime in an arithmetic progression II. The Deuring–Heilbronn phenomenon. Rec. Math. [Mat. Sbornik.]
15(3) 1944, 347–368,http://mi.mathnet.ru/eng/msb6202.Google Scholar
Littlewood, J. E., On the class number of the corpus P (√-k). Proc. Lond. Math. Soc. (3)
27
1928, 358–372, http://plms.oxfordjournals.org/content/s2-27/1/358.full.pdf+html.Google Scholar
Manin, Ju. I., Parabolic points and zeta-functions of modular curves. Math. USSR Izvestia (Translated)
6
1972, 19–64, doi:10.1070/IM1972v006n01ABEH001867.Google Scholar
McCurley, K. S., Explicit zero-free regions for Dirichlet L-functions. J. Number Theory
19(1) 1984, 7–32, doi:10.1016/0022-314X(84)90089-1.Google Scholar
Oesterlé, J., Nombres de classes des corps quadratiques imaginaires (French) [Class numbers of imaginary quadratic fields]. Sém. Bourbaki
26
1983–1984, 309–323,http://eudml.org/doc/110032.Google Scholar
Perron, O., Zur Theorie der Dirichletschen Reihen (German) [On the theory of Dirichlet series]. J. Reine Angew. Math.
134
1908, 95–143, http://eudml.org/doc/149285.Google Scholar
Schoof, R. and Tzanakis, N., Integral points of a modular curve of level 11. Acta Arith.
152(1) 2012, 39–49, doi:10.4064/aa152-1-4.Google Scholar
Serre, J.-P., 𝛥 = ab
2 - 4ac
. Math. Medley (Singapore Math. Soc.)
13
1985, 1–10,http://sms.math.nus.edu.sg/smsmedley/smsmedley.aspx#Vol-13.Google Scholar
Serre, J.-P., Lectures on the Mordell–Weil Theorem
(Aspects of Mathematics 15
), Friedr. Vieweg & Sohn (Braunschweig, 1989, 1997). Translated and edited by M. Brown from notes by M. Waldschmidt, doi:10.1007/978-3-663-10632-6.Google Scholar
Shimura, G., On the holomorphy of certain Dirichlet series. Proc. Lond. Math. Soc. (3)
31(1) 1975, 79–98, doi:10.1112/plms/s3-31.1.79.Google Scholar
Siegel, C. L., Über die Classenzahl quadratischer Zahlkörper (German) [On the class number of quadratic fields]. Acta Arith.
1
1935, 83–86, https://eudml.org/doc/205054.Google Scholar
Siegel, C. L., Zum Beweise des Starkschen Satzes (German) [Some remarks on Stark’s theorem]. Invent. Math.
5(3) 1968, 180–191, http://eudml.org/doc/141914.Google Scholar
Sorenson, J. P., Sieving for pseudosquares and pseudocubes in parallel using doubly-focused enumeration and wheel datastructures. In Algorithmic Number Theory (ANTS 2010)
(Lecture Notes in Computer Science 6197
) (eds Hanrot, G., Morain, F. and Thomé, E.), Springer
331–339, doi:10.1007/978-3-642-14518-6-26.Google Scholar
Stark, H., On complex quadratic fields with class number equal to one. Trans. Amer. Math. Soc.
122
1966, 112–119, doi:10.1090/S0002-9947-1966-0195845-4.Google Scholar
Stark, H. M., A complete determination of the complex quadratic fields of class-number one. Michigan Math. J.
14(1) 1967, 1–27, doi:10.1307/mmj/1028999653.Google Scholar
Stark, H. M., On the “gap” in a theorem of Heegner. J. Number Theory
1
1969, 16–27, doi:10.1016/0022-314X(69)90023-7.Google Scholar
Stark, H. M., A historical note on complex quadratic fields with class-number one. Proc. Amer. Math. Soc.
21
1969, 254–255, doi:10.1090/S0002-9939-1969-0237461-X.Google Scholar
Stark, H. M., The role of modular functions in a class-number problem. J. Number Theory
1(2) 1969, 252–260, doi:10.1016/0022-314X(69)90044-4.Google Scholar
Stark, H. M., Recent Advances in Determining all Complex Quadratic Fields of a Given Class-Number
(Proceedings of Symposia in Pure Mathematics XX
) (ed. Lewis, D. J.), American Mathematical Society (Providence, RI, 1971), 401–414, http://www.ams.org/books/pspum/020/0316421.Google Scholar
Stark, H. M., A transcendence theorem for class-number problems. Ann. of Math. (2)
94(1) 1971, 153–173, doi:10.2307/1970740.Google Scholar
Stark, H. M., The Gauss class-number problems. In Analytic Number Theory
(Clay Mathematics Proceedings 7
) (eds Duke, W. and Tschinkel, Y.), American Mathematical Society (Providence, RI, 2007), 247–256. http://www.uni-math.gwdg.de/tschinkel/gauss-dirichlet/stark.pdf.Google Scholar
Stopple, J., Notes on the Deuring–Heilbronn phenomenon. Not. AMS
53(8) 2006, 864–875,http://www.ams.org/notices/200608/fea-stopple.pdf.Google Scholar
Tatuzawa, T., On a theorem of Siegel. Jpn. J. Math.
21
1951, 163–178,http://www.jstage.jst.go.jp/article/jjm1924/21/0/21_0_163/_pdf.Google Scholar
Templier, N., A nonsplit sum of coefficients of modular forms. Duke. Math. J.
157(1) 2011, 109–165, doi:10.1215/00127094-2011-003.Google Scholar
Templier, N. and Tsimerman, J., Non-split sums of coefficients of GL (2)-automorphic forms. Israel J. Math.
195(2) 2013, 677–723, doi:10.1007/s11856-012-0112-2.Google Scholar
Tóth, Á., Roots of quadratic congruences. Int. Math. Res. Not. IMRN
2000(14), 719–739, doi:10.1155/S1073792800000404.Google Scholar
Waldspurger, J.-L., Correspondance de Shimura (French) [The Shimura correspondence]. J. Math. Pures Appl.
59(1) 1980, 1–132. J.-L. Waldspurger, Sur les coefficients de Fourier des formes modulaires de poids demi-entier (French) [On the Fourier coefficients of modular forms of half-integral weight]. J. Math. Pures Appl.
60(1) (1981), 375–484.Google Scholar
Watkins, M., Class numbers of imaginary quadratic fields. Math. Comput.
73(246) 2004, 907–938, doi:10.1090/S0025-5718-03-01517-5.Google Scholar
Watkins, M., A spectral proof of class number one. Math. Z. (to appear), doi:10.1007/s00209-018-2183-1.Google Scholar
Weil, A., Über die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen (German) [On Dirichlet series satisfying functional equations]. Math. Ann.
168
1967, 149–156,http://eudml.org/doc/161499.Google Scholar