Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T07:22:31.397Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain subgroups of free products

Published online by Cambridge University Press:  26 February 2010

D. E. Cohen
D. E. Cohen
Affiliation:
Birmingham University.
Get access

Extract

Let G1,… Gn be groups, let *Gi be their free product, and let ´ Gi be their direct product. A homomorphism 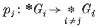may be defined by requiring it to be trivial on Gj and the identity on Gi for i ¹ j. Let [G1 … Gn] = Çker pj. P. J. Hilton [2] proves that [G1, …, Gn] is a free group, and, if HiÌGi, i = 1, …, n, that [H1,… Hn] is a free factor of [G1 … Gn]. He asks whether, if Hλi Ì Gi, λ = 1, …, k, i = 1, …, n, and Hλ = [Hλ1, …, Hλn] the group generated by the Hλ is a free factor of [G1, …, Gn].

Type
Research Article
Information
Mathematika , Volume 7 , Issue 2 , December 1960 , pp. 117 - 124
Copyright
Copyright © University College London 1960

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

011.Gruenberg, K. W., “Residual properties of infinite soluble groups”, Proc. London Math. Soc. (3), 7 (1957), 29–62.CrossRefGoogle Scholar
2.Hilton, P. J., “Remark on free products of groups”, Trans. Amer. Math. Soc. (to appear).Google Scholar
3.Weir, A. J., “The Reidemeister-Schreier and Kuroš subgroup theorems”, Mathematika, 3 (1956), 47–55.CrossRefGoogle Scholar