Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T17:49:59.452Z Has data issue: false hasContentIssue false
  • English
  • Français

BRASCAMP–LIEB INEQUALITY AND QUANTITATIVE VERSIONS OF HELLY’S THEOREM

Part of: Inequalities Normed linear spaces and Banach spaces; Banach lattices General convexity

Published online by Cambridge University Press:  07 December 2016

Silouanos Brazitikos
Silouanos Brazitikos*
Affiliation:
Department of Mathematics, University of Athens, Panepistimioupolis 157-84, Athens, Greece email [email protected]
Get access

Abstract

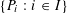We provide new quantitative versions of Helly’s theorem. For example, we show that for every family $\{P_{i}:i\in I\}$ of closed half-spaces in 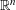$\mathbb{R}^{n}$ such that 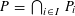$P=\bigcap _{i\in I}P_{i}$ has positive volume, there exist 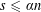$s\leqslant \unicode[STIX]{x1D6FC}n$ and 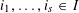$i_{1},\ldots ,i_{s}\in I$ such that

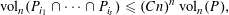$$\begin{eqnarray}\operatorname{vol}_{n}(P_{i_{1}}\cap \cdots \cap P_{i_{s}})\leqslant (Cn)^{n}\operatorname{vol}_{n}(P),\end{eqnarray}$$
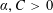where $\unicode[STIX]{x1D6FC},C>0$ are absolute constants. These results complement and improve previous work of Bárány et al and Naszódi. Our method combines the work of Srivastava on approximate John’s decompositions with few vectors, a new estimate on the corresponding constant in the Brascamp–Lieb inequality and an appropriate variant of Ball’s proof of the reverse isoperimetric inequality.

MSC classification

Primary: 26D15: Inequalities for sums, series and integrals
Secondary: 52A23: Asymptotic theory of convex bodies 52A35: Helly-type theorems and geometric transversal theory 46B06: Asymptotic theory of Banach spaces
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 272 - 291
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amenta, N., De Loera, J. A. and Soberón, P., Helly’s theorem: new variations and applications. Preprint, 2016, arXiv:1508.07606v2.CrossRefGoogle Scholar
Artstein-Avidan, S., Giannopoulos, A. and Milman, V. D., Asymptotic Geometric Analysis, Part I (Mathematical Surveys and Monographs 202 ), American Mathematical Society (Providence, RI, 2015).Google Scholar
Ball, K. M., Volumes of sections of cubes and related problems. In Geometric Aspects of Functional Analysis (1987–88) (Lecture Notes in Mathematics 1376 ), Springer (Berlin, 1989), 251–260.CrossRefGoogle Scholar
Ball, K. M., Volume ratios and a reverse isoperimetric inequality. J. Lond. Math. Soc. (2) 44 1991, 351–359.Google Scholar
Ball, K. M. and Pajor, A., Convex bodies with few faces. Proc. Amer. Math. Soc. 110(1) 1990, 225–231.CrossRefGoogle Scholar
Bárány, I., Katchalski, M. and Pach, J., Quantitative Helly-type theorems. Proc. Amer. Math. Soc. 86 1982, 109–114.Google Scholar
Bárány, I., Katchalski, M. and Pach, J., Helly’s theorem with volumes. Amer. Math. Monthly 91 1984, 362–365.Google Scholar
Barvinok, A., Thrifty approximations of convex bodies by polytopes. Int. Math. Res. Not. IMRN 2014(16) 2014, 4341–4356.CrossRefGoogle Scholar
Batson, J., Spielman, D. and Srivastava, N., Twice-Ramanujan sparsifiers. In STOC’09: Proc. 2009 ACM Int. Sympos. Theory of Computing, ACM (New York, 2009), 255–262.Google Scholar
Bourgain, J. and Milman, V. D., New volume ratio properties for convex symmetric bodies in ℝ n . Invent. Math. 88 1987, 319–340.Google Scholar
Brascamp, H. J. and Lieb, E. H., Best constants in Young’s inequality, its converse and its generalization to more than three functions. Adv. Math. 20 1976, 151–173.CrossRefGoogle Scholar
Bronstein, E. M., Approximation of convex sets by polytopes. J. Math. Sci. 153 2008, 727–762.Google Scholar
Carl, B. and Pajor, A., Gelfand numbers of operators with values in a Hilbert space. Invent. Math. 94 1988, 479–504.Google Scholar
Danzer, L., Grünbaum, B. and Klee, V., Helly’s Theorem and its Relatives (Proceedings of Symposia in Pure Mathematics VII ), American Mathematical Society (Providence, RI, 1963), 101–180.Google Scholar
De Loera, J. A., La Haye, R. N., Rolnick, D. and Soberón, P., Quantitative Tverberg, Helly & Carathéodory theorems. Preprint.Google Scholar
Dvoretzky, A. and Rogers, C. A., Absolute and unconditional convergence in normed linear spaces. Proc. Natl. Acad. Sci. USA 36 1950, 192–197.Google Scholar
Eckhoff, J., Helly, Radon, and Carathéodory type theorems. In Handbook of Convex Geometry, Vols. A, B, North-Holland (Amsterdam, 1993), 389–448.Google Scholar
Friedland, O. and Youssef, P., Approximating matrices and convex bodies through Kadison–Singer. Preprint, arXiv:1605.03861.Google Scholar
Gluskin, E. D., Extremal properties of orthogonal parallelepipeds and their applications to the geometry of Banach spaces. Mat. Sb. (N. S.) 136 1988, 85–96.Google Scholar
Gluskin, E. D. and Litvak, A. E., A remark on vertex index of the convex bodies. In Geometric Aspects of Functional Analysis (Lecture Notes in Mathematics 2050 ), Springer (Berlin, 2012), 255–265.Google Scholar
Gordon, Y., Meyer, M. and Reisner, S., Constructing a polytope to approximate a convex body. Geom. Dedicata 57 1995, 217–222.Google Scholar
Gordon, Y., Reisner, S. and Schütt, C., Umbrellas and polytopal approximation of the Euclidean ball. J. Approx. Theory 90 1997, 9–22.Google Scholar
Gruber, P. M., Aspects of approximation of convex bodies. In Handbook of Convex Geometry, Vols. A, B, North-Holland (Amsterdam, 1993), 319–345.Google Scholar
John, F., Extremum problems with inequalities as subsidiary conditions. In Courant Anniversary Volume, Interscience (New York, 1948), 187–204.Google Scholar
Marcus, A. W., Spielman, D. A. and Srivastava, N., Interlacing families II: mixed characteristic polynomials and the Kadison–Singer problem. Ann. of Math. (2) 182(1) 2015, 327–350.Google Scholar
Naszódi, M., Proof of a conjecture of Bárány, Katchalski and Pach. Discrete Comput. Geom. 55 2016, 243–248.CrossRefGoogle Scholar
Pelczynski, A. and Szarek, S. J., On parallelepipeds of minimal volume containing a convex symmetric body in ℝ n . Math. Proc. Cambridge Philos. Soc. 109 1991, 125–148.CrossRefGoogle Scholar
Rudelson, M., Contact points of convex bodies. Israel J. Math. 101 1997, 93–124.CrossRefGoogle Scholar
Schneider, R., Convex Bodies: The Brunn–Minkowski Theory, 2nd expanded edn. (Encyclopedia of Mathematics and its Applications 151 ), Cambridge University Press (Cambridge, 2014).Google Scholar
Srivastava, N., On contact points of convex bodies. In Geometric Aspects of Functional Analysis (Lecture Notes in Mathematics 2050 ), Springer (Heidelberg, 2012), 393–412.Google Scholar