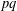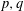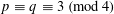Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dummit, David S.
Dummit, Evan P.
and
Kisilevsky, Hershy
2016.
Characterizations of quadratic, cubic, and quartic residue matrices.
Journal of Number Theory,
Vol. 168,
Issue. ,
p.
167.
Lemke Oliver, Robert J.
and
Soundararajan, Kannan
2016.
Unexpected biases in the distribution of consecutive primes.
Proceedings of the National Academy of Sciences,
Vol. 113,
Issue. 31,
Hough, Patrick
2017.
A lower bound for biases amongst products of two primes.
Research in Number Theory,
Vol. 3,
Issue. 1,
Meng, Xianchang
2018.
LARGE BIAS FOR INTEGERS WITH PRIME FACTORS IN ARITHMETIC PROGRESSIONS.
Mathematika,
Vol. 64,
Issue. 1,
p.
237.
Dummit, David S.
and
Voight, John
2018.
The 2‐Selmer group of a number field and heuristics for narrow class groups and signature ranks of units.
Proceedings of the London Mathematical Society,
Vol. 117,
Issue. 4,
p.
682.
Saad Eddin, Sumaia
and
Suzuki, Yuta
2020.
On the distribution of products of two primes.
Journal of Number Theory,
Vol. 214,
Issue. ,
p.
100.
Devin, Lucile
and
Meng, Xianchang
2021.
Chebyshev's bias for products of irreducible polynomials.
Advances in Mathematics,
Vol. 392,
Issue. ,
p.
108040.
Wannes, Walid
2022.
Large Bias Amongst Products of Two Primes.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 45,
Issue. 2,
p.
623.
Gorodetsky, Ofir
2023.
Sums of two squares are strongly biased towards quadratic residues.
Algebra & Number Theory,
Vol. 17,
Issue. 3,
p.
775.
Fiorilli, Daniel
and
Jouve, Florent
2024.
DISTRIBUTION OF FROBENIUS ELEMENTS IN FAMILIES OF GALOIS EXTENSIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 23,
Issue. 3,
p.
1169.
Wannes, Walid
2024.
Biases amongst products of two Beatty primes in arithmetic progressions.
Indian Journal of Pure and Applied Mathematics,
Martin, Greg
Yang, Pu Justin Scarfy
Bahrini, Aram
Bajpai, Prajeet
Benli̇, Kübra
Downey, Jenna
Li, Yuan Yuan
Liang, Xiaoxuan
Parvardi, Amir
Simpson, Reginald
White, Ethan Patrick
and
Yip, Chi Hoi
2025.
An annotated bibliography for comparative prime number theory.
Expositiones Mathematicae,
Vol. 43,
Issue. 3,
p.
125644.