Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T01:55:18.118Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXPLICIT TWO-SOURCE EXTRACTOR WITH MIN-ENTROPY RATE NEAR 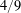$4/9$

Part of: Mathematics education -Computer science Numerical methods in Fourier analysis Combinatorics, graph theory, probability theory, statistics

Published online by Cambridge University Press:  24 July 2019

Mark Lewko
Mark Lewko*
Affiliation:
New York, NY 10017, U.S.A. email [email protected]
Get access

Abstract

In 2005 Bourgain gave the first explicit construction of a two-source extractor family with min-entropy rate less than 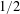$1/2$. His approach combined Fourier analysis with innovative but inefficient tools from arithmetic combinatorics and yielded an unspecified min-entropy rate which was greater than 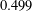$0.499$. This remained essentially the state of the art until a 2015 breakthrough by Chattopadhyay and Zuckerman in which they gave an alternative approach which produced extractors with arbitrarily small min-entropy rate. In the current work, we revisit the Fourier analytic approach. We give an improved analysis of one of Bourgain’s extractors which shows that it in fact extracts from sources with min-entropy rate near 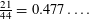$\frac{21}{44}=0.477\ldots .$ Moreover, we construct a variant of this extractor which we show extracts from sources with min-entropy rate near 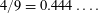$4/9=0.444\ldots .$ While this min-entropy rate is inferior to Chattopadhyay and Zuckerman’s construction, our extractors have the advantage of exponential small error, which is important in some applications. The key ingredient in these arguments is recent progress connected to the restriction theory of the finite field paraboloid by Rudnev and Shkredov. This in turn relies on a Rudnev’s point–plane incidence estimate, which in turn relies on Kollár’s generalization of the Guth–Katz incidence theorem.

MSC classification

Primary: 65T50: Discrete and fast Fourier transforms 97K20: Combinatorics 97P20: Theory of computer science
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 950 - 957
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourgain, J., More on the sum-product phenomenon in prime fields and its applications. Int. J. Number Theory 1(1) 2005, 1–32.10.1142/S1793042105000108Google Scholar
Bourgain, J., Katz, N. and Tao, T., A sum-product estimate in finite fields, and applications. Geom. Funct. Anal. 14(1) 2004, 27–57.10.1007/s00039-004-0451-1Google Scholar
Bourgain, J. and Garaev, M. Z., On a variant of sum-product estimates and explicit exponential sum bounds in prime fields. Math. Proc. Cambridge Philos. Soc. 146 2009, 1–21.10.1017/S0305004108001230Google Scholar
Chattopadhyay, E. and Zuckerman, D., Explicit two-source extractors and resilient functions. Proc. Symp. on the Theory of Computing (STOC 2016), ACM (2016), 670–683.Google Scholar
Guth, L. and Katz, N. H., On the Erdös distinct distance problem in the plane. Ann. of Math. (2) 181(1) 2015, 155–190.10.4007/annals.2015.181.1.2Google Scholar
Hegyvari, N. and Hennecart, F., Explicit constructions of extractors and expanders. Acta Arith. 140 2009, 233–249.10.4064/aa140-3-2Google Scholar
Helfgott, H. and Rudnev, M., An explicit incidence theorem in F p . Mathematika 57 2011, 135–156.10.1112/S0025579310001208Google Scholar
Iosevich, A., Koh, D. and Lewko, M., Finite field restriction estimates for the paraboloid in high even dimensions. Preprint, 2017, arXiv:1712.05549v1.Google Scholar
Jones, T., Further improvements to incidence and Beck-type bounds over prime finite fields. Preprint, 2012, arXiv:1206.4517.Google Scholar
Kollár, J., Szemerédi–Trotter-type theorems in dimension 3. Adv. Math. 271 2015, 30–61.10.1016/j.aim.2014.11.014Google Scholar
Lewko, A. and Lewko, M., Endpoint restriction estimates for the paraboloid over finite fields. Proc. Amer. Math. Soc. 140 2012, 2013–2028.10.1090/S0002-9939-2011-11444-8Google Scholar
Lewko, M., Finite field restriction estimates based on Kakeya maximal operator estimates. J. Eur. Math. Soc. (JEMS), to appear. Preprint, 2014, arXiv:1401.8011v5.Google Scholar
Lewko, M., New restriction estimates for the 3-d paraboloid over finite fields. Adv. Math. 270 2015, 457–479.10.1016/j.aim.2014.11.008Google Scholar
Lewko, M., Counting rectangles and an improved restriction estimate for the paraboloid in $F_{p}^{3}$ . Preprint, 2019, arXiv:1901.10085.Google Scholar
Mockenhaupt, G. and Tao, T., Restriction and Kakeya phenomena for finite fields. Duke Math. J. 121(1) 2004, 35–74.Google Scholar
Rao, A., An exposition of Bourgain’s 2-source extractor,http://homes.cs.washington.edu/∼anuprao/pubs/bourgain.pdf.Google Scholar
Rudnev, M., On the number of incidences between planes and points in three dimensions. Combinatorica 38(1) 2018, 219–254.10.1007/s00493-016-3329-6Google Scholar
Rudnev, M. and Shkredov, I., On the restriction problem for the discrete paraboloid in lower dimension. Preprint, 2018, arXiv:1803.11035.10.1016/j.aim.2018.10.002Google Scholar
Stevens, S. and de Zeeuw, F., An improved point-line incidence bound over arbitrary fields. Bull. Lond. Math. Soc. 49 2017, 842–858.10.1112/blms.12077Google Scholar
Tao, T. and Vu, V., Additive Combinatorics, Cambridge University Press (Cambridge, 2006).10.1017/CBO9780511755149Google Scholar
von Neumann, J., Various techniques used in connection with random digits. In Monte Carlo Method (National Bureau of Standards Applied Mathematics Series 12 ) (eds Householder, A. S., Forsythe, G. E. and Germond, H. H.), U.S. Government Printing Office (Washington, DC, 1951), 36–38.Google Scholar