Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cilleruelo, Javier
Garaev, Moubariz Z.
Ostafe, Alina
and
Shparlinski, Igor E.
2012.
On the concentration of points of polynomial maps and applications.
Mathematische Zeitschrift,
Vol. 272,
Issue. 3-4,
p.
825.
Hegyvári, Norbert
and
Hennecart, François
2013.
Conditional expanding bounds for two-variable functions over prime fields.
European Journal of Combinatorics,
Vol. 34,
Issue. 8,
p.
1365.
Bibak, Khodakhast
2013.
Number Theory and Related Fields.
Vol. 43,
Issue. ,
p.
99.
2013.
Handbook of Finite Fields.
p.
777.
Grosu, Codruţ
2014.
Fp is locally like ℂ.
Journal of the London Mathematical Society,
Vol. 89,
Issue. 3,
p.
724.
Iosevich, Alex
Rudnev, Misha
and
Zhai, Yujia
2015.
Areas of triangles and Beck’s theorem in planes over finite fields.
Combinatorica,
Vol. 35,
Issue. 3,
p.
295.
Murphy, Brendan
Roche-Newton, Oliver
and
Shkredov, Ilya
2015.
Variations on the Sum-Product Problem.
SIAM Journal on Discrete Mathematics,
Vol. 29,
Issue. 1,
p.
514.
Lewko, Mark
2015.
New restriction estimates for the 3-d paraboloid over finite fields.
Advances in Mathematics,
Vol. 270,
Issue. ,
p.
457.
Jones, Timothy G.F.
2016.
An improved incidence bound for fields of prime order.
European Journal of Combinatorics,
Vol. 52,
Issue. ,
p.
136.
Hanson, Brandon
Lund, Ben
and
Roche-Newton, Oliver
2016.
On distinct perpendicular bisectors and pinned distances in finite fields.
Finite Fields and Their Applications,
Vol. 37,
Issue. ,
p.
240.
Yazici, Esen Aksoy
Murphy, Brendan
Rudnev, Misha
and
Shkredov, Ilya
2016.
Growth Estimates in Positive Characteristic via Collisions.
International Mathematics Research Notices,
p.
rnw206.
Pham, Thang
Tait, Michael
Timmons, Craig
and
Vinh, Le Anh
2017.
A Szemerédi–Trotter type theorem, sum-product estimates in finite quasifields, and related results.
Journal of Combinatorial Theory, Series A,
Vol. 147,
Issue. ,
p.
55.
Ham, Le Quang
Thang, Pham Van
and
Vinh, Le Anh
2017.
Conditional expanding bounds for two-variable functions over finite valuation rings.
European Journal of Combinatorics,
Vol. 60,
Issue. ,
p.
114.
Stevens, Sophie
and
de Zeeuw, Frank
2017.
An improved point-line incidence bound over arbitrary fields.
Bulletin of the London Mathematical Society,
Vol. 49,
Issue. 5,
p.
842.
Petridis, Giorgis
2017.
Pinned algebraic distances determined by Cartesian products in 𝔽_{𝕡}².
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 11,
p.
4639.
Petridis, Giorgis
and
Shparlinski, Igor E.
2019.
Bounds of Trilinear and Quadrilinear Exponential Sums.
Journal d'Analyse Mathématique,
Vol. 138,
Issue. 2,
p.
613.
Lewko, Mark
2019.
AN EXPLICIT TWO‐SOURCE EXTRACTOR WITH MIN‐ENTROPY RATE NEAR.
Mathematika,
Vol. 65,
Issue. 4,
p.
950.
Mohammadi, Ali
Pham, Thang
and
Warren, Audie
2023.
A point-conic incidence bound and applications over Fp.
European Journal of Combinatorics,
Vol. 107,
Issue. ,
p.
103596.
Iosevich, Alex
Pham, Thang
Senger, Steven
and
Tait, Michael
2024.
Improved incidence bounds over arbitrary finite fields via the VC-dimension theory.
European Journal of Combinatorics,
Vol. 118,
Issue. ,
p.
103928.


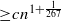 lines, where
lines, where 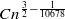 , where
, where 