Article contents
An elementary derivation of certain homological inequalities
Published online by Cambridge University Press: 26 February 2010
Extract
Let R be a ring, not necessarily commutative, with an identity element, and let A be a left R-module. We shall describe this situation by writing (RA). If
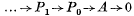
is an exact sequence of left. R-modules and R-homomorphisms in which each Pi (i ≥ 0) is R-projective, then the sequence
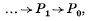
which we denote by P, is called an R-projective resolution of A. Suppose now that A is non-trivial; if Pi = 0 when i > n and if there are no R-projective resolutions of A containing fewer non-zero terms, then A is said to have left projective (or homological) dimension n, and we write 1.dim RA = n. If no finite resolutions of this type exist, we write l.dim RA = ∞. As a convention, we put l.dim R0 = −1. If M denotes a variable left R-module, then 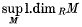 is called the left global dimension of the ring R and is denoted by l.gl. dim R. It is well known that l.dim RA < n if and only if
is called the left global dimension of the ring R and is denoted by l.gl. dim R. It is well known that l.dim RA < n if and only if 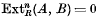 for all left R-modules B and that l.gl.dim R < m if and only if
for all left R-modules B and that l.gl.dim R < m if and only if 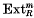 regarded as a functor of left R-modules, takes only null values.
regarded as a functor of left R-modules, takes only null values.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1963
References
- 3
- Cited by


