Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T02:43:24.100Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIVALENT FUNCTIONS AND RADIAL GROWTH

Part of: Geometric function theory

Published online by Cambridge University Press:  16 January 2015

J. B. Twomey
J. B. Twomey*
Affiliation:
Department of Mathematics, University College Cork, Western Road Cork, Ireland email [email protected]
Get access

Abstract

We address a question raised by Anderson, Hayman and Pommerenke relating to a classical result on univalent functions 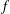$f$ in the unit disc due to Spencer, and involving the size of the set of 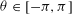${\it\theta}\in [-{\it\pi},{\it\pi}]$ for which we have 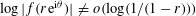$\log |f(r\text{e}^{\text{i}{\it\theta}})|\neq o(\log (1/(1-r)))$ as 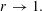$r\rightarrow 1.$ An answer is given in terms of a certain generalized capacity, and also in terms of Hausdorff measure. Further results regarding the radial growth of univalent functions are also established, and some examples are constructed which relate to the sharpness of these results.

MSC classification

Primary: 30C35: General theory of conformal mappings
Type
Research Article
Information
Mathematika , Volume 61 , Issue 3 , September 2015 , pp. 531 - 546
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. M., Hayman, W. K. and Pommerenke, Ch., The radial growth of univalent functions. J. Comput. Appl. Math. 171(1–2) 2004, 27–37.CrossRefGoogle Scholar
Beurling, A., Ensembles exceptionels. Acta Math. 72 1940, 1–13.CrossRefGoogle Scholar
Borichev, A., Lyubarskii, Yu., Malinnikova, E. and Thomas, P., Radial growth of functions in the Korenblum space. Algebra i Analiz 21(6) 2009, 47–65 ; Engl. Transl. St. Petersburg Math. J. 21(6) (2010), 877–891.Google Scholar
Carleson, L., Selected Problems on Exceptional Sets, Van Nostrand (Princeton, New Jersey, 1967).Google Scholar
Duren, P. L., Univalent Functions, Springer (New York, 1983).Google Scholar
Hayman, W. K., Multivalent Functions, 2nd edn edn., Cambridge University Press (Cambridge, 1994).CrossRefGoogle Scholar
Lyubarskii, Yu. and Malinnikova, E., Radial oscillation of harmonic functions in the Korenblum class. Bull. Lond. Math. Soc. 44 2012, 68–84.CrossRefGoogle Scholar
Pommerenke, Ch., Univalent Functions, Vandenhoeck and Ruprecht (Göttingen, 1975).Google Scholar
Pommerenke, Ch., Boundary Behaviour of Conformal Maps (Grundlehren der Mathematischen Wissenschaften 299), Springer (Berlin, 1991).Google Scholar
Spencer, D. C., On finitely mean-valent functions II. Trans. Amer. Math. Soc. 48 1940, 418–435.CrossRefGoogle Scholar
Twomey, J. B., Radial and tangential growth of close-to-convex functions. Proc. Edinb. Math. Soc. (2) 48(1) 2005, 143–152.Google Scholar
Zygmund, A., Trigonometric Series, Vols. I and II, Cambridge University Press (New York, 1959).Google Scholar