Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DENG, JUAN
and
XI, LIFENG
2016.
GAP SEQUENCES OF GRAPH-DIRECTED SETS.
Fractals,
Vol. 24,
Issue. 03,
p.
1650036.
Zou, Yuru
Wang, Lijin
Lu, Jian
and
Baker, Simon
2016.
ON SMALL BASES FOR WHICH 1 HAS COUNTABLY MANY EXPANSIONS.
Mathematika,
Vol. 62,
Issue. 2,
p.
362.
Zou, Yuru
Li, Wenxia
and
Lu, Jian
2016.
On the cardinality of β-expansions of some numbers.
International Journal of Number Theory,
Vol. 12,
Issue. 06,
p.
1497.
LU, JIAN
TAN, BO
and
ZOU, YURU
2018.
INTERSECTIONS OF TRANSLATION OF A CLASS OF SIERPINSKI CARPETS.
Fractals,
Vol. 26,
Issue. 03,
p.
1850034.
Chen, Xiu
Jiang, Kan
and
Li, Wenxia
2019.
Estimating the Hausdorff dimensions of univoque sets for self-similar sets.
Indagationes Mathematicae,
Vol. 30,
Issue. 5,
p.
862.
Dajani, Karma
Jiang, Kan
Kong, Derong
and
Li, Wenxia
2019.
Multiple expansions of real numbers with digits set
$$\left\{ 0,1,q\right\} $$
0
,
1
,
q
.
Mathematische Zeitschrift,
Vol. 291,
Issue. 3-4,
p.
1605.
Kong, D.
and
Yao, Y.
2021.
On a kind of self-similar sets with complete overlaps.
Acta Mathematica Hungarica,
Vol. 163,
Issue. 2,
p.
601.
Dajani, Karma
Jiang, Kan
Kong, Derong
Li, Wenxia
and
Xi, Lifeng
2021.
Multiple codings of self-similar sets with overlaps.
Advances in Applied Mathematics,
Vol. 124,
Issue. ,
p.
102146.


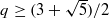 .
.