Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T09:04:39.054Z Has data issue: false hasContentIssue false
  • English
  • Français

THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS

Part of: Sequences and sets Combinatorics Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  23 July 2019

Christoph Aistleitner ,
Thomas Lachmann  and
Niclas Technau
Christoph Aistleitner
Affiliation:
Institute for Analysis and Number Theory, University of Technology Graz, Steyrergasse 30, 8010 Graz, Austria email [email protected]
Thomas Lachmann
Affiliation:
Institute for Analysis and Number Theory, University of Technology Graz, Steyrergasse 30, 8010 Graz, Austria email [email protected]
Niclas Technau
Affiliation:
Raymond and Beverly Sackler School of Mathematical Sciences, Tel Aviv University, 69978 Tel Aviv, Israel email [email protected]
Get access

Abstract

We consider sequences of the form 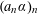$(a_{n}\unicode[STIX]{x1D6FC})_{n}$ mod 1, where 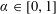$\unicode[STIX]{x1D6FC}\in [0,1]$ and where 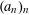$(a_{n})_{n}$ is a strictly increasing sequence of positive integers. If the asymptotic distribution of the pair correlations of this sequence follows the Poissonian model for almost all $\unicode[STIX]{x1D6FC}$ in the sense of Lebesgue measure, we say that 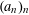$(a_{n})_{n}$ has the metric pair correlation property. Recent research has revealed a connection between the metric theory of pair correlations of such sequences, and the additive energy of truncations of 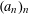$(a_{n})_{n}$. Bloom, Chow, Gafni and Walker speculated that there might be a convergence/divergence criterion which fully characterizes the metric pair correlation property in terms of the additive energy, similar to Khintchine’s criterion in the metric theory of Diophantine approximation. In the present paper we give a negative answer to such speculations, by showing that such a criterion does not exist. To this end, we construct a sequence 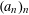$(a_{n})_{n}$ having large additive energy which, however, maintains the metric pair correlation property.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity 11K60: Diophantine approximation
Secondary: 05A18: Partitions of sets 11B25: Arithmetic progressions 11K06: General theory of distribution modulo $1$
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 929 - 949
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aistleitner, C., Metric number theory, lacunary series and systems of dilated functions. In Uniform Distribution and Quasi-Monte Carlo Methods (Radon Series on Computational and Applied Mathematics 15 ), De Gruyter (Berlin, 2014), 1–16.Google Scholar
Aistleitner, C., Larcher, G. and Lewko, M., Additive energy and the Hausdorff dimension of the exceptional set in metric pair correlation problems. With an appendix by Jean Bourgain. Israel J. Math. 222(1) 2017, 463–485.10.1007/s11856-017-1597-5Google Scholar
Berry, M. and Tabor, M., Level clustering in the regular spectrum. Proc. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 356(1686) 1977, 375–394.10.1098/rspa.1977.0140Google Scholar
Bloom, T. F., Chow, S., Gafni, A. and Walker, A., Additive energy and the metric Poissonian property. Mathematika 64(3) 2018, 679–700.10.1112/S0025579318000207Google Scholar
Bloom, T. F. and Walker, A., GCD sums and sum-product estimates. Preprint, 2018,arXiv:1806.07849.Google Scholar
Bugeaud, Y., Approximation by Algebraic Numbers (Cambridge Tracts in Mathematics 160 ), Cambridge University Press (Cambridge, 2004).10.1017/CBO9780511542886Google Scholar
Chow, S., Bohr sets and multiplicative Diophantine approximation. Duke Math. J. 167(9) 2018, 1623–1642.10.1215/00127094-2018-0001Google Scholar
Harman, G., Metric Number Theory (London Mathematical Society Monographs. New Series 18 ), Clarendon Press (Oxford, 1998).Google Scholar
Heath-Brown, D. R., Pair correlation for fractional parts of 𝛼n 2 . Math. Proc. Cambridge Philos. Soc. 148(3) 2010, 385–407.10.1017/S0305004109990466Google Scholar
Lachmann, T. and Technau, N., On exceptional sets in the metric Poissonian pair correlations problem. Monatsh. Math. 189 2019, 137–156.10.1007/s00605-018-1199-2Google Scholar
Marklof, J., The Berry–Tabor conjecture. In European Congress of Mathematics, Vol. II (Barcelona, 2000) (Progress in Mathematics 202 ), Birkhäuser (Basel, 2001), 421–427.10.1007/978-3-0348-8266-8_36Google Scholar
Rudnick, Z. and Sarnak, P., The pair correlation function of fractional parts of polynomials. Comm. Math. Phys. 194(1) 1998, 61–70.10.1007/s002200050348Google Scholar
Rudnick, Z., Sarnak, P. and Zaharescu, A., The distribution of spacings between the fractional parts of n 2𝛼. Invent. Math. 145(1) 2001, 37–57.10.1007/s002220100141Google Scholar
Rudnick, Z. and Zaharescu, A., The distribution of spacings between fractional parts of lacunary sequences. Forum Math. 14(5) 2002, 691–712.10.1515/form.2002.030Google Scholar
Truelsen, J. L., Divisor problems and the pair correlation for the fractional parts of n 2𝛼. Int. Math. Res. Not. IMRN 2010(16) 2010, 3144–3183.Google Scholar
Walker, A., The primes are not metric Poissonian. Mathematika 64(1) 2018, 230–236.10.1112/S002557931700050XGoogle Scholar