Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Actor, A
and
Bender, I
1996.
The zeta function constructed from the zeros of the Bessel function.
Journal of Physics A: Mathematical and General,
Vol. 29,
Issue. 20,
p.
6555.
Komarov, M. A.
2020.
Note on power sums of the zeros of certain Laguerre and Bessel polynomials.
Integral Transforms and Special Functions,
Vol. 31,
Issue. 7,
p.
562.


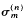 be the sum of the
be the sum of the