Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T13:33:06.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Sums of k-th powers in number fields

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  26 February 2010

Morley Davidson
Morley Davidson
Affiliation:
Dept. of Math. and C.S., Kent State University, Kent, Ohio 44242, U.S.A.
Get access

Extract

As usual in Waring's problem, we let G(k) be the least number s such that all sufficiently large natural numbers can be written as the sum of s or fewer k-th powers of positive integers. Hardy and Littlewood gave the first general upper bound, G(k)≤(k − 2)2k − 1 + 5. Later [4], they reduced this to order k2 by first constructing an auxiliary set of natural numbers below x which are sums of sk-th powers, of cardinality 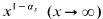with 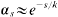for large k. The argument, which is brief and elementary (see [15, Chapter 6]), is now referred to by R. C. Vaughan's term “diminishing ranges”, since the k-th powers are taken from intervals of decreasing lengths. This idea of choosing the variables from restricted ranges was refined by Vinogradov, whose application to exponential sum estimates gave 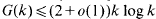for large k (see [18]). The recent iterative method of Vaughan and Wooley [16, 19, 21], which halves Vinogradov's bound, may be viewed as an evolved diminishing ranges argument, producing an auxiliary set with .

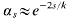MSC classification

Secondary: 11P05: Waring's problem and variants
Type
Research Article
Information
Mathematika , Volume 45 , Issue 2 , December 1998 , pp. 359 - 370
Copyright
Copyright © University College London 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Davidson, M.. On Waring's problem in number fields. To appear in Jour. London Math. Soc.Google Scholar
2.Davidson, M.. On Siegel's conjecture in Waring's problem. Forthcoming.Google Scholar
3.Eda, Y.. On Waring's problem in an algebraic number field. Rev. Colombiana Math. 9 (1975), 2973.Google Scholar
4.Hardy, G. H. and Littlewood, J. E.. Some problems in "Partitio Numerorum". VI: Further researches in Waring's problem. Math. Z., 23 (1925), 437.Google Scholar
5.Körner, O.. Über die Waringsche Problem in algebraischen Zahlkőrpern. Math. Ann., 144 (1961), 224238.CrossRefGoogle Scholar
6.Körner, O.. Über Mittelwerte trigonometrischer Summen und ihre Anwcndung in Algebraischen Zahlkörpern. Math. Ann., 147 (1962), 205239.CrossRefGoogle Scholar
7.Mitsui, T.. On the Goldbach problem in an algebraic number field I, II. Jour. Math. Soc. Japan. 13 (1960), 290–372.Google Scholar
8.Mordell, L. J.. On the representation of algebraic numbers as a sum of four squares. Proc. Cambridge Phil. Soc, 20 (1921), 250–256.Google Scholar
9.Siegel, C. L.. Darstellung total positiver Zahlcn durch Quadrate. Math. Zeit., 10 (1921), 246 215; > Ges. Abh. I, 41–16 (Springer, 1966).CrossRefGoogle Scholar
10.Siegel, C. L.. Generalization of Waring's problem to algebraic number fields. American J. of Math., 66 (1944), 122136; > Ges. Abh. II, 406420. (Springer, 1966).CrossRefGoogle Scholar
11.Siegel, C. L.. Sums of m-th powers of algebraic integers. Ann. Math., 46 (1945), 313339; > Ges. Abh. Ill, 12–38 (Springer, 1966).CrossRefGoogle Scholar
12.Stemmler, R. M.. On the easier Waring problem in algebraic number fields. Ada Arith., 6 (1961), 447–468.CrossRefGoogle Scholar
13.Tatuzawa, T.. On the Waring problem in an algebraic number field. Journ. Math. Soc. Japan, 10 (1958), 322341.Google Scholar
14.Tatuzawa, T.. On Waring's problem in algebraic number fields. Ada Arith., 24 (1973), 3760.CrossRefGoogle Scholar
15.Vaughan, R. C.. The Hardv-Littlewood method (Cambridge University Press, Cambridge, 1981).Google ScholarPubMed
16.Vaughan, R. C.. A new iterative method in Waring's problem. Ada Math., 162 (1989), 171.Google Scholar
17.Vinogradov, I. M.. the method of trigonometrical sums in the theorv of numbers, Trav. Inst. Steklov, 23 (1947). Translated from Russian and revised by A. Davenport and K. Roth (1954, New York: Interscience).Google Scholar
18.Vinogradov, I. M.. On the question of the upper bound for G(n) (in Russian). Izv. Akad. Nauk., 23 (1959), 637642.Google Scholar
19.Vaughan, R. C. and Wooley, T. D.. Further improvements in Waring's problem. Ada Math. 174 (1995), 147240.Google Scholar
20.Wang, Y.. Diophantine Equations and Inequalities in Algebraic Number Fields (Springer-Verlag. Berlin, Heidelberg, 1991).Google Scholar
21.Wooley, T. D.. Large improvements in Waring's problem. Ann. Math., 135 (1992), 131164.CrossRefGoogle Scholar