Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T08:07:07.814Z Has data issue: false hasContentIssue false
  • English
  • Français

A special triple exponential sum

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  26 February 2010

H.-Q. Liu
H.-Q. Liu
Affiliation:
206-10, Bao Guo St., Harbin, 150066, China.
Get access

Extract

In this short paper, we shall give a new estimate for the exponential sum S(H, M, N), where

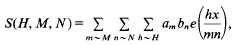
e( ξ,) = exp (2πiξ;) for a real number ξ, am and bn are complex numbers with |am| ≤ 1 and |bn| ≤ l, H, M, N ≤1, , x is a large number, ε is a sufficiently small positive number, and Y ≤ x(½)−ε (h ∼ H means 1≤h/H < 2 and so on). In making application of the Rosser-Iwaniec linear sieve of Iwaniec [6] to find almost primes in short intervals of the type (x − y, x], Halberstam, Heath-Brown and Richert [4] first considered an estimate for S(H, M, N) to the effect that

with MN as large as possible. Later, better estimates were given in Iwaniec and Laborde [7], and Fouvry and Iwaniec [3]. Of course, the most interesting case would be finding P2 numbers in a short interval (x − y, x]. The related estimate of [7] implies that (1) holds provided that

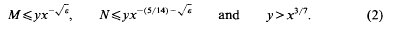
MSC classification

Secondary: 11L07: Estimates on exponential sums
Type
Research Article
Information
Mathematika , Volume 42 , Issue 1 , June 1995 , pp. 137 - 143
Copyright
Copyright © University College London 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, A.. A concise introduction to the theory of numbers (Cambridge Univ. Press, 1984).CrossRefGoogle Scholar
2.Bombieri, E. and Iwaniec, H.. On the order of . Ann. Scuola. Norm. Sup. Pisa, 13 (1986), 449–472.Google Scholar
3.Fouvry, E. and Iwaniec, H.. Exponential sums with monomials. J. Number Theory, 33 (1989), 311–333.CrossRefGoogle Scholar
4.Halberstam, H., Heath-Brown, D. R. and Richert, H.-E.. Almost primes in short intervals. In Recent Progress in Analytic Number Theory, Vol. I, 69–102 (Academic Press, London, 1981).Google Scholar
5.Heath-Brown, D. R., The Pjateckii-Sapiro prime number theorem. J. Number Theory, 16 (1983), 242–266.Google Scholar
6.Iwaniec, H.. A new form of the error term in the linear sieve. Ada Arith., 37 (1980), 307[320.Google Scholar
7.Iwaniec, H. and Laborde, M.. P2 in short intervals. Ann. Inst. Fourier, 31 (1981), 37–56.CrossRefGoogle Scholar