Published online by Cambridge University Press: 26 February 2010
For satellite knots there is a well-known formula which relates the Alexander polynomial of the satellite to those of a companion knot and the corresponding pattern. If &s, &C and &P are the Alexander polynomials of a satellite, companion and pattern respectively then
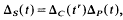
where 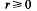 is the linking number of P with a meridian of the companion torus (see [BZ], p. 118). Analogous relationships do not exist for other knot polynomials [MS]. This suggests that the existence of the above formula depends more on the geometry underlying the polynomial than on the geometry of the satellite construction.
is the linking number of P with a meridian of the companion torus (see [BZ], p. 118). Analogous relationships do not exist for other knot polynomials [MS]. This suggests that the existence of the above formula depends more on the geometry underlying the polynomial than on the geometry of the satellite construction.