Article contents
Ramanujan's explicit values for the classical theta-function
Published online by Cambridge University Press: 26 February 2010
Extract
Let
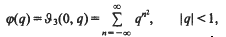
where φ is the notation used by Ramanujan in his notebooks [15], and is the familiar notation of Whittaker and Watson [20, p. 464]. It is well known that [1, p. 102] (with a misprint corrected)
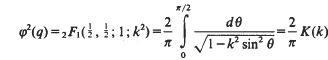
where 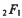 denotes the ordinary or Gaussian hypergeometric function; k, 0 < k < 1, is the modulus; K is the complete elliptic integral of the first kind; and
denotes the ordinary or Gaussian hypergeometric function; k, 0 < k < 1, is the modulus; K is the complete elliptic integral of the first kind; and
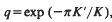
where K′=K(k′) and 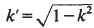 is the complementary modulus. Thus, an evaluation of any one of the functions φ,
is the complementary modulus. Thus, an evaluation of any one of the functions φ, 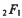 , or K yields an evaluation of the other two functions. However, such evaluations may not be very explicit. For example, if K(k) is known for a certain value of k, it may be difficult or impossible to explicitly determine K′, and so q cannot be explicitly determined. Conversely, it may be possible to evaluate φ(q) for a certain value of q, but it may be impossible to determine the corresponding value of k. (Recall that
, or K yields an evaluation of the other two functions. However, such evaluations may not be very explicit. For example, if K(k) is known for a certain value of k, it may be difficult or impossible to explicitly determine K′, and so q cannot be explicitly determined. Conversely, it may be possible to evaluate φ(q) for a certain value of q, but it may be impossible to determine the corresponding value of k. (Recall that 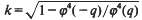 [1, p. 102].)
[1, p. 102].)
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1995
References
- 12
- Cited by


