Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T06:07:51.516Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE THETA OPERATOR FOR MODULAR FORMS MODULO PRIME POWERS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  22 January 2016

Imin Chen  and
Ian Kiming
Imin Chen
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, B.C., V5A 1S6, Canada email [email protected]
Ian Kiming
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen Ø, Denmark email [email protected]
Get access

Abstract

We consider the classical theta operator 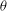${\it\theta}$ on modular forms modulo 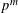$p^{m}$ and level 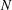$N$ prime to 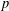$p$, where 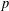$p$ is a prime greater than three. Our main result is that 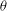${\it\theta}$ mod 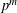$p^{m}$ will map forms of weight 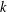$k$ to forms of weight 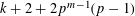$k+2+2p^{m-1}(p-1)$ and that this weight is optimal in certain cases when 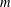$m$ is at least two. Thus, the natural expectation that 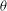${\it\theta}$ mod 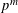$p^{m}$ should map to weight 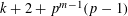$k+2+p^{m-1}(p-1)$ is shown to be false. The primary motivation for this study is that application of the 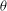${\it\theta}$ operator on eigenforms mod 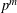$p^{m}$ corresponds to twisting the attached Galois representations with the cyclotomic character. Our construction of the 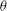${\it\theta}$-operator mod 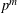$p^{m}$ gives an explicit weight bound on the twist of a modular mod 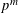$p^{m}$ Galois representation by the cyclotomic character.

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms 11F80: Galois representations
Type
Research Article
Information
Mathematika , Volume 62 , Issue 2 , 2016 , pp. 321 - 336
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chen, I., Kiming, I. and Rasmussen, J. B., On congruences mod p m between eigenforms and their attached Galois representations. J. Number Theory (3) 130 2010, 608–619.Google Scholar
Chen, I., Kiming, I. and Wiese, G., On modular Galois representations modulo prime powers. Int. J. Number Theory 9 2013, 91–113.CrossRefGoogle Scholar
Coleman, R. and Stein, W., Approximation of eigenforms of infinite slope by eigenforms of finite slope. In Geometric Aspects of Dwork Theory, Vols I, II, Walter de Gruyter (Berlin, 2004), 437–449.Google Scholar
Deligne, P. and Rapoport, M., Les schémas de modules de courbes elliptiques. In Modular Functions of One Variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972 (Lecture Notes in Mathematics 349 ) (eds Deligne, P. and Kuyk, W.), Springer (Berlin, 1973), 143–316.Google Scholar
Diamond, F. and Im, J., Modular forms and modular curves. In Seminar on Fermat’s Last Theorem (Toronto, ON, 1993–1994) (CMS Conference Proceedings 17 ), American Mathematical Society (1995), 39–133.Google Scholar
Diamond, F. and Shurman, J., A First Course in Modular Forms (Graduate Texts in Mathematics 228 ), Springer (2005), 19–24.Google Scholar
Edixhoven, B., The weight in Serre’s conjectures on modular forms. Invent. Math. (3) 109 1992, 563–594.Google Scholar
Gross, B., A tameness criterion for Galois representations associated to modular forms mod p . Duke Math. J. 61(2) 1990, 445–517.Google Scholar
Igusa, J.-I., Class number of a definite quaternion with prime discriminant. Proc. Natl. Acad. Sci. USA 44 1958, 312–314.Google Scholar
Jochnowitz, N., Congruences between systems of eigenvalues of modular forms. Trans. Amer. Math. Soc. 270 1982, 269–285.Google Scholar
Katz, N. M., p-adic properties of modular schemes and modular forms. In Modular Functions of One Variable, III (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972) (Lecture Notes in Mathematics 350 ), Springer (Berlin, 1973), 69–190.Google Scholar
Katz, N. M., A result on modular forms in characteristic p . In Modular Functions of One Variable V (Lecture Notes in Mathematics 601 ) (eds Serre, J.-P. and Zagier, D. B.), Springer (1977), 53–61.Google Scholar
Katz, N. M., On a question of Zannier, https://web.math.princeton.edu/∼nmk/zannier8.pdf.Google Scholar
Kiming, I., On the asymptotics of the number of p̄-core partitions of integers. Acta Arith. 80 1997, 127–139.Google Scholar
Queen, C., The existence of p-adic abelian L-functions. In Number Theory and Algebra, (ed. Zassenhaus, H.), Academic Press (1977), 263–288.Google Scholar
Serre, J.-P., Congruences et formes modulaires [d’après H. P. F. Swinnerton-Dyer]. In Séminaire Bourbaki (Lecture Notes in Mathematics 317 ), Springer (1973), 319–338.Google Scholar
Serre, J.-P., Formes modulaires et fonctions zêta p-adiques. In Modular Functions of One Variable III (Lecture Notes in Mathematics 350 ) (eds Kuyk, W. and Serre, J.-P.), Springer (1973), 191–268.CrossRefGoogle Scholar
Swinnerton-Dyer, H. P. F., On ℓ-adic representations and congruences for coefficients of modular forms. In Modular Functions of One Variable III (Lecture Notes in Mathematics 350 ) (eds Kuyk, W. and Serre, J.-P.), Springer (1973), 1–55.Google Scholar
Taixés i Ventosa, X. and Wiese, G., Computing congruences of modular forms and Galois representations modulo prime powers. In Arithmetic, Geometry, Cryptography and Coding Theory 2009 (Contemporary Mathematics 521 ) (eds Kohel, D. and Rolland, R.), American Mathematical Society (Providence, RI, 2010), 145–166.Google Scholar
Washington, L. C., Introduction to Cyclotomic Fields (Graduate Texts in Mathematics 83 ), Springer (1982).Google Scholar