ON SMALL BASES FOR WHICH 1 HAS COUNTABLY MANY EXPANSIONS

Abstract

Let 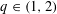$q\in (1,2)$. A 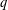$q$-expansion of a number $x$ in 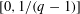$[0,1/(q-1)]$ is a sequence 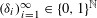$({\it\delta}_{i})_{i=1}^{\infty }\in \{0,1\}^{\mathbb{N}}$ satisfying

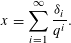$$\begin{eqnarray}x=\mathop{\sum }_{i=1}^{\infty }\frac{{\it\delta}_{i}}{q^{i}}.\end{eqnarray}$$

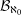Let ${\mathcal{B}}_{\aleph _{0}}$ denote the set of 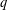$q$ for which there exists $x$ with a countable number of 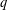$q$-expansions, and let 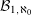${\mathcal{B}}_{1,\aleph _{0}}$ denote the set of 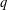$q$ for which 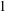$1$ has a countable number of 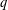$q$-expansions. In Erdős et al [On the uniqueness of the expansions 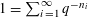$1=\sum _{i=1}^{\infty }q^{-n_{i}}$. Acta Math. Hungar.58 (1991), 333–342] it was shown that 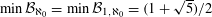$\min {\mathcal{B}}_{\aleph _{0}}=\min {\mathcal{B}}_{1,\aleph _{0}}=(1+\sqrt{5})/2$, and in S. Baker [On small bases which admit countably many expansions. J. Number Theory147 (2015), 515–532] it was shown that 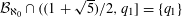${\mathcal{B}}_{\aleph _{0}}\cap ((1+\sqrt{5})/2,q_{1}]=\{q_{1}\}$, where 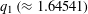$q_{1}\,({\approx}1.64541)$ is the positive root of $x^{6}-x^{4}-x^{3}-2x^{2}-x-1=0$. In this paper we show that the second smallest point of 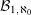${\mathcal{B}}_{1,\aleph _{0}}$ is 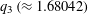$q_{3}\,({\approx}1.68042)$, the positive root of 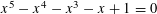$x^{5}-x^{4}-x^{3}-x+1=0$. En route to proving this result, we show that 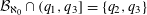${\mathcal{B}}_{\aleph _{0}}\cap (q_{1},q_{3}]=\{q_{2},q_{3}\}$, where 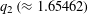$q_{2}\,({\approx}1.65462)$ is the positive root of 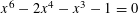$x^{6}-2x^{4}-x^{3}-1=0$.