Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T04:33:10.311Z Has data issue: false hasContentIssue false
  • English
  • Français

On Kruskal's cascades and counting containments in a set of subsets

Part of: Combinatorics

Published online by Cambridge University Press:  26 February 2010

David E. Daykin  and
Peter Frankl
David E. Daykin
Affiliation:
Dept. of Mathematics, The University of Reading, Whiteknights, Reading RG6 2AX
Peter Frankl
Affiliation:
C.N.R.S., Paris, France
Get access

Abstract

Let ℱ be a set of m subsets of X = {1,2,…, n}. We study the maximum number λ of containments Y ⊂ Z with Y, Z ∊ ℱ. Theorem 9. 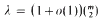, if, and only if, ml/n → 1. When n is large and members of ℱ have cardinality k or k–1 we determine λ. For this we bound (ΔN)/N where ΔN is the shadow of Kruskal's k-cascade for the integer N. Roughly, if m ∼ N + ΔN, then λ ∼ kN with infinitely many cases of equality. A by-product is Theorem 7 of LYM posets.

MSC classification

Secondary: 05A05: Permutations, words, matrices
Type
Research Article
Information
Mathematika , Volume 30 , Issue 1 , June 1983 , pp. 133 - 141
Copyright
Copyright © University College London 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Ahlswede, R. and Kalona, G. O. H.. Graphs with maximal number of adjacent pairs of edges. Acta Math. Acad. Sci. Hungar., 32 (1978), 97–120.CrossRefGoogle Scholar
2.Daykin, D. E.. A simple proof of the Kruskal Katona theorem. J. Combinatorial Theory, 17 (1974), 252–253.CrossRefGoogle Scholar
3.Daykin, D. E.. An algorithm for cascades giving Katona-type inequalities. Nanta Math., 8 (1975), 78–83.Google Scholar
4.Daykin, D. E. and Frankl, P.. Inequalities for subsets of a set and KLYM posets. SIAM J. on Algebraic and Discrete Methods, 4 (1983), 67–69.CrossRefGoogle Scholar
5.Graham, R. L. and Harper, L. H.. Some results on matching in bipartite graphs. SIAM J. Appl. Math., 17 (1969), 1017–1022.CrossRefGoogle Scholar
6.Harper, L. H.. Optimal assignments of numbers to vertices. J. Soc. Indust. Appl. Math., 12 (1964), 131–135.CrossRefGoogle Scholar
7.Harper, L. H.. Optimal numberings and isoperimetric problems on graphs. J. Combinatorial Theory, 1 (1966). 385393.CrossRefGoogle Scholar
8.Katona, G.. A theorem for finite sets. Theory of Graphs, Proc. of Colloquium, Tihany, Hungary (1966), Eds. Erdős, P. and Katona, G., 187–207.Google Scholar
9.Kleitman, D. J.. A conjecture of Erdős Katona on commensurable pairs among subsets of an n-set. Theory of Graphs, Proc. of Colloquium, Tihany, Hungary (1966), Eds. Erdős, P. and Katona, G., 215218.Google Scholar
10.Kleitman, D. J.. An extremal property of antichains in partial orders: The LYM property and some of its implications and applications. Combinatorics, Eds. Hall, M. and van Lint, J. H., Math. Centre Tracts, Vol. 55 (Math. Centre, Amsterdam, 1974) 77–90.Google Scholar
11.Kruskal, J. B.. The number of simplices in a complex. Math. Optimization Techniques, Ed. Bellman, R. (University of California Press, 1963), 251–278.CrossRefGoogle Scholar