A note on the axially symmetrical punch problem

Extract

In a recent paper Segedin [1] has derived a solution of the problem in which a perfectly rigid punch in the form of a solid of revolution of prescribed shape with axis along the z-axis bears normally on the boundary z = 0 of the semi-infinite elastic body z ≥ 0, so that the area of contact is a circle whose radius is a. Segedin solves the problem by building up the solution in a direct way which avoids both the use of dual integral equations and the introduction of an awkward system of curvilinear coordinates. By introducing a kernel function K(ξ), Segedin derives new potentials of the form

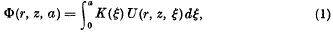
where U(r, z, a) is the solution of the simplest punch problem (namely that of a flat-ended punch) satisfying the mixed boundary conditions

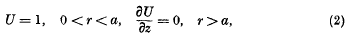
on the boundary z = 0. It can then be easily shown that, under wide conditions on K, the function Φ (r, z, a) satisfies the boundary conditions

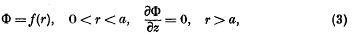
provided that K(ξ) is chosen so that