Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T05:21:41.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on difference-covers that are not k-sum-covers

Part of: Designs and configurations

Published online by Cambridge University Press:  26 February 2010

T. H. Jackson  and
F. Rehman
T. H. Jackson
Affiliation:
Department of Mathematics, University of York, York YO1 5DD.
F. Rehman
Affiliation:
Department of Mathematics, University of York, York YO1 5DD.
Get access

Extract

For some integer modulus q let F be a subset of Z(q), the additive group of residues modulo q. As in «1» we shall write

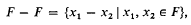
and

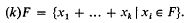
MSC classification

Secondary: 05B10: Difference sets (number-theoretic, group-theoretic, etc.)
Type
Research Article
Information
Mathematika , Volume 21 , Issue 1 , June 1974 , pp. 107 - 109
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Jackson, T. H., Williamson, J. H. and Woodall, D. R.. “Difference-covers that are not k-sum covers. I”, Proc. Camb. Phil. Soc, 72 (1972), 425–438.CrossRefGoogle ScholarPubMed
2.Jackson, T. H.. “Asymmetric sets of residues”, Mathematika, 19 (1972), 191–199.CrossRefGoogle Scholar
3.Connolly, D.. “Integer difference covers which are not k-sum covers, for k = 6, 7”, Proc. Camb. Phil. Soc, 74 (1973), 17–28.CrossRefGoogle Scholar
4.Haight, J. A.. “Difference covers which have small k-sums for any k”, Mathematika, 20 (1973), 109–118.CrossRefGoogle Scholar