Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T16:41:03.477Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIDIMENSIONAL VAN DER CORPUT SETS AND SMALL FRACTIONAL PARTS OF POLYNOMIALS

Part of: Diophantine approximation, transcendental number theory Exponential sums and character sums

Published online by Cambridge University Press:  07 January 2019

Manfred G. Madritsch  and
Robert F. Tichy
Manfred G. Madritsch
Affiliation:
Université de Lorraine, Institut Elie Cartan de Lorraine, UMR 7502, Vandoeuvre-lès-Nancy, F-54506, France CNRS, Institut Elie Cartan de Lorraine, UMR 7502, Vandoeuvre-lès-Nancy, F-54506, France email [email protected]
Robert F. Tichy
Affiliation:
Department for Analysis and Number Theory, Graz University of Technology, A-8010 Graz, Austria email [email protected]
Get access

Abstract

We establish Diophantine inequalities for the fractional parts of generalized polynomials, in particular for sequences 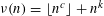$\unicode[STIX]{x1D708}(n)=\lfloor n^{c}\rfloor +n^{k}$ with 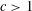$c>1$ a non-integral real number and 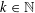$k\in \mathbb{N}$, as well as for 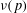$\unicode[STIX]{x1D708}(p)$ where 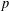$p$ runs through all prime numbers. This is related to classical work of Heilbronn and to recent results of Bergelson et al.

MSC classification

Primary: 11J54: Small fractional parts of polynomials and generalizations
Secondary: 11L15: Weyl sums 11L20: Sums over primes
Type
Research Article
Information
Mathematika , Volume 65 , Issue 2 , 2019 , pp. 400 - 435
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, R. C., Diophantine Inequalities (London Mathematical Society Monographs New Series 1 ), The Clarendon Press–Oxford University Press (New York, 1986); MR 865981.Google Scholar
Baker, R., Small fractional parts of polynomials. Funct. Approx. Comment. Math. 55(1) 2016, 131–137; MR 3549017.Google Scholar
Baker, R., Fractional parts of polynomials over the primes. Mathematika 63(3) 2017, 715–733; MR 3731301.Google Scholar
Baker, R. C. and Kolesnik, G., On the distribution of p 𝛼 modulo one. J. reine angew. Math. 356 1985, 174–193; MR 779381 (86m:11053).Google Scholar
Bergelson, V., Kolesnik, G., Madritsch, M., Son, Y. and Tichy, R., Uniform distribution of prime powers and sets of recurrence and van der Corput sets in k . Israel J. Math. 201(2) 2014, 729–760; MR 3265301.Google Scholar
Bergelson, V., Kolesnik, G. and Son, Y., Uniform distribution of subpolynomial functions along primes and applications. Preprint, 2015, arXiv:1503.04960.Google Scholar
Bergelson, V., Leibman, A. and Lesigne, E., Intersective polynomials and the polynomial Szemerédi theorem. Adv. Math. 219(1) 2008, 369–388; MR 2435427.Google Scholar
Bergelson, V. and Lesigne, E., Van der Corput sets in d . Colloq. Math. 110(1) 2008, 1–49; MR 2353898 (2008j:11089).Google Scholar
Bergelson, V. and Moreira, J., Van der Corput’s difference theorem: some modern developments. Indag. Math. (N.S.) 27(2) 2016, 437–479; MR 3479166.Google Scholar
Boshernitzan, M., Kolesnik, G., Quas, A. and Wierdl, M., Ergodic averaging sequences. J. Anal. Math. 95 2005, 63–103; MR 2145587 (2006b:37011).Google Scholar
Bourgain, J., Ruzsa’s problem on sets of recurrence. Israel J. Math. 59(2) 1987, 150–166; MR 920079 (89d:11012).Google Scholar
Bourgain, J., Demeter, C. and Guth, L., Proof of the main conjecture in Vinogradov’s mean value theorem for degrees higher than three. Ann. of Math. (2) 184(2) 2016, 633–682; MR 3548534.Google Scholar
Cook, R. J., On the fractional parts of a set of points. Mathematika 19 1972, 63–68; MR 0330060.Google Scholar
Cook, R. J., On the fractional parts of a set of points. II. Pacific J. Math. 45 1973, 81–85; MR 0330064.Google Scholar
Cook, R. J., Diophantine inequalities with mixed powers (mod  1). Proc. Amer. Math. Soc. 57(1) 1976, 29–34; MR 0401647 (53 #5474).Google Scholar
Danicic, I., On the fractional parts of 𝜃x 2 and 𝜙x 2 . J. Lond. Math. Soc. (2) 34 1959, 353–357; MR 0166160.Google Scholar
Davenport, H., On a theorem of Heilbronn. Q. J. Math. Oxford Ser. (2) 18 1967, 339–344; MR 0223307 (36 #6355).Google Scholar
Drmota, M. and Tichy, R. F., Sequences, Discrepancies and Applications (Lecture Notes in Mathematics 1651 ), Springer (Berlin, 1997); MR 1470456 (98j:11057).Google Scholar
Furstenberg, H., Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 1977, 204–256; MR 0498471 (58 #16583).Google Scholar
Grabner, P. J., Harmonische analyse, Gleichverteilung und Ziffernentwicklungen. PhD Thesis, Vienna University of Technology (TU Wien), 1989.Google Scholar
Graham, S. W. and Kolesnik, G., Van der Corput’s Method of Exponential Sums (London Mathematical Society Lecture Note Series 126 ), Cambridge University Press (Cambridge, 1991); MR 1145488 (92k:11082).Google Scholar
Hardy, G. H. and Littlewood, J. E., Some problems of diophantine approximation Part I. The fractional part of n k 𝜃. Acta Math. 37(1) 1914, 155–191; MR 1555098.Google Scholar
Harman, G., Trigonometric sums over primes. I. Mathematika 28(2) 1981, 249–254 (1982);MR 645105 (83j:10045).Google Scholar
Heilbronn, H., On the distribution of the sequence n 2𝜃(mod 1). Q. J. Math. Oxford Ser. 19 1948, 249–256; MR 0027294 (10,284c).Google Scholar
Kamae, T. and Mendès France, M., Van der Corput’s difference theorem. Israel J. Math. 31(3–4) 1978, 335–342; MR 516154 (80a:10070).Google Scholar
Kirschenhofer, P. and Tichy, R. F., On uniform distribution of double sequences. Manuscripta Math. 35(1–2) 1981, 195–207; MR 627933.Google Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences (Pure and Applied Mathematics), Wiley-Interscience [John Wiley] (New York, 1974); MR 0419394 (54 #7415).Google Scholar
Lê, T. H., Problems and results on intersective sets. In Combinatorial and Additive Number Theory—CANT 2011 and 2012 (Springer Proceedings in Mathematics & Statistics 101 ), Springer (New York, 2014), 115–128; MR 3297075.Google Scholar
Lê, T. H. and Spencer, C. V., Intersective polynomials and Diophantine approximation. Int. Math. Res. Not. IMRN 2014(5) 2014, 1153–1173; MR 3178593.Google Scholar
Lê, T. H. and Spencer, C. V., Intersective polynomials and Diophantine approximation, II. Monatsh. Math. 177(1) 2015, 79–99; MR 3336334.Google Scholar
Liu, M.-C., On the fractional parts of 𝜃n k and 𝜙n k . Q. J. Math. Oxford Ser. (2) 21 1970, 481–486; MR 0279046.Google Scholar
Losert, V. and Tichy, R. F., On uniform distribution of subsequences. Probab. Theory Related Fields 72(4) 1986, 517–528; MR 847384.Google Scholar
Madritsch, M. G. and Tichy, R. F., Dynamical systems and uniform distribution of sequences. In From Arithmetic to Zeta-functions, Springer (Cham, 2016), 263–276; MR 3642360.Google Scholar
Matomäki, K., The distribution of 𝛼p modulo one. Math. Proc. Cambridge Philos. Soc. 147(2) 2009, 267–283; MR 2525926.Google Scholar
Mauduit, C. and Rivat, J., Répartition des fonctions q-multiplicatives dans la suite ([n c ]) n N , c > 1. Acta Arith. 71(2) 1995, 171–179; MR 1339124 (96g:11116).+1.+Acta+Arith.+71(2)+1995,+171–179;+MR+1339124+(96g:11116).>Google Scholar
Mauduit, C. and Rivat, J., Propriétés q-multiplicatives de la suite n c , c > 1. Acta Arith. 118(2) 2005, 187–203; MR 2141049 (2006e:11151).+1.+Acta+Arith.+118(2)+2005,+187–203;+MR+2141049+(2006e:11151).>Google Scholar
Mauduit, C. and Rivat, J., Sur un problème de Gelfond: la somme des chiffres des nombres premiers. Ann. of Math. (2) 171(3) 2010, 1591–1646; MR 2680394 (2011j:11137).Google Scholar
Montgomery, H. L., Ten Lectures on the Interface Between Analytic Number Theory and Harmonic Analysis (CBMS Regional Conference Series in Mathematics 84 ), Conference Board of the Mathematical Sciences (Washington, DC, 1994); MR 1297543 (96i:11002).Google Scholar
Morgenbesser, J. F., The sum of digits of n c . Acta Arith. 148(4) 2011, 367–393; MR 2800701 (2012f:11195).Google Scholar
Müllner, C. and Spiegelhofer, L., Normality of the Thue–Morse sequence along Piatetski–Shapiro sequences, II. Israel J. Math. 220(2) 2017, 691–738; MR 3666442.Google Scholar
Nair, R., On certain solutions of the Diophantine equation x - y = p (z). Acta Arith. 62(1) 1992, 61–71; MR 1179010 (94a:11124).Google Scholar
Nair, R., On uniformly distributed sequences of integers and Poincaré recurrence. Indag. Math. (N.S.) 9(1) 1998, 55–63; MR 1618231.Google Scholar
Nair, R., On uniformly distributed sequences of integers and Poincaré recurrence. II. Indag. Math. (N.S.) 9(3) 1998, 405–415; MR 1692161.Google Scholar
Nathanson, M. B., Additive Number Theory: The Classical Bases (Graduate Texts in Mathematics 164 ), Springer (New York, 1996); MR 1395371 (97e:11004).Google Scholar
Rice, A., Sárközy’s theorem for O-intersective polynomials. Acta Arith. 157(1) 2013, 69–89; MR 3005099.Google Scholar
Ruzsa, I. Z., Connections between the uniform distribution of a sequence and its differences. In Topics in Classical Number Theory, Vols. I, II (Budapest, 1981) (Colloquia Mathematica Societatis János Bolyai 34 ), North-Holland (Amsterdam, 1984), 1419–1443; MR 781190 (86e:11062).Google Scholar
Sárközy, A., On difference sets of sequences of integers. I. Acta Math. Acad. Sci. Hungar. 31(1–2) 1978, 125–149; MR 0466059 (57 #5942).Google Scholar
Schmidt, W. M., Small Fractional Parts of Polynomials (Regional Conference Series in Mathematics, 32 ), American Mathematical Society (Providence, RI, 1977); MR 0457360.Google Scholar
Slijepčević, S., On van der Corput property of squares. Glas. Mat. Ser. III 45(65)(2) 2010, 357–372; MR 2753306 (2012c:11017).Google Scholar
Slijepčević, S., On van der Corput property of shifted primes. Funct. Approx. Comment. Math. 48(1) 2013, 37–50; MR 3086959.Google Scholar
Spiegelhofer, L., Piatetski–Shapiro sequences via Beatty sequences. Acta Arith. 166(3) 2014, 201–229; MR 3283620.Google Scholar
Tichy, R. and Zeiner, M., Baire results of multisequences. Unif. Distrib. Theory 5(1) 2010, 13–44; MR 2804660.Google Scholar
Vaaler, J. D., Some extremal functions in Fourier analysis. Bull. Amer. Math. Soc. (N.S.) 12(2) 1985, 183–216; MR 776471 (86g:42005).Google Scholar
Vinogradov, I. M., Analytischer Beweis des Satzes über die Verteilung der Bruchteile eines ganzen Polynoms. Bull. Acad. Sci. USSR 21(6) 1927, 567–578 (in Russian).Google Scholar
Weyl, H., Über die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 77 1916, 313–352 (in German).Google Scholar
Wierdl, M., Almost everywhere convergence and recurrence along subsequences in ergodic theory. PhD Thesis, The Ohio State University, ProQuest LLC, Ann Arbor, MI, 1989; MR 2638457.Google Scholar
Wooley, T. D., New estimates for smooth Weyl sums. J. Lond. Math. Soc. (2) 51(1) 1995, 1–13; MR 1310717.Google Scholar
Wooley, T. D., The cubic case of the main conjecture in Vinogradov’s mean value theorem. Adv. Math. 294 2016, 532–561; MR 3479572.Google Scholar
Zaharescu, A., Small values of n 2𝛼 (mod 1). Invent. Math. 121(2) 1995, 379–388; MR 1346212 (96d:11079).Google Scholar