Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T01:20:13.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Metric Diophantine approximation with two restricted variables II: A prime and a square-free integer

Published online by Cambridge University Press:  26 February 2010

Glyn Harman
Glyn Harman
Affiliation:
Department of Pure Mathematics, University College, P.O. Box 78, Cardiff CF1 1XL.
Get access

Extract

In this paper we continue the investigation begun in [6] concerning the number of solutions of the inequality

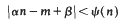
for almost all α (in the sense of Lebesgue measure on ℝ), where β is a given real number, 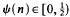, and both m and n are confined to sets of numbertheoretic interest. Our aim is to extend existing results ([7], [8], [5] for example), where only n is restricted. Here we shall prove the following result where, as elsewhere in this paper, p denotes a prime, and a square-free integer may be positive or negative.

Type
Research Article
Information
Mathematika , Volume 35 , Issue 1 , June 1988 , pp. 59 - 68
Copyright
Copyright © University College London 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Davenport, H.. Multiplicative Number Theory, 2nd ed. revised by H. L. Montgomery (Springer, New York, 1980).Google Scholar
2.Gá, I. S. and Koksma, J. F.. Sur l'ordre de grandeur des fonctions sommables. ltulag. Math., 12 (1950), 192–207.Google Scholar
3.Halberstam, H. and Richert, H.-E.. Sieve Methods(Academic Press, London, 1974).Google Scholar
4.Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers 5th ed. (University Press, 1979).Google Scholar
5.Harman, G.. Some theorems in the metric theory of Diophantine approximation. Math. Proc Camb. Phil. Soc., 99 (1986), 385–394.CrossRefGoogle Scholar
6.Harman, G.. Metric Diophantine approximation with two restricted variables I: two square-free integers, or integers in arithmetic progressions. Preprint, Cardiff 1986.Google Scholar
7.Le Veque, W. J.. On the frequency of small fractional parts in certain real sequences III. J. Reine Angew. Math., 202 (1959), 215–220.CrossRefGoogle Scholar
8.Schmidt, W. M.. Metrical theorems on fractional parts of sequences. Trans. Amer. Math. Soc., 110 (1964), 493–518.Google Scholar
9.Sprindzuk, V. G.. Metric Theory of Diophantine Approximation, Silverman, R. A. (Winston/Wiley, New York, 1980).Google Scholar