Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T11:52:25.445Z Has data issue: false hasContentIssue false
  • English
  • Français

A lower bound for the L1-norm of certain exponential sums

Published online by Cambridge University Press:  26 February 2010

P. G. Dixon
P. G. Dixon
Affiliation:
Department of Pure Mathematics, Sheffield.
Get access

Extract

Littlewood [5, Problem 4.19, originally 4] conjectured that there is an absolute constant C > 0 such that, for every sequence of distinct integers n1, n2, n3, …, if

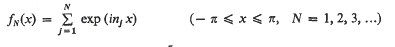
then

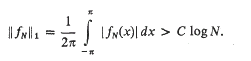
Cohen [2] showed

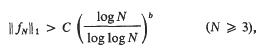
for some absolute constant C, with b = 1/8. Davenport [3] gave a more explicit version of Cohen's proof and improved the estimate to b = 1/4. Pichorides [6] added another refinement to obtain b = ½, and has, more recently, obtained ‖fN‖1>C(log N)1/2. This seems to be the best estimate so far without restriction on the sequences. We shall show that the methods of Davenport and Pichorides may be extended to obtain better results for certain classes of sequences. Specifically, we prove the following theorems.

Type
Research Article
Information
Mathematika , Volume 24 , Issue 2 , December 1977 , pp. 182 - 188
Copyright
Copyright © University College London 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Chidambaraswamy, J.. “On a conjecture of J. E. Littlewood”, J. Reine Angew. Math., 272 (1975), 25–31.Google Scholar
2.Cohen, P. J.. “On a conjecture of Littlewood and idempotent measures”, Amer. J. Math., 82 (1960), 191–212.CrossRefGoogle Scholar
3.Davenport, H.. “On a theorem of P. J. Cohen”, Mathematika, 7 (1960), 93–97.CrossRefGoogle Scholar
4.Hardy, G. H. and Littlewood, J. E.. “A new proof of a theorem of rearrangements”, J. London Math. Soc. (1), 23 (1948), 163–168.CrossRefGoogle Scholar
5.Hayman, W. K.. Research problems in function theory, (University of London, 1967).Google Scholar
6.Pichorides, S. K.. “A lower bound for the L1 norm of exponential sums”, Mathematika, 21 (1974), 155–159.CrossRefGoogle Scholar
7.Zygmund, A.. Trigonometric series, Vol. I (Cambridge University Press, 1959).Google Scholar