Article contents
Isoperimetric problems for tilings, corrigendum
Published online by Cambridge University Press: 26 February 2010
Extract
In [1] I made the following conjecture. If we tile a convex polygon of at most six sides with N convex tiles of areas a1, …,aN, then the total perimeter of the tiles is never less than the total perimeter of N regular hexagons of areas a1, …, aN. In order to show that the condition of the convexity of the tiles cannot be omitted I constructed a tiling with an equal number of “pentagons” and “heptagons” of perimeters and areas 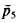 and
and 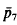 , and ā5 and ā7, respectively. In a letter to me R. Schneider kindly pointed out that, in contrast to the value given in [1], the value of the quotient
, and ā5 and ā7, respectively. In a letter to me R. Schneider kindly pointed out that, in contrast to the value given in [1], the value of the quotient 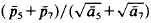 was equal to 3.7263… This being greater than √8√3 = 3–7224… the tiling given in [1] does not yield the desired counter-example. In what follows we shall construct a tiling for which the respective quotient will turn out to be less than √8√3.
was equal to 3.7263… This being greater than √8√3 = 3–7224… the tiling given in [1] does not yield the desired counter-example. In what follows we shall construct a tiling for which the respective quotient will turn out to be less than √8√3.
- Type
- Correction
- Information
- Copyright
- Copyright © University College London 1986
References
- 1
- Cited by


