Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Elsholtz, Christian
2006.
Additive decomposability of multiplicatively defined sets.
Functiones et Approximatio Commentarii Mathematici,
Vol. 35,
Issue. none,
Elsholtz, Christian
2009.
Combinatorial Number Theory and Additive Group Theory.
p.
213.
Gyarmati, Katalin
Konyagin, Sergei
and
Sárközy, András
2013.
On the reducibility of large sets of residues modulo p.
Journal of Number Theory,
Vol. 133,
Issue. 7,
p.
2374.
Dartyge, Cécile
and
Sárközy, András
2013.
On additive decompositions of the set of primitive roots modulo p.
Monatshefte für Mathematik,
Vol. 169,
Issue. 3-4,
p.
317.
Elsholtz, Christian
and
Harper, Adam
2014.
Additive decompositions of sets with restricted prime factors.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 10,
p.
7403.
Green, Ben
and
Harper, Adam J
2014.
Inverse questions for the large sieve.
Geometric and Functional Analysis,
Vol. 24,
Issue. 4,
p.
1167.
Elsholtz, Christian
and
Wurzinger, Lena
2024.
Sumsets in the set of squares.
The Quarterly Journal of Mathematics,
Vol. 75,
Issue. 4,
p.
1243.


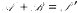 where, ℝ′ differs from the set of primes in finitely many elements only and
where, ℝ′ differs from the set of primes in finitely many elements only and 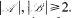 .
.