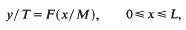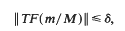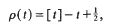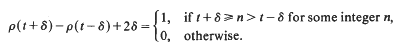Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huxley, M. N.
1992.
Séminaire de Théorie des Nombres, Paris, 1989–90.
Vol. 102,
Issue. ,
p.
93.
Huxley, M. N.
and
Trifonov, O.
1996.
The square-full numbers in an interval.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 119,
Issue. 2,
p.
201.
Huxley, M. N.
2000.
Number Theory.
p.
157.
Huxley, M. N.
2000.
Number Theory.
p.
157.
Huxley, Martin
and
Sargos, Patrick
2006.
Points entires au voisinage d'une courbe plane de classe {$C^n$}, II.
Functiones et Approximatio Commentarii Mathematici,
Vol. 35,
Issue. none,
Howard, Ralph
and
Trifonov, Ognian
2023.
Bounding the number of lattice points near a convex curve by curvature.
Functiones et Approximatio Commentarii Mathematici,
Vol. 69,
Issue. 2,
Huxley, Martin N.
2023.
Number Theory in Memory of Eduard Wirsing.
p.
185.