Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T11:51:52.035Z Has data issue: false hasContentIssue false
  • English
  • Français

Incomplete Gauss sums

Published online by Cambridge University Press:  26 February 2010

D. H. Lehmer
D. H. Lehmer
Affiliation:
Department of Mathematics, The University of California, Berkeley, California, U.S.A.
Get access

Abstract

Let N be a positive integer. We are concerned with the sum

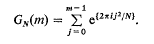
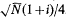Thus GN(N) is the ordinary Gauss sum. Previous methods of estimating such exponential sums have not brought to light the peculiar behaviour of GN(m) for m < N/2, namely that, for almost all values of m, GN(m) is in the vicinity of the point . A sharp estimate is given for max |GN(m)|, depending on the residue of N modulo 4. The results were suggested by graphs of GN(m) made for N near 1000. The analysis employs the Fresnel integrals and the Cornu spiral whose curvature is proportional to its arc length.

Type
Research Article
Information
Mathematika , Volume 23 , Issue 2 , December 1976 , pp. 125 - 135
Copyright
Copyright © University College London 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Hua, , Keng, Loo. “On exponential sums”, Sci. Record (new series), 1 (1957), 1–4 (Math. Revs. 20, 22).Google Scholar
2. An authoritative account of the Euler-Maclaurin summation formula will be found in Ostrowski, A. M., “On the remainder term of the Euler-Maclaurin formula”, Jn. Math, reine angew, 239-240 (1969), 268–286CrossRefGoogle Scholar
3.Tables of Fresnel Integrals (Akad. Nauk. SSSR. Moscow 1953).Google Scholar