Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T12:23:34.563Z Has data issue: false hasContentIssue false
  • English
  • Français

The homological grade of a module

Published online by Cambridge University Press:  26 February 2010

David Kirby  and
Hefzi A. Mehran
David Kirby
Affiliation:
Faculty of Mathematical Studies, The University, Southampton, SO9 5NH.
Hefzi A. Mehran
Affiliation:
Department of Mathematics, Kuwait University, Kuwait.
Get access

Extract

For an ideal A of a commutative ring R with identity and a unitary R-module E the notion of an E-sequence of length d in A can be extended as follows. For d = 0 the E-sequence is empty, and for d = 1 it is a subset {ai|i ∈ I} = α ⊆ A such that 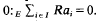. For d > 1 we may define, inductively, an E-sequence of length d in A as a sequence

of subsets of A such that a, is an E-sequence of length 1 in A and α2,…, αd is a 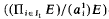-sequence of length d − 1 in A. Thus in the standard notion of E-sequence the sets αj, are singletons, and, in effect, the extended notion due to Hochster [1] and Northcott [3] the sets a; are finite. Many of the standard results concerning E-sequences when E is Noetherian extend to the above generalization when the Noetherian condition is dropped. For example it follows from the results of the present note that every maximal E-sequence has the same length (which may be infinite) and every E-sequence can be extended to a maximal E-sequence. This maximal length is inf 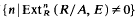which we call the homological grade of E in A and denote by hgrR (A; E). So 0 ≤ hgrR (A; E) ≤ ∞, hgrR (A; E) = 0, if, and only if, 0:EA≠0 and hgrg (A; E) = ∞, if, and only if, 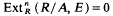for all nєℤ.

Type
Research Article
Information
Mathematika , Volume 35 , Issue 1 , June 1988 , pp. 114 - 125
Copyright
Copyright © University College London 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Hochster, M.. Grade sensitive modules and perfect modules. Proc. London Math. Soc. (3), 29 (1974), 55–76.CrossRefGoogle Scholar
2.Northcott, D. G.. Lessons on rings, modules and multiplicities (Camb. Univ. Press, 1968).CrossRefGoogle Scholar
3.Northcott, D. G.. Finite free resolutions, Cambridge Tract No. 71 (Camb. Univ. Press, 1976).CrossRefGoogle Scholar
4.Peskine, C. and Szpiro, L.. Dimension projective finie et cohomologie locale. Publ. Math. Inst. des Haute Études Sci. Paris, 42 (1973), 47–119.CrossRefGoogle Scholar
5.Walker, R. J.. Algebraic Curves, Princeton Mathematical Series No. 13 (Princeton Univ. Press, 1950).Google Scholar