Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T05:10:30.757Z Has data issue: false hasContentIssue false
  • English
  • Français

FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES

Part of: Diophantine approximation, transcendental number theory Multiplicative number theory Exponential sums and character sums

Published online by Cambridge University Press:  29 November 2017

Roger Baker
Roger Baker*
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602, U.S.A. email [email protected]
Get access

Abstract

Let 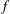$f$ be a polynomial of degree 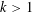$k>1$ with irrational leading coefficient. We obtain results of the form

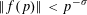$$\begin{eqnarray}\Vert f(p)\Vert <p^{-\unicode[STIX]{x1D70E}}\end{eqnarray}$$
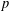for infinitely many primes $p$ that supersede those of Harman [Trigonometric sums over primes I. Mathematika28 (1981), 249–254; Trigonometric sums over primes II. Glasg. Math. J.24 (1983), 23–37] and Wong [On the distribution of 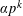$\unicode[STIX]{x1D6FC}p^{k}$ modulo 1. Glasg. Math. J.39 (1997), 121–130].

MSC classification

Primary: 11J54: Small fractional parts of polynomials and generalizations
Secondary: 11L20: Sums over primes 11N36: Applications of sieve methods
Type
Research Article
Information
Mathematika , Volume 63 , Issue 3 , 2017 , pp. 715 - 733
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, R. C., Diophantine Inequalities (London Mathematical Society Monographs New Series 1 ), Oxford University Press (Oxford, 1986).Google Scholar
Baker, R. C., Correction to “Weyl sums and Diophantine approximation [J. Lond. Math. Soc. (2) 25 (1982), 25–34]”. J. Lond. Math. Soc. (2) 46 1992, 202–204.Google Scholar
Baker, R. C., Small fractional parts of polynomials. Funct. Approx. Comment. Math. 55 2016, 131–137.CrossRefGoogle Scholar
Baker, R. C. and Harman, G., On the distribution of 𝛼p k modulo one. Mathematika 48 1991, 170–184.CrossRefGoogle Scholar
Baker, R. C. and Weingartner, A., A ternary Diophantine inequality over primes. Acta Arith. 162 2014, 159–196.Google Scholar
Bourgain, J., Demeter, C. and Guth, L., Proof of the main conjecture in Vinogradov’s mean value theorem for degrees higher than three. Ann. of Math. (2) 184 2016, 633–682.Google Scholar
de Bruijn, N. G., On the number of positive integers ⩽x and free of prime factors > y. II. Nederl. Akad. Wetensch. Proc. Ser. A 69 1966, 239–247.Google Scholar
Cochrane, T., Exponential sums modulo prime powers. Acta Arith. 101 2002, 131–149.CrossRefGoogle Scholar
Harman, G., Trigonometric sums over primes I. Mathematika 28 1981, 249–254.Google Scholar
Harman, G., Trigonometric sums over primes II. Glasg. Math. J. 24 1983, 23–37.Google Scholar
Harman, G., On the distribution of 𝛼p modulo one. II. Proc. Lond. Math. Soc. (3) 72 1996, 241–260.Google Scholar
Harman, G., Prime-detecting Sieves, Princeton University Press (Princeton, NJ, 2007).Google Scholar
Hooley, C., On an elementary inequality in the theory of Diophantine approximation. In Analytic Number Theory (Allerton Park, IL, 1995), Vol. 2 (Progress in Mathematics 139 ), Birkhäuser (Boston, MA, 1996), 471–486.Google Scholar
Matomaki, K., The distribution of 𝛼p modulo one. Math. Proc. Cambridge Philos. Soc. 147 2009, 267–283.Google Scholar
Vaughan, R. C., The Hardy–Littlewood Method (Cambridge Tracts in Mathematics 125 ), 2nd edn., Cambridge University Press (Cambridge, 1997).Google Scholar
Wong, K. C., On the distribution of 𝛼p k modulo 1. Glasg. Math. J. 39 1997, 121–130.Google Scholar