Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T05:22:01.319Z Has data issue: false hasContentIssue false
  • English
  • Français

The form of the spectral functions associated with Dirac equations

Part of: Ordinary differential operators

Published online by Cambridge University Press:  26 February 2010

S. M. Riehl
S. M. Riehl
Affiliation:
Department of Mathematics, University of Northern Iowa, Cedar Falls, IA 50614-0506, U.S.A., E-mail: [email protected]
Get access

Extract

§1. Introduction. In this paper, we consider the spectral functions ρα(μ) for μ ∈ R associated with a Dirac equation on [0, ∞) given by

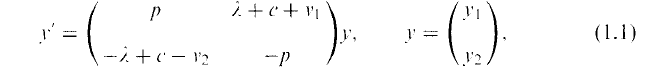
together with the initial condition

MSC classification

Secondary: 34L40: Particular operators (Dirac, one-dimensional Schrödinger, etc.)
Type
Research Article
Information
Mathematika , Volume 50 , Issue 1-2 , December 2003 , pp. 153 - 165
Copyright
Copyright © University College London 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Coddington, E. A. and Levinson, N.. Theory of Ordinary Differential Equations, McGraw Hill, (New York. 1955).Google Scholar
2.Eastham, M.S. P.. A connection formula for Sturm-Liouville spectral functions. Proc. Royal Soc. Edinburgh 130A (2000), 789–791.CrossRefGoogle Scholar
3.Eastham, M. S. P.. On the location of spectral concentration for perturbed discrete spectra, Matlwmatika, 46 (1999), 145–154.Google Scholar
4.Gilbert, D. J. and Harris, B. J.. Connection formula for spectral functions associated with singular Sturm–Liouville equations, Proc. Royal Soc. Edinburgh 130A (2000). 25–34.CrossRefGoogle Scholar
5.Gilbert, D. J. and Harris, B. J.. Bounds for the points of spectral concentration of Sturm Liouville equations, Mathematika, 47 (2000), 327–337.CrossRefGoogle Scholar
6.Gilbert, D. J., Harris, B. J. and Riehl, S. M.. The spectral function for Sturm-Liouville problems where the potential is of Wigner–von Neumann type or slowly decaying. J. Diff. Eq. 201 (2004). 139–159.CrossRefGoogle Scholar
7.Greiner, W.. Quantum Mechanics, an Introduction, Springer–Verlag (Berlin. 1994).Google Scholar
8.Harris, B. J.. The form of the spectral functions associated with Sturm–Liouvillc problems with continuous spectrum, Mathematika, 44 (1997), 149–161.CrossRefGoogle Scholar
9.Hille, E.. Lectures on Ordinary Differential Equations, Addiso–Wesley Publishing Company (Reading, Mass., 1969)Google Scholar
10.Hinton, D. B.. Klaus, M. and Shaw, J. K.. Asymptotic phase, asymptotic modulus, and Titchmarsh–Weyl coefficient for a Dirac system, J. Math. Analysis Appl. 142 (1989), 108–129.CrossRefGoogle Scholar
11.Hinton, D. B., Klaus, M. and Shaw, J. K.. Series representation and asymptotics for Titchmarsh–Weyl m-functions, Differential Integral Equations 2 (1989). no. 4, 419429.CrossRefGoogle Scholar
12.Hinton, D. B. and Shaw, J. K.. Absolutely continuous spectra of Dirac systems with long range, short range and oscillating potentials, Quart. J. Math, (2), 36 (1985), 183–213.CrossRefGoogle Scholar
13.Levitan, B. M. and Sargsjan, I. S.. Introduction to Spectral Theory, Translations of Mathematical Monographs 39. American Mathematical Society (Providence, RI, 1975).Google Scholar
14.Reed, M. and Simon, B.. Methods of Modern Mathematical Physics, III: Scattering Theory, Academic Press (New York, 1979).Google Scholar
15.Riehl, S. M.. Spectral Functions Associated with Sturm–Liouville and Dirac Equations. PhD dissertation, Northern Illinois University (2001).Google Scholar
16.Riehl, S. M.. Consequences of the connection formulae for Sturm Liouville spectral functions. Proc. Royal Soc. Edinburgh 132A (2002), 387–393.CrossRefGoogle Scholar
17.Riehl, S. M.. Connection formulae for spectral functions associated with Dirac equations. Proc. Roy. Soc. Edinburgh 134A (2004), 215–223.CrossRefGoogle Scholar
18.Whittaker, E. T. and Watson, G. N.. A Course of Modern Analysis (4th edition), Cambridge University Press (Cambridge, 1927)Google Scholar