Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barany, I.
Vempala, S.
and
Vetta, A.
2005.
Nash Equilibria in Random Games.
p.
123.
Vu, Van
2006.
Central limit theorems for random polytopes in a smooth convex set.
Advances in Mathematics,
Vol. 207,
Issue. 1,
p.
221.
Bárány, Imre
and
Vu, Van
2007.
Central limit theorems for Gaussian polytopes.
The Annals of Probability,
Vol. 35,
Issue. 4,
Bronstein, E. M.
2008.
Approximation of convex sets by polytopes.
Journal of Mathematical Sciences,
Vol. 153,
Issue. 6,
p.
727.
Bárány, I.
Fodor, F.
and
Vígh, V.
2010.
Intrinsic volumes of inscribed random polytopes in smooth convex bodies.
Advances in Applied Probability,
Vol. 42,
Issue. 3,
p.
605.
Bárány, I.
Fodor, F.
and
Vígh, V.
2010.
Intrinsic volumes of inscribed random polytopes in smooth convex bodies.
Advances in Applied Probability,
Vol. 42,
Issue. 3,
p.
605.
Bárány, Imre
and
Reitzner, Matthias
2010.
Poisson polytopes.
The Annals of Probability,
Vol. 38,
Issue. 4,
Bárány, Imre
and
Reitzner, Matthias
2010.
On the variance of random polytopes.
Advances in Mathematics,
Vol. 225,
Issue. 4,
p.
1986.
Thäle, Christoph
Turchi, Nicola
and
Wespi, Florian
2018.
Random polytopes: Central limit theorems for intrinsic volumes.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 7,
p.
3063.
Bárány, Imre
Fradelizi, Matthieu
Goaoc, Xavier
Hubard, Alfredo
and
Rote, Günter
2020.
Random polytopes and the wet part for arbitrary probability distributions.
Annales Henri Lebesgue,
Vol. 3,
Issue. ,
p.
701.
Grygierek, Jens
2021.
Multivariate Normal Approximation for Functionals of Random Polytopes.
Journal of Theoretical Probability,
Vol. 34,
Issue. 2,
p.
897.
Kwan, Matthew
Sauermann, Lisa
and
Zhao, Yufei
2022.
Extension complexity of low-dimensional polytopes.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 6,
p.
4209.
Gusakova, Anna
Reitzner, Matthias
and
Thäle, Christoph
2023.
Variance expansion and Berry-Esseen bound for the number of vertices of a random polygon in a polygon.
Annales Henri Lebesgue,
Vol. 6,
Issue. ,
p.
875.
Fodor, Ferenc
and
Papvári, Dániel I.
2024.
A Central Limit Theorem for Random Disc-Polygons in Smooth Convex Discs.
Discrete & Computational Geometry,


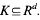 It is shown here that, with high probability,
It is shown here that, with high probability, 