Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T12:00:03.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients

Part of: Sequences and sets

Published online by Cambridge University Press:  26 February 2010

Andrew Granville  and
Olivier Ramaré
Andrew Granville
Affiliation:
Department of Mathematics, University of Georgia, Athens, Georgia 30602, U.S.A. e-mail [email protected]
Olivier Ramaré
Affiliation:
Université Nancy I, 54506 Vandoeuvre-les-Nancy, France. e-mail [email protected]
Get access

Extract

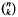The distribution of squarefree binomial coefficients. For many years, Paul Erdős has asked intriguing questions concerning the prime divisors of binomial coefficients, and the powers to which they appear. It is evident that, if k is not too small, then must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently 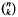is squarefree. One well-known conjecture, due to Erdős, is that 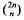is not squarefree once n > 4. Sarközy [Sz] proved this for sufficiently large n but here we return to and solve the original question.

MSC classification

Secondary: 11B65: Binomial coefficients; factorials; $q$-identities
Type
Research Article
Information
Mathematika , Volume 43 , Issue 1 , June 1996 , pp. 73 - 107
Copyright
Copyright © University College London 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BLS.Brillhart, J., Lehmer, D. H. and Selfridge, J. L.. New primality criteria and factorizations of 2m ± 1. Math. Comp., 29 (1975), 620–647.Google Scholar
Bo.Bombieri, E.. Le grand crible dans la théorie analytique des nombres. Astérisque, 18 (1987/1974), 103 pp.Google Scholar
C.Cutter, P.. Finding big prime k-tuplets. To appear.Google Scholar
Da.Davenport, H.. Multiplicative Number Theory, 2nd ed. (Springer-Verlag, New York, 1980).CrossRefGoogle Scholar
DIT.Dress, F., Iwaniec, H. and Tenenbaum, G.. Sur une somme liée   la fonction de Möbius, J. reine angew. Math., 340 (1983), 53–58.Google Scholar
EG.Erőds, P. and Graham, R. L.. Old and new problems and results in combinatorial number theory. Enseign. Math. Geneva (1980).Google Scholar
ELS.Erdős, P., Lacampagne, C. B. and Selfridge, J. L.. Estimates of the least prime factor of a binomial coefficient. Math. Comp., 61 (1993), 215–224.CrossRefGoogle Scholar
FL.Friedlander, J. B. and Lagarias, J. C.. On the distribution in short intervals of integers having no large prime factor. J. Number Theory, 25 (1987), 249–273.CrossRefGoogle Scholar
Ga.Gallagher, P. X.. Sieving by prime powers. Ada Arith., 24 (1974), 491–497.CrossRefGoogle Scholar
Go.Goetgheluck, P.. On prime divisors of binomial coefficients. Math. Comp., 51 (1988), 325–329.CrossRefGoogle Scholar
GK.Graham, S. W. and Kolesnik, G.. Van der Corput's Method of Exponential Sums (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
Gu.Guy, R. K.. Unsolved Problems in Number Theory, 2nd ed. (Springer-Verlag, New York, 1994).CrossRefGoogle Scholar
HR.Halberstam, H. and Richert, H.-E.. Sieve Methods (Academic Press, London, 1974).Google Scholar
J.Jutila, M.. On numbers with a large prime factor, II. J. Indian Math. Soc., 38 (1974), 125–130.Google Scholar
KP.Konyagin, S. and Pomerance, C.. Primes recognizable in deterministic polynomial time. To appear.Google Scholar
RS.Rosser, J. B. and Schoenfeld, L.. Approximate formulae for some functions of prime numbers. Ill. J. Math., 6 (1962), 64–94.Google Scholar
Sa1.Sander, J. W.. On prime power divisors of binomial coefficients. Bull. London Math. Soc., 24 (1992), 140–142.Google Scholar
Sa2.Sander, J. W.. Prime power divisors of binomial coefficients. J. reine angew. Math., 430 (1992), 1–20.Google Scholar
Sa3.Sander, J. W.. On primes not dividing binomial coefficients. Proc. Camb. Phil. Soc., 113 (1993), 225–232.Google Scholar
Sa4.Sander, J. W., e-mail correspondence (25th November 1994).Google Scholar
Sar.Sárközy, A.. On divisors of binomial coefficients. I. J. Number Theory, 20 (1985), 70–80.CrossRefGoogle Scholar
Sch.Schoenfeld, L.. Sharper bounds for the Chebyshev functions θ(x) and ψ(x), II. Math. Comp., 30 (1976), 337–360.Google Scholar
SW.Scheidler, R. and Williams, H. C.. A method of tabulating the number-theoretic function g(k). Math. Comp., 59 (1992), 251–257.Google Scholar
Ti.Titchmarsh., E. C.The Theory of the Riemann Zeta-function, 2nd ed., revised by D. R. Heath-Brown (Oxford University Press, New York, 1988).Google Scholar
Va.Vaaler, J. D.. Some extremal functions in Fourier analysis. Bull. Amer. Math. Soc., 12 (1985), 183–216.CrossRefGoogle Scholar
Ve.Velammal, G.. Is the binomial coefficient squarefree? Hardy-Ramanujan J., 18 (1995), 23–5.Google Scholar
W.Wirsing, E. A.. Multiple prime divisors of binomial coefficients. To appear.Google Scholar