Article contents
DYADIC SHIFT RANDOMIZATION IN CLASSICAL DISCREPANCY THEORY
Published online by Cambridge University Press: 06 May 2015
Abstract
Dyadic shifts 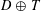 $D\oplus T$ of point distributions
$D\oplus T$ of point distributions  $D$ in the
$D$ in the 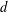 $d$-dimensional unit cube
$d$-dimensional unit cube 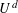 $U^{d}$ are considered as a form of randomization. Explicit formulas for the
$U^{d}$ are considered as a form of randomization. Explicit formulas for the 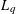 $L_{q}$-discrepancies of such randomized distributions are given in the paper in terms of Rademacher functions. Relying on the statistical independence of Rademacher functions, Khinchin’s inequalities, and other related results, we obtain very sharp upper and lower bounds for the mean
$L_{q}$-discrepancies of such randomized distributions are given in the paper in terms of Rademacher functions. Relying on the statistical independence of Rademacher functions, Khinchin’s inequalities, and other related results, we obtain very sharp upper and lower bounds for the mean 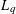 $L_{q}$-discrepancies,
$L_{q}$-discrepancies, 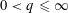 $0<q\leqslant \infty$. The upper bounds imply directly a generalization of the well-known Chen theorem on mean discrepancies with respect to dyadic shifts (Theorem 2.1). From the lower bounds, it follows that for an arbitrary
$0<q\leqslant \infty$. The upper bounds imply directly a generalization of the well-known Chen theorem on mean discrepancies with respect to dyadic shifts (Theorem 2.1). From the lower bounds, it follows that for an arbitrary 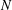 $N$-point distribution
$N$-point distribution 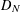 $D_{N}$ and any exponent
$D_{N}$ and any exponent 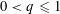 $0<q\leqslant 1$, there exist dyadic shifts
$0<q\leqslant 1$, there exist dyadic shifts 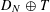 $D_{N}\oplus T$ such that the
$D_{N}\oplus T$ such that the 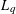 $L_{q}$-discrepancy
$L_{q}$-discrepancy 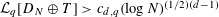 ${\mathcal{L}}_{q}[D_{N}\oplus T]>c_{d,q}(\log N)^{(1/2)(d-1)}$ (Theorem 2.2). The lower bounds for the
${\mathcal{L}}_{q}[D_{N}\oplus T]>c_{d,q}(\log N)^{(1/2)(d-1)}$ (Theorem 2.2). The lower bounds for the 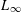 $L_{\infty }$-discrepancy are also considered in the paper. It is shown that for an arbitrary
$L_{\infty }$-discrepancy are also considered in the paper. It is shown that for an arbitrary 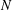 $N$-point distribution
$N$-point distribution 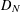 $D_{N}$, there exist dyadic shifts
$D_{N}$, there exist dyadic shifts 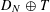 $D_{N}\oplus T$ such that
$D_{N}\oplus T$ such that 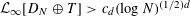 ${\mathcal{L}}_{\infty }[D_{N}\oplus T]>c_{d}(\log N)^{(1/2)d}$ (Theorem 2.3).
${\mathcal{L}}_{\infty }[D_{N}\oplus T]>c_{d}(\log N)^{(1/2)d}$ (Theorem 2.3).
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2015
References
- 4
- Cited by


