Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T09:31:43.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Detecting algebraic K-theory

Part of: Categories and geometry

Published online by Cambridge University Press:  26 February 2010

Victor Snaith
Victor Snaith
Affiliation:
The University of Western Ontario, London, Ontario, Canada, N6A 5B7.
Get access

Extract

Let l be a prime and let v ≥ 1 be an integer (when l = 2 we assume v ≥ 2). Any ring, A, with unit, possesses mod lv algebraic K-groups [B] denoted by Ki(A; Z/v) (i ≥ 0). For i ≥ 2, Ki(A; Z/lv) = [Pi(lv), BGLA +], the group of based homotopy classes of maps from the Moore space 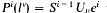, to BGLA+, the classifying space of algebraic K-theory [G–Q ; W].

MSC classification

Secondary: 18F25: Algebraic $K$-theory and $L$-theory
Type
Research Article
Information
Mathematika , Volume 31 , Issue 2 , December 1984 , pp. 234 - 244
Copyright
Copyright © University College London 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A.Adams, J. F.. Stable homotopy and generalised homology. Chicago University Lecture Notes in Mathematics (1974).Google Scholar
A-T.Araki, S. and Toda, H.. Multiplicative structures in mod q cohomology theories I, II. Osaka J. Math., 2 (1965), 71–1965, 3(1966), 81-120.Google Scholar
B.Browder, W.. Algebraic K-theory with coefficients Z/p. Springer-Verlag Lecture Notes in Mathematics, 65 (1978), 40–1978.CrossRefGoogle Scholar
D-F.Dwyer, W. G. and Friedlander, E. M.. Étale K-theory and arithmetic. Bull. Amer. Math. Soc (6), 3 (1982), 453–1982.CrossRefGoogle Scholar
D-F-S-T.Dwyer, W. G., Friedlander, E. M., Snaith, V. P. and Thomason, R. W.. Algebraic K-theory eventually surjects onto topological K-theory. Inventiones Math., 66 (1982), 481–1982.CrossRefGoogle Scholar
F.Friedlander, E. M.. Étale K-theory; I. Inv. Math., 60 (1980), 105–1980. II. To appear Ann Sci. Ec Norm. Sup.CrossRefGoogle Scholar
G-Q.Grayson, D. (after D. G. Quillen). Higher algebraic K-theory II. Springer-Verlag Lecture Notes in Mathematics 551,.217–240.CrossRefGoogle Scholar
Ma.May, J. P. (with contributions by Frank Quinn, Nigel Ray and Jorgen Tornehave). E∞ -ring spaces and E^-ring spectra. Springer-Verlag Lecture Notes in Mathematics, 577.Google Scholar
Ql.Quillen, D. G.. On the cohomology and K-theory of the general linear groups over a finite field. Annals of Math., 96 (1972), 552–1972.CrossRefGoogle Scholar
Q2.Quillen, D. G.. Higher algebraic K-theory I. Springer-Verlag Lecture Notes in Mathematics, 341, 77–139.Google Scholar
Snl.Snaith, V. P.. Unitary K-homology and the Lichtenbaum-Quillen conjecture on the algebraic K-theory of schemes. Springer-Verlag Lecture Notes in Mathematics, 1051 (1984), 128–1984.CrossRefGoogle Scholar
Sn2. Snaith, V. P.. Algebraic cobordism and K-theory. Mem. Amer. Math. Soc, 221 (1979).Google Scholar
Sn3. Snaith, V. P.. Algebraic K-theory and localised stable homotopy theory. Mem. Amer. Math. Soc, 280 (1983).Google Scholar
Sn4. Snaith, V. P.. A brief survey of Bott periodic algebraic K-theory. Current Trends in Alg. Top., Can. Math. Soc. Conf. Proc, 2(1), 37–42.Google Scholar
Sn5.Snaith, V. P.. Localised stable homotopy of some classifying spaces. Math. Proc. Camb. Phil. Soc, 89 (1981), 325–1981.CrossRefGoogle Scholar
Thl.Thomason, R. W.. Algebraic K-theory and etale cohomology. Preprint M.I.T. (1981).Google Scholar
Th2.Thomason, R. W.. The Lichtenbaum-Quillen conjecture for K/*[1/]. Current Trends in Alg. Top., Can. Math. Soc Conf. Proc, 2 (1), 117–1.Google Scholar
W.Wagoner, J. B.. Delooping the classifying spaces of algebraic K-theory. Topology, 11 (1972), 349–1972.CrossRefGoogle Scholar