Article contents
DENOMINATORS OF BERNOULLI POLYNOMIALS
Published online by Cambridge University Press: 16 April 2018
Abstract
For a positive integer  $n$ let
$n$ let 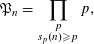 $$\begin{eqnarray}\mathfrak{P}_{n}=\mathop{\prod }_{\substack{ p \\ s_{p}(n)\geqslant p}}p,\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{P}_{n}=\mathop{\prod }_{\substack{ p \\ s_{p}(n)\geqslant p}}p,\end{eqnarray}$$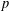 $p$ runs over primes and
$p$ runs over primes and 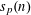 $s_{p}(n)$ is the sum of the base
$s_{p}(n)$ is the sum of the base 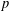 $p$ digits of
$p$ digits of  $n$. For all
$n$. For all  $n$ we prove that
$n$ we prove that 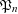 $\mathfrak{P}_{n}$ is divisible by all “small” primes with at most one exception. We also show that
$\mathfrak{P}_{n}$ is divisible by all “small” primes with at most one exception. We also show that 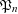 $\mathfrak{P}_{n}$ is large and has many prime factors exceeding
$\mathfrak{P}_{n}$ is large and has many prime factors exceeding 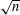 $\sqrt{n}$, with the largest one exceeding
$\sqrt{n}$, with the largest one exceeding 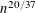 $n^{20/37}$. We establish Kellner’s conjecture that the number of prime factors exceeding
$n^{20/37}$. We establish Kellner’s conjecture that the number of prime factors exceeding 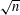 $\sqrt{n}$ grows asymptotically as
$\sqrt{n}$ grows asymptotically as 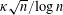 $\unicode[STIX]{x1D705}\sqrt{n}/\text{log}\,n$ for some constant
$\unicode[STIX]{x1D705}\sqrt{n}/\text{log}\,n$ for some constant  $\unicode[STIX]{x1D705}$ with
$\unicode[STIX]{x1D705}$ with 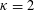 $\unicode[STIX]{x1D705}=2$. Further, we compare the sizes of
$\unicode[STIX]{x1D705}=2$. Further, we compare the sizes of 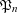 $\mathfrak{P}_{n}$ and
$\mathfrak{P}_{n}$ and 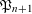 $\mathfrak{P}_{n+1}$, leading to the somewhat surprising conclusion that although
$\mathfrak{P}_{n+1}$, leading to the somewhat surprising conclusion that although 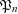 $\mathfrak{P}_{n}$ tends to infinity with
$\mathfrak{P}_{n}$ tends to infinity with  $n$, the inequality
$n$, the inequality 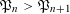 $\mathfrak{P}_{n}>\mathfrak{P}_{n+1}$ is more frequent than its reverse.
$\mathfrak{P}_{n}>\mathfrak{P}_{n+1}$ is more frequent than its reverse.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018
References
- 2
- Cited by


