Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T01:19:40.290Z Has data issue: false hasContentIssue false
  • English
  • Français

The class groups of quaternion and dihedral 2-groups

Published online by Cambridge University Press:  26 February 2010

A. Fröhlich ,
M. E. Keating  and
S. M. J. Wilson
A. Fröhlich
Affiliation:
King's College, London
M. E. Keating
Affiliation:
Imperial College, London
S. M. J. Wilson
Affiliation:
University of Durham
Get access

Extract

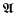Let be a = ℤ-order in A, a finite dimensional Q-algebra. K0(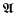) denotes the Grothendieck group of projective right 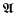-modules. 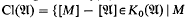locally isomorphic to 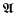} is a subgroup of K0(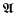) and is called the locally free classgroup o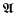f . (If 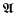= ℤΓ for some finite group Γ then 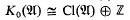as all ℤΓ projectives are locally free [12].)

Type
Research Article
Information
Mathematika , Volume 21 , Issue 1 , June 1974 , pp. 64 - 71
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bass., H.Algebraic K-theory (Benjamin).Google Scholar
2.Fröhlich, A.. “On the classgroup of integral grouprings of finite Abelian groups”, Mathematika, 16(1969), 143–152.CrossRefGoogle Scholar
3.Fröhlich, A. “On the classgroup of integral grouprings of finite Abelian groups II”, Mathematika, 19 (1972), 51–56.CrossRefGoogle Scholar
4.Frö, A. “Locally free modules over arithmetic orders”, to appear in Crelle.Google Scholar
5.Frö, A. “Arithmetic and Galois module structure for tame extensions”, to appear.Google Scholar
6.Frö, A.. “Artin Root numbers and Normal Integral Bases for Quaternion Fields”, Inv. Math., 17 (1972), 143–166.Google Scholar
7.Hasse, H.. Über die Klassenzahl Abelscher Zahlkörper (Berlin 1952, p. 29).CrossRefGoogle Scholar
8.Keating, M. E.. “On the AT-theory of the quaternion group”, to appear in Mathematika.Google Scholar
9.Keating, M. E.. “Whitehead groups of dihedral groups”, to appear.Google Scholar
10.Martinet, J.. “Modules Sur l' Algebre du Groupe Quaternionen”, Ann. Sci. de I'Ec. Norm-Sup. 4e serie, 4 (1971), 399–408.Google Scholar
11.Reiner, I. and Ullom, S.. “A Meyer-Vietoris sequence for class groups”, j. Alg. (to appear).Google Scholar
12.Swan, R. G.. “Induced representations and projective modules”, Ann. of Math. (2), 71 (1960), 552–578.CrossRefGoogle Scholar
13.Weber, H.. “Theorie der Abelscher Zahlk ö rper”, Acta Math., 8 (1886).CrossRefGoogle Scholar
14.Weber, H.. Lehrbuchder Algebren 2, 2nd edition —219–223,(1899).Google Scholar
15.Wilson, S. M. J.. “Reduced norms and the A-Theory of orders”, to appear.Google Scholar
16.Wilson, S. M. J.. “Twisted group rings and ramification”, to appear.Google Scholar