Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T05:56:31.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds on the covering radius of a lattice

Part of: Geometry of numbers

Published online by Cambridge University Press:  26 February 2010

Michel Deza  and
Viatcheslav Grishukhin
Michel Deza
Affiliation:
Department de Mathématiques et, Laboratoire d'Informatique, Eclo Normale Supérieure, 45 rue d'Ulm, 75230 Paris, cedex 05, France.
Viatcheslav Grishukhin
Affiliation:
CEMI RAN, Academy of Sciences of Russia, Krasikova 32, Moscow 117418, Russia.
Get access

Abstract

This paper depends on results of Baranovskii [1], [2]. The covering radius R(L) of an n-dimensional lattice L is the radius of smallest balls with centres at points of L which cover the whole space spanned by L. R(L) is closely related to minimal vectors of classes of the quotient 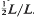. The convex hull of all minimal vectors of a class Q is a Delaunay polytope P(Q) of dimension ≤, dimension of L. Let 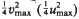be a maximal squared radius of P(Q) of dimension n (of dimension less than n, respectively). If 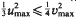, then 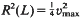. This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise, 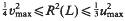. This is a refinement of a result of Norton ([3], Ch. 22).

MSC classification

Secondary: 11H31: Lattice packing and covering
Type
Research Article
Information
Mathematika , Volume 43 , Issue 1 , June 1996 , pp. 159 - 164
Copyright
Copyright © University College London 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baranovskii, E. P.. Subdivision of Euclidean spaces into L-polytopes of certain perfect lattices. Trudy Mat. Inst. Steklov, 196 (1991), 27–46 [ = Steklov Inst. Math., 196 (1992)].Google Scholar
2.Baranovskii, E. P.. The perfect lattices Γ(An), and the covering density of Γ(A9). Europ. J. Combinatorics, 15 (1994), 317–323.CrossRefGoogle Scholar
3.Conway, J. H. and Sloane, N. J. A.. Sphere Packings, Lattices and Groups, vol. 290 of Grundlagen der mathematischen Wissenshqften (Springer-Verlag, Berlin, 1987).Google Scholar