Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T05:45:20.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic formulas for the number of self-complementary graphs and digraphs

Published online by Cambridge University Press:  26 February 2010

Edgar M. Palmer
Edgar M. Palmer
Affiliation:
Michigan State University.
Get access

Extract

The number 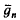of self-complementary graphs and the number 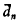of self-complementary digraphs were expressed by Read [4] in terms of cycle indexes of the appropriate pair groups. These formulas for 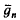and 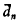, together with a modification of the method employed by Oberschelp [3] for graphs, can be used to obtain estimates for 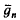and 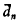and a bound on the error. For graph theoretic definitions not given here, we refer to the book [2].

Type
Research Article
Information
Mathematika , Volume 17 , Issue 1 , June 1970 , pp. 85 - 90
Copyright
Copyright © University College London 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bruijn, N. G. de, “Polya's theory of counting”, Applied combinatorial mathematics, Beckenbach, E. F., ed. (John Wiley and Sons, New York, 1964).Google Scholar
2.Harary, F., Graph theory (Addison-Wesley, Reading, Mass., 1969).CrossRefGoogle Scholar
3.Oberschelp, W., “Kombinatorische Anzahlbestimmungen in Relationen”, Math. Ann., 174 (1967), 53–78.CrossRefGoogle Scholar
4.Read, R. C., “On the number of self-complementary graphs and digraphs”, J. London Math. Soc., 38 (1963), 99–104.CrossRefGoogle Scholar