Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T11:33:42.946Z Has data issue: false hasContentIssue false
  • English
  • Français

An integral-geometric meaning for lower order area functions of convex bodies

Part of: General convexity Classical measure theory

Published online by Cambridge University Press:  26 February 2010

William J. Firey
William J. Firey
Affiliation:
Oregon State University, Corvallis, Oregon, U.S.A.
Get access

Extract

Integral geometry is the study of measures of sets of geometric figures. Commonly a measure of this sort is an integral of a density or differential form; the density is determined by the type of figure, but is independent of the particular set of such figures to which the measure is assigned. As one of the simplest examples, the area of a plane convex point set K is the integral over K of the density dx dy for points with Cartesian co-ordinates x, y. But when we assign a Hausdorff linear measure to the set of boundary points of K, we obtain a measure of quite another sort. This is representable as a Stieltjes integral of arc length density; here the density depends on the choice of K. The examples suggest examining measures for other sets of figures, where each such set 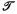is made up of all those figures from a certain class which support, in some sense, a convex body. Further, the examples lead us to expect that measures of this kind will appear as integrals of densities which may depend on the choices of 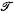. Here we treat a question of the type just described: to determine a measure for sets of q–flats which support a convex body.

MSC classification

Secondary: 28A75: Length, area, volume, other geometric measure theory 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Type
Research Article
Information
Mathematika , Volume 19 , Issue 2 , December 1972 , pp. 205 - 212
Copyright
Copyright © University College London 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Blaschke, W., Integralgeometrie (Paris, 1935).Google Scholar
2.Bonnesen, T. and Fenchel, W., Theorie der konvexen Körper (Berlin, 1934).Google Scholar
3.Fenchel, W. and Jessen, B., “Mengenfunktionen und konvexe Körper”, Det Kgl. Danske Videnskab. Selskab, Mat.-fys. Medd., 16 (1938), 3.Google Scholar
4.Firey, W., “Local behaviour of area functions of convex bodies”, Pacific J. Math., 35 (1970), 345–357.CrossRefGoogle Scholar
5.Flanders, H., Differential forms (New York, 1963).Google Scholar
6.Hadwiger, H., Vorlesungen überlnhalt, Oberfläche und Isoperimetrie (Berlin-Göttingen-Heidelberg, 1957).CrossRefGoogle Scholar
7.Kowalewski, G., Einführung in die Determinantentheorie, 3rd ed. (Berlin, 1942).Google Scholar
8.Maak, W., “Oberflächenintegral und Stokes Formel im gewöhnlichen Raume”, Math. Ann., 116 (1939), 574–597.CrossRefGoogle Scholar
9.Petkantschin, B., “Zusammenhänge zwischen den Dichten der linearen Unterräume in n–dimensionalen Raum”, Abh. Math. Sem. Hans. Hamburg, 11 (1936) 249–310.CrossRefGoogle Scholar
10.Santaló, L., Introduction to Integral Geometry (Paris, 1953).Google Scholar
11.Zelver, J., The integro-geometric tangent measures of Euclidean n-space, Ph.D. Thesis, Oregon State University, (Corvallis, 1970).Google Scholar