Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T01:18:49.914Z Has data issue: false hasContentIssue false
  • English
  • Français

ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY

Part of: Limit theorems Diophantine approximation, transcendental number theory Sequences and sets Designs and configurations

Published online by Cambridge University Press:  19 June 2018

Thomas F. Bloom ,
Sam Chow ,
Ayla Gafni  and
Aled Walker
Thomas F. Bloom
Affiliation:
Heilbronn Institute for Mathematical Research, Department of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, U.K. email [email protected]
Sam Chow
Affiliation:
Department of Mathematics, University of York, Heslington, York YO10 5DD, U.K. email [email protected]
Ayla Gafni
Affiliation:
Department of Mathematics, 915 Hylan Building, University of Rochester, Rochester, NY 14627, U.S.A. email [email protected]
Aled Walker
Affiliation:
Andrew Wiles Building, University of Oxford, Radcliffe Observatory Quarter, Woodstock Rd, Oxford OX2 6GG, U.K. email [email protected]
Get access

Abstract

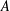Let $A$ be a set of natural numbers. Recent work has suggested a strong link between the additive energy of 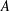$A$ (the number of solutions to 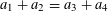$a_{1}+a_{2}=a_{3}+a_{4}$ with 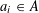$a_{i}\in A$) and the metric Poissonian property, which is a fine-scale equidistribution property for dilates of 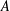$A$ modulo 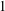$1$. There appears to be reasonable evidence to speculate a sharp Khinchin-type threshold, that is, to speculate that the metric Poissonian property should be completely determined by whether or not a certain sum of additive energies is convergent or divergent. In this article, we primarily address the convergence theory, in other words the extent to which having a low additive energy forces a set to be metric Poissonian.

MSC classification

Primary: 11J71: Distribution modulo one 11J83: Metric theory 05B10: Difference sets (number-theoretic, group-theoretic, etc.) 11B30: Arithmetic combinatorics; higher degree uniformity 60F10: Large deviations
Type
Research Article
Information
Mathematika , Volume 64 , Issue 3 , 2018 , pp. 679 - 700
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aistleitner, C., Berkes, I. and Seip, K., GCD sums from Poisson integrals and systems of dilated functions. J. Eur. Math. Soc. (JEMS) 017 2015, 1517–1546.Google Scholar
Aistleitner, C., Larcher, G. and Lewko, M., Additive energy and the Hausdorff dimension of the exceptional set in metric pair correlation problems, with an appendix by J. Bourgain. Israel J. Math. 222 2017, 463–485.Google Scholar
Alon, N. and Spencer, J., The Probabilistic Method, 3rd edn., Wiley (Hoboken, NJ, 2008).Google Scholar
Bondarenko, A. and Seip, K., GCD sums and complete sets of square-free numbers. Bull. Lond. Math. Soc. 47 2015, 29–41.Google Scholar
Bondarenko, A. and Seip, K., Large greatest common divisor sums and extreme values of the Riemann zeta function. Duke Math. J. 166 2017, 1685–1701.Google Scholar
Gál, I. S., A theorem concerning Diophantine approximations. Nieuw Arch. Wiskunde 23 1949, 13–38.Google Scholar
Harman, G., Metric Number Theory (London Mathematical Society Monographs. New Series 18 ), The Clarendon Press, Oxford University Press (New York, 1998).Google Scholar
Lachmann, T. and Technau, N., On exceptional sets in the metric Poissonian pair correlations problem, Preprint, 2017, arXiv:1708.08599.Google Scholar
Lewko, M. and Radziwiłł, M., Refinements of Gál’s theorem and applications. Adv. Math. 305 2017, 280–297.Google Scholar
Marklof, J., Distribution modulo one and Ratner’s theorem. In Equidistribution in Number Theory, An Introduction, 217–244 (NATOS cience Series II: Mathematics, Physics and Chemistry 237 ), Springer (Dordrecht, 2007).Google Scholar
Rudnick, Z. and Sarnak, P., The pair correlation function of fractional parts of polynomials. Comm. Math. Phys. 194 1998, 61–70.Google Scholar
Rudnick, Z. and Zaharescu, A., A metric result on the pair correlation of fractional parts of sequences. Acta Arith. 89 1999, 283–293.Google Scholar
Schmidt, W., A metrical theorem in Diophantine approximation. Canad. J. Math. 12 1960, 619–631.Google Scholar
Walker, A., The primes are not metric Poissonian. Mathematika 64 2018, 230–236.Google Scholar