Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T19:56:28.728Z Has data issue: false hasContentIssue false
  • English
  • Français

Triposes as a generalization of localic geometric morphisms

Published online by Cambridge University Press:  29 January 2021

Jonas Frey  and
Thomas Streicher Open the ORCID record for Thomas Streicher [Opens in a new window]
Jonas Frey
Affiliation:
Department of Philosophy, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Thomas Streicher*
Affiliation:
Fachbereich Mathematik, Technische Universität Darmstadt, Darmstadt, Germany
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In Hyland et al. (1980), Hyland, Johnstone and Pitts introduced the notion of tripos for the purpose of organizing the construction of realizability toposes in a way that generalizes the construction of localic toposes from complete Heyting algebras. In Pitts (2002), one finds a generalization of this notion eliminating an unnecessary assumption of Hyland et al. (1980). The aim of this paper is to characterize triposes over a base topos 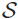${\cal S}$ in terms of so-called constant objects functors from 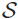${\cal S}$ to some elementary topos. Our characterization is slightly different from the one in Pitts’s PhD Thesis (Pitts, 1981) and motivated by the fibered view of geometric morphisms as described in Streicher (2020). In particular, we discuss the question whether triposes over Set giving rise to equivalent toposes are already equivalent as triposes.

Keywords

Fibered categoriestriposestoposes
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 31 , Special Issue 9: In Homage to Martin Hofmann , October 2021 , pp. 1024 - 1033
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bénabou, J. (1974). Logique Catégorique, Lecture Notes of a Course at University, Montreal.Google Scholar
Bénabou, J. (1980). Des Catégories Fibrées, Handwritten Lecture Notes by J.-R. Roisin of a course at Univ. Louvain-la-Neuve.Google Scholar
Frey, J. (2013). A Fibrational Study of Realizability Toposes. Thesis University, Paris 7. arXiv:1403.3672.Google Scholar
Hyland, M., Johnstone, P. and Pitts, A. (1980). Tripos theory. Mathematical Proceedings of the Cambridge Philosophical Society 88 (2) 205–232.10.1017/S0305004100057534CrossRefGoogle Scholar
Jibladze, M. (1989). Geometric morphisms and indexed toposes. In: Categorical Topology and its Relation to Analysis, Algebra and Combinatorics (Prague, 1988), World Scientific Publications, 10–18.Google Scholar
Johnstone, P. T. (1977). Topos Theory, Academic Press, New York.Google Scholar
Miquel, A. (2020a). Implicative algebras: A new foundation for realizability and forcing. Mathematical Structures in Computer Science 30 (5) 458–510.10.1017/S0960129520000079CrossRefGoogle Scholar
Miquel, A. (2020b). Implicative Algebras II: Completeness w.r.t. Set-based Triposes. arXiv:2011.09085.Google Scholar
Pitts, A. (1981). The Theory of Triposes, Thesis University of Cambridge.Google Scholar
Pitts, A. (2002). Tripos theory in retrospect. Mathematical Structures in Computer Science 12 (3) 265–279.10.1017/S096012950200364XCrossRefGoogle Scholar
Streicher, T. (2020). Fibered Categories à la Jean Bénabou. arXiv:1801.02927Google Scholar
van Oosten, J. (2008). Realizability. An Introduction to its Categorical Side, Elsevier.Google Scholar