Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-18T08:25:10.705Z Has data issue: false hasContentIssue false
  • English
  • Français

A stable universal domain related to 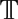$\mathbb{T}$ω

Published online by Cambridge University Press:  22 May 2015

HAORAN ZHAO  and
HUI KOU
HAORAN ZHAO
Affiliation:
School of Mathematics, Sichuan University, Chengdu 610064, P. R. China Email: [email protected]
HUI KOU
Affiliation:
School of Mathematics, Sichuan University, Chengdu 610064, P. R. China Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1978, G. Plotkin noticed that 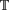$\mathbb{T}$ω, the cartesian product of ω copies of the three element flat domain of Booleans, is a universal domain, where ‘universal’ means that the retracts of 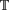$\mathbb{T}$ω for Scott's continuous semantics are exactly all the ωCC-domains, which with Scott continuous functions form a cartesian closed category. As usual, ‘ω’ is for ‘countably based,’ and here ‘CC’ is for ‘conditionally complete,’ which essentially means that any subset which is pairwise bounded has a least upper bound. Since 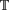$\mathbb{T}$ω is also an ωDI-domain (an important structure in stable domain theory), the following problem arises naturally: is there a cartesian closed category C of domains with stable functions such that 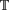$\mathbb{T}$ω, or a related structure, is universal in C for Berry’s stable semantics? The aim of this paper is to answer this question. We first investigate the properties of stable retracts. We introduce a new class of domains called conditionally complete DI-domains (CCDI-domain for short) and show that, (1) 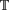$\mathbb{T}$ω is an ωCCDI-domain and the category of CCDI-domains (resp. ωCCDI-domains) with stable functions is cartesian closed; (2) [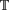$\mathbb{T}$ω →st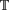$\mathbb{T}$ω] is a stable universal domain in the sense that every ωCCDI-domain is a stable retract of [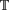$\mathbb{T}$ω → st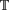$\mathbb{T}$ω], where [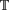$\mathbb{T}$ω → st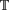$\mathbb{T}$ω] is the stable function space of 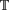$\mathbb{T}$ω; (3) in particular, [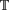$\mathbb{T}$ω → st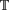$\mathbb{T}$ω] is not a stable retract of 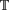$\mathbb{T}$ω and hence 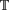$\mathbb{T}$ω is not universal for Berry’s stable semantics. We remark that this paper is a completion and correction of our earlier report in the Proceedings of the 6th International Symposium on Domain Theory and Its Applications (ISDT2013).

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Special Issue 4: Symposium on Domain Theory (ISDT 2013) , May 2017 , pp. 540 - 556
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramsky, S. and Jung, A. (1994). Domain theory. In: Abramsky, S., Gabbay, D.M. and Maibaum, T.S.E. (eds.) Semantic Structures, Handbook of Logic in Computer Science, volume 3, Clarendon Press 1–168.Google Scholar
Amadio, R. (1991). Bifinite domains: Stable case. In: Pitt, D.H. et al. (eds.) Category Theory and Computer Science. Springer Lecture Notes in Computer Sciences 530, 16–33.CrossRefGoogle Scholar
Amadio, R. and Curien, P.L. (1998). Domains and Lambda Calculi, Cambridge Tracts in Theoretical Computer Science, volume 46, Cambridge University Press.Google Scholar
Barendregt, H. and Koymans, K. (1980). Comparing some class of lambda-calculus models. In: Seldin, J.P. and Hindley, J.R. (eds.) To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, Academic Press 287–301.Google Scholar
Barendregt, H. and Longo, G. (1980). Equality of λ-terms in the model Tω . In: To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, Academic Press.Google Scholar
Berry, G. (1978). Stable models of typed λ-calculi. In: Proceedings of the 5th International Colloquium on Automata, Languages and Programming. Springer Verlag Lecture Notes in Computer Science 62 72–89.Google Scholar
Chen, Y. and Jung, A. (2006). A logical approach to stable domains. Theoretical Computer Science 368 (1–2) 124–148.CrossRefGoogle Scholar
Droste, M. and Göbel, R. (1991). Universal information systems. International Journal of Foundations of Computer Science 1 (4) 413–424.Google Scholar
Droste, M. and Göbel, R. (1993). Universal domains and the amalgamation property. Mathematical Structures in Computer Science 3 (2) 137–159.CrossRefGoogle Scholar
Gierz, G., Hofmann, K.H., Keimel, K., Lawson, J.D., Mislove, M. and Scott, D.S. (2003). Continuous Lattices and Domains, Encyclopedia of Mathematics and its Applications volume 93, Cambridge University Press.Google Scholar
Gunter, C. and Jung, A. (1990). Coherence and consistency in domains. Journal of Pure and Applied Algebra 63 (1) 49–66.Google Scholar
Kanneganti, R. (1995). Universal domains for sequential computation. PhD thesis, Rice University.Google Scholar
Melliès, P.-A. (2005). Sequential algorithms and strongly stable functions. Theoretical Computer Science 343 (1–2) 237–281.Google Scholar
Plotkin, G.D. (1978). $\mathbb{T}$ ω as a universal domain. J. Computer and System Sciences 17 (2) 209–236.Google Scholar
Scott, D.S. (1976). Data types as lattices. SIAM J. Computing 5 (3) 522–587.CrossRefGoogle Scholar
Taylor, P. (1990). An algebraic approach to stable domains. Pure and Applied Algebra 64 (2) 171–203.Google Scholar
Zhang, G.-Q. (1992). DI-domains as prime information systems. Information and Computation 100 (2) 151–177.CrossRefGoogle Scholar
Zhang, G.-Q. (1996). The largest cartesian closed category of stable domains. Theoretical Computer Science 166 (1–2) 203–219.Google Scholar
Zhao, H. and Kou, H. (2014). $\mathbb{T}$ ω as a stable universal domain. In: Liu, Y.-M., Luo, M.-K., Mislove, M. and Zhang, G.-Q. (eds.) Proceedings of the 6th International Symposium on Domain Theory and Its Applications (ISDT 2014). Electronic Notes in Theoretical Computer Science 301 189–202.Google Scholar