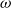1. Introduction
The main contribution of this paper is relating robust analyses and Scott-continuous maps (between
![]() $\omega$
-continuous lattices). This contribution is relevant to the broader endeavor of developing software tools for system analysis based on mathematical models. Typically, the behavior of a controlled system is given a priori, but for most systems the open system approach is insufficient as the correctness of the controlling system depends on properties of the environment. This requires modeling the environment as well. Software tools (for system analysis) manipulate formal descriptions. The key point of formal descriptions is their mathematical exactness. However, exactness should not be confused with precision. In particular, mathematical descriptions should make explicit known unknowns and the amount of imprecision. There are two unavoidable sources of imprecision: errors in measurements (on physical systems) and representations of continuous quantities in software tools.
$\omega$
-continuous lattices). This contribution is relevant to the broader endeavor of developing software tools for system analysis based on mathematical models. Typically, the behavior of a controlled system is given a priori, but for most systems the open system approach is insufficient as the correctness of the controlling system depends on properties of the environment. This requires modeling the environment as well. Software tools (for system analysis) manipulate formal descriptions. The key point of formal descriptions is their mathematical exactness. However, exactness should not be confused with precision. In particular, mathematical descriptions should make explicit known unknowns and the amount of imprecision. There are two unavoidable sources of imprecision: errors in measurements (on physical systems) and representations of continuous quantities in software tools.
The key feature of robust analyses is the ability to cope with small amounts of imprecision. On the other hand, analyses can be implemented in software tools only if they are computable. A definition of computability for effectively given domains has been proposed in Smyth (Reference Smyth1977, Definition 3.1), where the domains considered include those of interest for us, namely
![]() $\omega$
-continuous lattices. The key point of this, and similar proposals, is that computable maps (between effectively given domains) are necessarily Scott continuous.
$\omega$
-continuous lattices. The key point of this, and similar proposals, is that computable maps (between effectively given domains) are necessarily Scott continuous.
For the benefit of readers, before outlining the main result of the paper, we review the context in which it is placed and recall related results, while keeping technicalities to a minimum.
Systems
First, one has to decide how to model systems. The simplest systems, i.e., discrete systems, can be modeled by a set
![]() $\mathbb{S}$
(of states) and a transition map
$\mathbb{S}$
(of states) and a transition map
![]() $t:\mathbb{S} \to \mathbb{S}$
describing the deterministic state change of the system in one step. The systems we consider are closed, i.e., they do not interact with the environment, or to put it differently, a model should account also for the environment. In this respect, it is important to model also known unknowns (for discrete systems, imprecision is not an issue). The simplest way to do this is by non-determinism, namely a state in
$t:\mathbb{S} \to \mathbb{S}$
describing the deterministic state change of the system in one step. The systems we consider are closed, i.e., they do not interact with the environment, or to put it differently, a model should account also for the environment. In this respect, it is important to model also known unknowns (for discrete systems, imprecision is not an issue). The simplest way to do this is by non-determinism, namely a state in
![]() $\mathbb{S}$
is replaced by a set of states and the transition map is replaced by a transition relation
$\mathbb{S}$
is replaced by a set of states and the transition map is replaced by a transition relation
![]() $T\subseteq\mathbb{S}\times\mathbb{S}$
. In theoretical computer science, the pair
$T\subseteq\mathbb{S}\times\mathbb{S}$
. In theoretical computer science, the pair
![]() $(\mathbb{S},T)$
is called a transition system.
$(\mathbb{S},T)$
is called a transition system.
Analyses
We move from the category of sets and relations to the category of complete lattices and monotonic maps. More precisely, we replace
![]() $\mathbb{S}$
with the complete lattice
$\mathbb{S}$
with the complete lattice
![]() $\mathbb{P}(\mathbb{S})$
of subsets of
$\mathbb{P}(\mathbb{S})$
of subsets of
![]() $\mathbb{S}$
, and a relation
$\mathbb{S}$
, and a relation
![]() $T\subseteq\mathbb{S}\times\mathbb{S}'$
with the monotonic map
$T\subseteq\mathbb{S}\times\mathbb{S}'$
with the monotonic map
![]() $T_*:\mathbb{P}(\mathbb{S}) \to \mathbb{P}(\mathbb{S}')$
such that:
$T_*:\mathbb{P}(\mathbb{S}) \to \mathbb{P}(\mathbb{S}')$
such that:
We take reverse inclusion as the partial order
![]() $\leq$
on
$\leq$
on
![]() $\mathbb{P}(\mathbb{S})$
, i.e.,
$\mathbb{P}(\mathbb{S})$
, i.e.,
![]() $S'\leq S\iff S'\supseteq S$
. The rationale for this choice is that a smaller set (of states) provides more information on the actual state of the system, because it constitutes a more accurate approximation of the state. The transition relations on
$S'\leq S\iff S'\supseteq S$
. The rationale for this choice is that a smaller set (of states) provides more information on the actual state of the system, because it constitutes a more accurate approximation of the state. The transition relations on
![]() $\mathbb{S}$
form a complete lattice
$\mathbb{S}$
form a complete lattice
![]() $\mathbb{P}(\mathbb{S}\times\mathbb{S})$
, where
$\mathbb{P}(\mathbb{S}\times\mathbb{S})$
, where
![]() $T'\leq T$
means that T is more deterministic than T’.
$T'\leq T$
means that T is more deterministic than T’.
Several analyses correspond to monotonic maps between complete lattices. For instance, reachability analysis for transition systems on
![]() $\mathbb{S}$
corresponds to the map
$\mathbb{S}$
corresponds to the map
![]() $R:\mathbb{P}(\mathbb{S}\times\mathbb{S})\times\mathbb{P}(\mathbb{S})\to \mathbb{P}(\mathbb{S})$
given by
$R:\mathbb{P}(\mathbb{S}\times\mathbb{S})\times\mathbb{P}(\mathbb{S})\to \mathbb{P}(\mathbb{S})$
given by
![]() $R(T,I)\stackrel{\triangle}{=} T^*(I)$
, i.e., the set of states reachable in a finite number of steps from (a state in) I, while safety analysis corresponds to the map
$R(T,I)\stackrel{\triangle}{=} T^*(I)$
, i.e., the set of states reachable in a finite number of steps from (a state in) I, while safety analysis corresponds to the map
![]() $S:\mathbb{P}(\mathbb{S}\times\mathbb{S})\times\mathbb{P}(\mathbb{S})\times\mathbb{P}(\mathbb{S})\to \Sigma$
in which
$S:\mathbb{P}(\mathbb{S}\times\mathbb{S})\times\mathbb{P}(\mathbb{S})\times\mathbb{P}(\mathbb{S})\to \Sigma$
in which
![]() $\Sigma$
is the two-point lattice
$\Sigma$
is the two-point lattice
![]() $\bot<\top$
and
$\bot<\top$
and
![]() $S(T,I,E)=\top\stackrel{\triangle}{\iff} T^*(I)\cap E=\emptyset$
, i.e., no bad state in E is reachable from I.
$S(T,I,E)=\top\stackrel{\triangle}{\iff} T^*(I)\cap E=\emptyset$
, i.e., no bad state in E is reachable from I.
Approximation
The partial order on a complete lattice X allows (qualitative) comparisons, in particular, we say that x’ is an over-approximation of x when
![]() $x'\leq x$
. The category of complete lattices and monotonic maps is also the natural setting for abstract interpretation (Cousot, Reference Cousot1996; Cousot and Cousot, Reference Cousot and Cousot1977). More precisely, given an interpretation
$x'\leq x$
. The category of complete lattices and monotonic maps is also the natural setting for abstract interpretation (Cousot, Reference Cousot1996; Cousot and Cousot, Reference Cousot and Cousot1977). More precisely, given an interpretation
![]() ${{\left[\!\left[ - \right]\!\right]}}$
of a (programming) language in a complete lattice X, one can choose another complete lattice
${{\left[\!\left[ - \right]\!\right]}}$
of a (programming) language in a complete lattice X, one can choose another complete lattice
![]() $X_a$
related to X by an adjunction
$X_a$
related to X by an adjunction
![]() i.e., a pair of monotonic maps
i.e., a pair of monotonic maps
![]() $\alpha$
(called abstraction) and
$\alpha$
(called abstraction) and
![]() $\gamma$
(called concretization) such that
$\gamma$
(called concretization) such that
![]() $x'\leq_a\alpha(x)\iff\gamma(x')\leq x$
. In general,
$x'\leq_a\alpha(x)\iff\gamma(x')\leq x$
. In general,
![]() $X_a$
is simpler than X (e.g.,
$X_a$
is simpler than X (e.g.,
![]() $X_a$
can be finite) and allows interpretations
$X_a$
can be finite) and allows interpretations
![]() ${{\left[\!\left[ - \right]\!\right]}}_a$
of the language for computing over-approximations of
${{\left[\!\left[ - \right]\!\right]}}_a$
of the language for computing over-approximations of
![]() ${{\left[\!\left[ - \right]\!\right]}}$
, i.e.,
${{\left[\!\left[ - \right]\!\right]}}$
, i.e.,
![]() $\gamma({{\left[\!\left[ p \right]\!\right]}}_a)\leq{{\left[\!\left[ p \right]\!\right]}}$
for every (program) p in the language.
$\gamma({{\left[\!\left[ p \right]\!\right]}}_a)\leq{{\left[\!\left[ p \right]\!\right]}}$
for every (program) p in the language.
The adjunction between
![]() $X_a$
and X gives a systematic way of defining a
$X_a$
and X gives a systematic way of defining a
![]() ${{\left[\!\left[ - \right]\!\right]}}_a$
from
${{\left[\!\left[ - \right]\!\right]}}_a$
from
![]() ${{\left[\!\left[ - \right]\!\right]}}$
. For instance, if the language is given by the BNF
${{\left[\!\left[ - \right]\!\right]}}$
. For instance, if the language is given by the BNF
![]() $p::=c \mid f(p)$
, then an interpretation
$p::=c \mid f(p)$
, then an interpretation
![]() ${{\left[\!\left[ - \right]\!\right]}}$
in X is uniquely determined by
${{\left[\!\left[ - \right]\!\right]}}$
in X is uniquely determined by
![]() ${{\left[\!\left[ c \right]\!\right]}} \in X$
and a monotonic map
${{\left[\!\left[ c \right]\!\right]}} \in X$
and a monotonic map
![]() ${{\left[\!\left[ f \right]\!\right]}}:X\to X$
, and the abstract interpretation (computing over-approximations) in
${{\left[\!\left[ f \right]\!\right]}}:X\to X$
, and the abstract interpretation (computing over-approximations) in
![]() $X_a$
is determined by taking
$X_a$
is determined by taking
![]() ${{\left[\!\left[ c \right]\!\right]}}_a\stackrel{\triangle}{=}\alpha({{\left[\!\left[ c \right]\!\right]}}) \in X_a$
and
${{\left[\!\left[ c \right]\!\right]}}_a\stackrel{\triangle}{=}\alpha({{\left[\!\left[ c \right]\!\right]}}) \in X_a$
and
![]() ${{\left[\!\left[ f \right]\!\right]}}_a\stackrel{\triangle}{=}\alpha\circ{{\left[\!\left[ f \right]\!\right]}}\circ\gamma:X_a\to X_a$
. In static analysis, the choice of
${{\left[\!\left[ f \right]\!\right]}}_a\stackrel{\triangle}{=}\alpha\circ{{\left[\!\left[ f \right]\!\right]}}\circ\gamma:X_a\to X_a$
. In static analysis, the choice of
![]() $X_a$
and
$X_a$
and
![]() ${{\left[\!\left[ - \right]\!\right]}}_a$
is a matter of trade-offs between the cost of computing
${{\left[\!\left[ - \right]\!\right]}}_a$
is a matter of trade-offs between the cost of computing
![]() ${{\left[\!\left[ p \right]\!\right]}}_a$
and the information provided by
${{\left[\!\left[ p \right]\!\right]}}_a$
and the information provided by
![]() $\gamma({{\left[\!\left[ p \right]\!\right]}}_a)$
.
$\gamma({{\left[\!\left[ p \right]\!\right]}}_a)$
.
Spaces
To model more complex systems, e.g., continuous or hybrid (Goebel et al., Reference Goebel, Sanfelice and Teel2009), one may have to replace sets with more complex spaces. For instance, in Moggi et al. (Reference Moggi, Farjudian, Duracz and Taha2018), hybrid systems were modeled by triples
![]() $(\mathbb{S},F,G)$
, where
$(\mathbb{S},F,G)$
, where
![]() $\mathbb{S}$
is a Banach space, and F and G are binary relations on
$\mathbb{S}$
is a Banach space, and F and G are binary relations on
![]() $\mathbb{S}$
—called flow and jump relation, respectively—which constrain how the system may evolve continuously (in time) and discontinuously (instantaneously). As in transition systems, the relations F and G allow modeling known unknowns. Despite the increased complexity of models, it is still possible and useful to move to the category of complete lattices and monotonic maps and use it for analyses and abstract interpretations of these more complex systems.
$\mathbb{S}$
—called flow and jump relation, respectively—which constrain how the system may evolve continuously (in time) and discontinuously (instantaneously). As in transition systems, the relations F and G allow modeling known unknowns. Despite the increased complexity of models, it is still possible and useful to move to the category of complete lattices and monotonic maps and use it for analyses and abstract interpretations of these more complex systems.
Imprecision
In defining reachability for hybrid systems, we realized the need to cope with imprecision, see also Fränzle (Reference Fränzle1999). Thus, in Moggi et al. (Reference Moggi, Farjudian, Duracz and Taha2018), we introduced safe and robust reachability analysis. In Moggi et al. (Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019), we used metric spaces to formalize the notions of imprecision and robust analysis. In a metric space
![]() $\mathbb{S}$
, a level of imprecision
$\mathbb{S}$
, a level of imprecision
![]() $\delta>0$
means that one cannot distinguish two points s and s’ when their distance d(s,s’) is less than
$\delta>0$
means that one cannot distinguish two points s and s’ when their distance d(s,s’) is less than
![]() $\delta$
. If one considers subsets instead of points, and allows
$\delta$
. If one considers subsets instead of points, and allows
![]() $\delta$
to become arbitrarily small, then one cannot distinguish two subsets that have the same closure, namely
$\delta$
to become arbitrarily small, then one cannot distinguish two subsets that have the same closure, namely
![]() $\forall \delta>0.B(S,\delta)=B(\overline{S},\delta)$
, where
$\forall \delta>0.B(S,\delta)=B(\overline{S},\delta)$
, where
![]() $B(S,\delta)$
is the open subset
$B(S,\delta)$
is the open subset
![]() $\{s' \mid \exists s \in S.d(s,s')<\delta\}$
and the closure
$\{s' \mid \exists s \in S.d(s,s')<\delta\}$
and the closure
![]() $\overline{S}$
is the smallest closed subset containing S. Therefore, one can replace
$\overline{S}$
is the smallest closed subset containing S. Therefore, one can replace
![]() $\mathbb{P}(\mathbb{S})$
with the complete lattice
$\mathbb{P}(\mathbb{S})$
with the complete lattice
![]() $\mathbb{C}(\mathbb{S})$
of closed subsets, which is related to the former by the adjunction
$\mathbb{C}(\mathbb{S})$
of closed subsets, which is related to the former by the adjunction
![]() with
with
![]() $\gamma$
an inclusion map and
$\gamma$
an inclusion map and
![]() $\alpha$
a surjective map. This replacement is convenient, since the cardinality of
$\alpha$
a surjective map. This replacement is convenient, since the cardinality of
![]() $\mathbb{C}(\mathbb{S})$
can be smaller than that of
$\mathbb{C}(\mathbb{S})$
can be smaller than that of
![]() $\mathbb{P}(\mathbb{S})$
, e.g., when
$\mathbb{P}(\mathbb{S})$
, e.g., when
![]() $\mathbb{S}$
is the real line
$\mathbb{S}$
is the real line
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
Robustness
A monotonic map
![]() $A:\mathbb{P}(\mathbb{S})\to \mathbb{P}(\mathbb{S}')$
, with
$A:\mathbb{P}(\mathbb{S})\to \mathbb{P}(\mathbb{S}')$
, with
![]() $\mathbb{S}$
and
$\mathbb{S}$
and
![]() $\mathbb{S}'$
metric spaces, is robust when small input changes cause small output changes, i.e.,
$\mathbb{S}'$
metric spaces, is robust when small input changes cause small output changes, i.e.,
When A is robust, there is no loss of information in restricting to closed subsets, namely there exists a unique monotonic map
![]() $A_c:\mathbb{C}(\mathbb{S})\to \mathbb{C}(\mathbb{S}')$
such that
$A_c:\mathbb{C}(\mathbb{S})\to \mathbb{C}(\mathbb{S}')$
such that
![]() $A_c\circ\alpha=\alpha\circ A$
. Thus, the focus of Moggi et al. (Reference Moggi, Farjudian, Duracz and Taha2018, Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019) was on analyses between complete lattices of closed subsets. In Moggi et al. (Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019), sufficient (and almost necessary) conditions were identified to ensure that every monotonic map
$A_c\circ\alpha=\alpha\circ A$
. Thus, the focus of Moggi et al. (Reference Moggi, Farjudian, Duracz and Taha2018, Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019) was on analyses between complete lattices of closed subsets. In Moggi et al. (Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019), sufficient (and almost necessary) conditions were identified to ensure that every monotonic map
![]() $A\,:\,\mathbb{C}(\mathbb{S})\to \mathbb{C}(\mathbb{S}')$
has a best robust approximation, i.e., the biggest robust map
$A\,:\,\mathbb{C}(\mathbb{S})\to \mathbb{C}(\mathbb{S}')$
has a best robust approximation, i.e., the biggest robust map
![]() $\Box_R(A): \mathbb{C}(\mathbb{S})\to \mathbb{C}(\mathbb{S}')$
such that
$\Box_R(A): \mathbb{C}(\mathbb{S})\to \mathbb{C}(\mathbb{S}')$
such that
![]() $\Box_R(A)\leq A$
in the lattice of monotonic maps with the pointwise order.
$\Box_R(A)\leq A$
in the lattice of monotonic maps with the pointwise order.
Scott continuity
We refer to Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003) for the definitions of Scott-continuous map, way-below relation
![]() $\ll$
, and continuous lattice. Restricting to compact metric spaces is mathematically appealing, since in this case a monotonic map
$\ll$
, and continuous lattice. Restricting to compact metric spaces is mathematically appealing, since in this case a monotonic map
![]() $A\,:\,\mathbb{C}(\mathbb{S})\to \mathbb{C}(\mathbb{S}')$
is robust exactly when it is Scott continuous, and the complete lattices
$A\,:\,\mathbb{C}(\mathbb{S})\to \mathbb{C}(\mathbb{S}')$
is robust exactly when it is Scott continuous, and the complete lattices
![]() $\mathbb{C}(\mathbb{S})$
and
$\mathbb{C}(\mathbb{S})$
and
![]() $\mathbb{C}(\mathbb{S}')$
are
$\mathbb{C}(\mathbb{S}')$
are
![]() $\omega$
-continuous (Moggi et al., Reference Moggi, Farjudian, Duracz and Taha2018).
$\omega$
-continuous (Moggi et al., Reference Moggi, Farjudian, Duracz and Taha2018).
A complete lattice X is
![]() $\omega$
-continuous when it has a countable base B, i.e., a countable subset of X such for every
$\omega$
-continuous when it has a countable base B, i.e., a countable subset of X such for every
![]() $x \in X$
, the subset
$x \in X$
, the subset
![]() $B_x\stackrel{\triangle}{=}\{b \in B \mid b\ll x\}$
is directed and
$B_x\stackrel{\triangle}{=}\{b \in B \mid b\ll x\}$
is directed and
![]() $x = \sup B_x$
. Moreover, by fixing an enumeration e of the base, one can define when an element
$x = \sup B_x$
. Moreover, by fixing an enumeration e of the base, one can define when an element
![]() $x \in X$
is computable, namely, when the set
$x \in X$
is computable, namely, when the set
![]() $\{n \in \mathbb{N} \mid e(n)\in B_x\}$
is a recursively enumerable subset of
$\{n \in \mathbb{N} \mid e(n)\in B_x\}$
is a recursively enumerable subset of
![]() $\mathbb{N}$
. The notion of computable can be extended to Scott-continuous maps between
$\mathbb{N}$
. The notion of computable can be extended to Scott-continuous maps between
![]() $\omega$
-continuous lattices because these maps, under the pointwise order, form an
$\omega$
-continuous lattices because these maps, under the pointwise order, form an
![]() $\omega$
-continuous lattice.
$\omega$
-continuous lattice.
Ideally, we would like to focus on computable analyses, but we settle for the broader class of Scott-continuous analyses, since they are better behaved. For instance, every monotonic map
![]() $A:X\to X'$
between complete lattices has a best (i.e., tightest) Scott-continuous approximation
$A:X\to X'$
between complete lattices has a best (i.e., tightest) Scott-continuous approximation
![]() $\Box_S(A):X\to X'$
, while there is no best computable approximation of a monotonic map between (effectively given)
$\Box_S(A):X\to X'$
, while there is no best computable approximation of a monotonic map between (effectively given)
![]() $\omega$
-continuous lattices.
$\omega$
-continuous lattices.
Related results
In Moggi et al. (Reference Moggi, Farjudian, Duracz and Taha2018), we defined robustness as a property of analyses, i.e., monotonic maps
![]() $A\,:\,\mathbb{C}(\mathbb{S}_1)\to \mathbb{C}(\mathbb{S}_2)$
, where
$A\,:\,\mathbb{C}(\mathbb{S}_1)\to \mathbb{C}(\mathbb{S}_2)$
, where
![]() $\mathbb{S}_i$
are metric spaces, and
$\mathbb{S}_i$
are metric spaces, and
![]() $\mathbb{C}(\mathbb{S}_i)$
are the complete lattices of closed subsets of
$\mathbb{C}(\mathbb{S}_i)$
are the complete lattices of closed subsets of
![]() $\mathbb{S}_i$
, ordered by reverse inclusion. In the same paper, we proved that:
$\mathbb{S}_i$
, ordered by reverse inclusion. In the same paper, we proved that:
-
Robustness of A amounts to continuity with respect to suitable
 $T_0$
-topologies
$T_0$
-topologies
 $\tau_R(\mathbb{S}_i)$
on the carrier sets of
$\tau_R(\mathbb{S}_i)$
on the carrier sets of
 $\mathbb{C}(\mathbb{S}_i)$
, called robust topologies (see Definition 2.25). In general, the topology
$\mathbb{C}(\mathbb{S}_i)$
, called robust topologies (see Definition 2.25). In general, the topology
 $\tau_R(\mathbb{S}_i)$
depends on the metric of
$\tau_R(\mathbb{S}_i)$
depends on the metric of
 $\mathbb{S}_i$
.
$\mathbb{S}_i$
. -
When
 $\mathbb{S}_i$
is compact, the topology
$\mathbb{S}_i$
is compact, the topology
 $\tau_R(\mathbb{S}_i)$
coincides with the Scott topology
$\tau_R(\mathbb{S}_i)$
coincides with the Scott topology
 $\tau_S(\mathbb{S}_i)$
on
$\tau_S(\mathbb{S}_i)$
on
 $\mathbb{C}(\mathbb{S}_i)$
. Thus, in this case,
$\mathbb{C}(\mathbb{S}_i)$
. Thus, in this case,
 $\tau_R(\mathbb{S}_i)$
depends only on the topology induced by the metric on
$\tau_R(\mathbb{S}_i)$
depends only on the topology induced by the metric on
 $\mathbb{S}_i$
.
$\mathbb{S}_i$
.
In particular, when both
![]() $\mathbb{S}_1$
and
$\mathbb{S}_1$
and
![]() $\mathbb{S}_2$
are compact, robustness and Scott continuity are equivalent properties of A, and the complete lattices
$\mathbb{S}_2$
are compact, robustness and Scott continuity are equivalent properties of A, and the complete lattices
![]() $\mathbb{C}(\mathbb{S}_i)$
are
$\mathbb{C}(\mathbb{S}_i)$
are
![]() $\omega$
-continuous. In Moggi et al. (Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019), we prove that every analysis
$\omega$
-continuous. In Moggi et al. (Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019), we prove that every analysis
![]() $A\,:\,\mathbb{C}(\mathbb{S}_1)\to \mathbb{C}(\mathbb{S}_2)$
has a best robust approximation
$A\,:\,\mathbb{C}(\mathbb{S}_1)\to \mathbb{C}(\mathbb{S}_2)$
has a best robust approximation
![]() $\Box_R(A)$
, when
$\Box_R(A)$
, when
![]() $\mathbb{S}_2$
is compact, with
$\mathbb{S}_2$
is compact, with
![]() $\Box_R(A)(C)$
given by
$\Box_R(A)(C)$
given by
![]() $\bigcap\{A(C_\delta) \mid \delta>0\}$
, where the closed subset
$\bigcap\{A(C_\delta) \mid \delta>0\}$
, where the closed subset
![]() $C_\delta\stackrel{\triangle}{=}\overline{B(C,\delta)}$
is called
$C_\delta\stackrel{\triangle}{=}\overline{B(C,\delta)}$
is called
![]() $\delta$
-fattening of C. When
$\delta$
-fattening of C. When
![]() $\mathbb{S}_1$
is not compact, however,
$\mathbb{S}_1$
is not compact, however,
![]() $\Box_R(A)$
may fail to be Scott continuous, and
$\Box_R(A)$
may fail to be Scott continuous, and
![]() $\mathbb{C}(\mathbb{S}_1)$
may fail to be
$\mathbb{C}(\mathbb{S}_1)$
may fail to be
![]() $\omega$
-continuous.
$\omega$
-continuous.
Motivating examples
Examples of metric spaces that are not compact are Banach Spaces. In applications, one usually considers closed bounded subsets of Banach spaces. In finite-dimensional Banach spaces, all closed bounded subsets are compact, but this fails in the infinite-dimensional case. To motivate the need to go beyond compact subsets, we present some examples of closed bounded subsets of infinite-dimensional Banach spaces that are not compact:
-
Probability distributions for a system with a countable set of states form a closed bounded subset of
 $\ell_1$
, i.e., the Banach space of sequences
$\ell_1$
, i.e., the Banach space of sequences
 $(x_n \mid n \in \omega)$
in
$(x_n \mid n \in \omega)$
in
 $\mathbb{R}^\omega$
such that
$\mathbb{R}^\omega$
such that
 $\sum_{n \in \omega}\lvert\thinspace {x_n} \thinspace\rvert$
is bounded. More generally, probability distributions on a measurable space
$\sum_{n \in \omega}\lvert\thinspace {x_n} \thinspace\rvert$
is bounded. More generally, probability distributions on a measurable space
 $(X,\Sigma)$
form a closed bounded subset of
$(X,\Sigma)$
form a closed bounded subset of
 $ca(\Sigma)$
, i.e., the Banach space of countably additive bounded signed measures on
$ca(\Sigma)$
, i.e., the Banach space of countably additive bounded signed measures on
 $\Sigma$
. This subset is not compact when the cardinality of
$\Sigma$
. This subset is not compact when the cardinality of
 $\Sigma$
is infinite.
$\Sigma$
is infinite. -
Continuous maps from a compact Hausdorff space X to a compact interval [a,b] in
 $\mathbb{R}$
form a closed bounded subset of C(X), i.e., the Banach space of continuous maps from X to
$\mathbb{R}$
form a closed bounded subset of C(X), i.e., the Banach space of continuous maps from X to
 $\mathbb{R}$
. For instance, these maps could represent the height as a function of the position.
$\mathbb{R}$
. For instance, these maps could represent the height as a function of the position. -
Closed bounded subsets of feature spaces arising from kernel methods in machine learning (Hofmann et al., Reference Hofmann, Schölkopf and Smola2008). Usually, feature spaces are Hilbert spaces, whose carrier sets consist of real-valued maps. All Hilbert spaces with a countable base are isomorphic to
 $\ell_2$
, i.e., the Hilbert space of sequences
$\ell_2$
, i.e., the Hilbert space of sequences
 $(x_n \mid n \in \omega)$
in
$(x_n \mid n \in \omega)$
in
 $\mathbb{R}^\omega$
such that
$\mathbb{R}^\omega$
such that
 $\sum_{n \in \omega}\lvert\thinspace {x_n^2} \thinspace\rvert$
is bounded.
$\sum_{n \in \omega}\lvert\thinspace {x_n^2} \thinspace\rvert$
is bounded. -
Closed bounded subsets of Sobolev spaces
 $W^{m,p}(\Omega)$
, in which
$W^{m,p}(\Omega)$
, in which
 $\Omega \subseteq \mathbb{R}^n$
is an open set. These sets commonly appear in solution of partial differential equations (Brezis, Reference Brezis2011).
$\Omega \subseteq \mathbb{R}^n$
is an open set. These sets commonly appear in solution of partial differential equations (Brezis, Reference Brezis2011).
Contribution
For simplicity, we consider analyses of the form
![]() $A\,:\,\mathbb{C}(\mathbb{S})\to \mathbb{C}(1)$
, with 1 denoting the one-point metric space, although the results hold also when 1 is replaced by a compact metric space, e.g., a compact interval [a,b] of the real line. The lattice
$A\,:\,\mathbb{C}(\mathbb{S})\to \mathbb{C}(1)$
, with 1 denoting the one-point metric space, although the results hold also when 1 is replaced by a compact metric space, e.g., a compact interval [a,b] of the real line. The lattice
![]() $\mathbb{C}(1)$
is (isomorphic to) the two-point lattice
$\mathbb{C}(1)$
is (isomorphic to) the two-point lattice
![]() $\Sigma$
and the complete lattice
$\Sigma$
and the complete lattice
![]() $\mathbb{C}(\mathbb{S})\to \Sigma$
is isomorphic to that of upward closed subsets of
$\mathbb{C}(\mathbb{S})\to \Sigma$
is isomorphic to that of upward closed subsets of
![]() $\mathbb{C}(\mathbb{S})$
, ordered by inclusion.
$\mathbb{C}(\mathbb{S})$
, ordered by inclusion.
This paper proposes a way to reconcile robustness and Scott continuity when
![]() $\mathbb{S}$
is not compact. The general idea is to construct an
$\mathbb{S}$
is not compact. The general idea is to construct an
![]() $\omega$
-continuous lattice D related to
$\omega$
-continuous lattice D related to
![]() $\mathbb{C}(\mathbb{S})$
by an adjunction:
$\mathbb{C}(\mathbb{S})$
by an adjunction:

such that the composite map
![]() $A'\circ \iota_*:\mathbb{C}(\mathbb{S})\to \Sigma$
is robust whenever the map
$A'\circ \iota_*:\mathbb{C}(\mathbb{S})\to \Sigma$
is robust whenever the map
![]() $A'\,:\,D\to \Sigma$
is Scott continuous. Therefore, given an analysis
$A'\,:\,D\to \Sigma$
is Scott continuous. Therefore, given an analysis
![]() $A\,:\,\mathbb{C}(\mathbb{S})\to \Sigma$
, we can take the best Scott-continuous approximation A’ of
$A\,:\,\mathbb{C}(\mathbb{S})\to \Sigma$
, we can take the best Scott-continuous approximation A’ of
![]() $A\circ \iota^*\,:\,D\to \Sigma$
—in fact, any Scott-continuous approximation will do—and the composite map
$A\circ \iota^*\,:\,D\to \Sigma$
—in fact, any Scott-continuous approximation will do—and the composite map
![]() $A'\circ \iota_*$
is guaranteed to be a robust approximation of A.
$A'\circ \iota_*$
is guaranteed to be a robust approximation of A.
The
![]() $\omega$
-continuous lattice D that we construct is of the form
$\omega$
-continuous lattice D that we construct is of the form
![]() $\mathbb{C}(\overline{\mathbb{S}})$
, where
$\mathbb{C}(\overline{\mathbb{S}})$
, where
![]() $\overline{\mathbb{S}}$
is a compact Hausdorff space given by the limit of an
$\overline{\mathbb{S}}$
is a compact Hausdorff space given by the limit of an
![]() $\omega^{op}$
-chain of compact metric spaces related to
$\omega^{op}$
-chain of compact metric spaces related to
![]() $\mathbb{S}$
(see Theorem 3.10), and the adjunction
$\mathbb{S}$
(see Theorem 3.10), and the adjunction
![]() $\iota_*\vdash \iota^*$
is determined by a continuous map
$\iota_*\vdash \iota^*$
is determined by a continuous map
![]() $\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
. Thus, by moving from
$\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
. Thus, by moving from
![]() $\mathbb{S}$
to
$\mathbb{S}$
to
![]() $\overline{\mathbb{S}}$
, we gain compactness by giving up the metric structure.
$\overline{\mathbb{S}}$
, we gain compactness by giving up the metric structure.
In general,
![]() $\overline{\mathbb{S}}$
is not uniquely determined by
$\overline{\mathbb{S}}$
is not uniquely determined by
![]() $\mathbb{S}$
, although Theorem 3.11 provides some criteria for choosing the
$\mathbb{S}$
, although Theorem 3.11 provides some criteria for choosing the
![]() $\omega^{op}$
-chain of compact metric spaces which determines
$\omega^{op}$
-chain of compact metric spaces which determines
![]() $\overline{\mathbb{S}}$
.
$\overline{\mathbb{S}}$
.
Summary
The rest of the paper is organized as follows:
-
Section 2 contains the mathematical preliminaries, where we fix notation and definitions. We will also present some basic results, usually without proofs, unless the results are not available in textbooks, in which case we provide proofs or pointers to other papers which include the relevant proofs. Most definitions are standard or taken from other papers. The only exception is the category
 $\mathbf{Top}_A$
of topological analyses (Definition 2.9).
$\mathbf{Top}_A$
of topological analyses (Definition 2.9). -
The main theoretical results are in Section 3. These include properties of idempotents and their splittings in a generic category
 $\mathbb{A}$
(e.g., Theorem 3.9) and the construction (Theorem 3.10) of a continuous map
$\mathbb{A}$
(e.g., Theorem 3.9) and the construction (Theorem 3.10) of a continuous map
 $\iota\,:\,\mathbb{S}\to\overline{\mathbb{S}}$
relating a metric space
$\iota\,:\,\mathbb{S}\to\overline{\mathbb{S}}$
relating a metric space
 $\mathbb{S}$
to a compact Hausdorff space
$\mathbb{S}$
to a compact Hausdorff space
 $\overline{\mathbb{S}}$
.
$\overline{\mathbb{S}}$
. -
In Section 4, we apply the results of Section 3 to several examples of
 $\mathbb{S}$
, which include finite-dimensional Banach spaces
$\mathbb{S}$
, which include finite-dimensional Banach spaces
 $\ell_{m,p}$
, infinite -dimensional Banach spaces
$\ell_{m,p}$
, infinite -dimensional Banach spaces
 $\ell_{p}$
(i.e., sequence spaces), and closed unit balls
$\ell_{p}$
(i.e., sequence spaces), and closed unit balls
 $B_{p}$
in sequence spaces.
$B_{p}$
in sequence spaces. -
In Section 5, we investigate loss of precision when moving from the complete lattice
 $\mathbb{C}(\mathbb{S})$
to the
$\mathbb{C}(\mathbb{S})$
to the
 $\omega$
-continuous lattice
$\omega$
-continuous lattice
 $\mathbb{C}(\overline{\mathbb{S}})$
, when
$\mathbb{C}(\overline{\mathbb{S}})$
, when
 $\mathbb{S}$
is a closed unit ball
$\mathbb{S}$
is a closed unit ball
 $B_{p}$
. In Theorem 5.4, we characterize the closed subsets of
$B_{p}$
. In Theorem 5.4, we characterize the closed subsets of
 $\ell_{p}$
(with
$\ell_{p}$
(with
 $1 < p < \infty$
) for which there is no loss of precision as those that can be expressed as a non-empty intersection of finite unions of closed balls.
$1 < p < \infty$
) for which there is no loss of precision as those that can be expressed as a non-empty intersection of finite unions of closed balls. -
We conclude the paper with some remarks and suggestions for future work in Section 6.
2. Mathematical Preliminaries
In this section, we present the basic technical background—including the notation—that will be used throughout the paper. We assume some familiarity with Category Theory, see Borceux (Reference Borceux1994). We use standard terminology for topological and metric spaces. At times, we may refer to a structure by its carrier set. For instance, for a metric space (X,d), we may simply write “the metric space X.” For brevity, in the text, we will henceforth use the word “carrier” instead of “carrier set.”
We use the “
![]() $\in$
” symbol to denote set membership (e.g.,
$\in$
” symbol to denote set membership (e.g.,
![]() $x \in X$
) and “
$x \in X$
) and “
![]() $:$
” symbol to denote function types (e.g.,
$:$
” symbol to denote function types (e.g.,
![]() $f: X \to Y$
) and also to denote objects and arrows in categories (e.g.,
$f: X \to Y$
) and also to denote objects and arrows in categories (e.g.,
![]() $A:\mathbf{Top}_0$
and
$A:\mathbf{Top}_0$
and
![]() $f:\mathbf{Top}_0(A,B)$
). A natural number is identified with the set of its predecessors, i.e.,
$f:\mathbf{Top}_0(A,B)$
). A natural number is identified with the set of its predecessors, i.e.,
![]() $0 = \emptyset$
and
$0 = \emptyset$
and
![]() $n = {{\left\{{0, \ldots, n-1}\right\}}}$
, for any
$n = {{\left\{{0, \ldots, n-1}\right\}}}$
, for any
![]() $n \geq 1$
. We write
$n \geq 1$
. We write
![]() $\mathbb{N}$
or
$\mathbb{N}$
or
![]() $\omega$
for the set of natural numbers. When the order matters
$\omega$
for the set of natural numbers. When the order matters
![]() $\omega$
denotes the set of natural numbers ordered by inclusion, while
$\omega$
denotes the set of natural numbers ordered by inclusion, while
![]() $\mathbb{N}$
denotes the set of natural numbers with the discrete order. We write
$\mathbb{N}$
denotes the set of natural numbers with the discrete order. We write
![]() $(x_n \mid n \in \omega)$
to denote a countable sequence, and when the indexing set is clear from the context, we just write
$(x_n \mid n \in \omega)$
to denote a countable sequence, and when the indexing set is clear from the context, we just write
![]() $(x_n\mid n)$
.
$(x_n\mid n)$
.
The powerset of a set X is denoted by
![]() $\mathsf{P}(X)$
,
$\mathsf{P}(X)$
,
![]() $\subseteq$
denotes subset inclusion, and
$\subseteq$
denotes subset inclusion, and
![]() $\subset$
denotes strict subset inclusion, i.e.,
$\subset$
denotes strict subset inclusion, i.e.,
![]() $A \subset B \iff A \subseteq B \wedge A \neq B$
. Similarly, the finite powerset (i.e., the set of finite subsets) of X is denoted by
$A \subset B \iff A \subseteq B \wedge A \neq B$
. Similarly, the finite powerset (i.e., the set of finite subsets) of X is denoted by
![]() $\mathsf{P}_f(X)$
, and
$\mathsf{P}_f(X)$
, and
![]() $A\subseteq_f B$
denotes that A is a finite subset of B. When X is a topological space, we write
$A\subseteq_f B$
denotes that A is a finite subset of B. When X is a topological space, we write
![]() $\mathsf{O}(X)$
and
$\mathsf{O}(X)$
and
![]() $\mathsf{C}(X)$
for the subsets of
$\mathsf{C}(X)$
for the subsets of
![]() $\mathsf{P}(X)$
consisting of the open subsets and the closed subsets of X, respectively.
$\mathsf{P}(X)$
consisting of the open subsets and the closed subsets of X, respectively.
2.1. Categories of spaces
The spaces of interest for this paper are (extended) metric spaces1 and Hausdorff spaces. However, in examples we restrict to Banach spaces, and some constructions extend to arbitrary topological spaces. Figure 1 summarizes the relations among the following categories of spaces.

Figure 1. Categories of spaces.
Definition 2.1 (Categories of Spaces)
-
 $\mathbf{Top}_0$
is the category of
$\mathbf{Top}_0$
is the category of
 $T_0$
-topological spaces
$T_0$
-topological spaces
 $(X,\tau)$
and continuous maps.
$(X,\tau)$
and continuous maps.
 $\mathbf{Haus}$
and
$\mathbf{Haus}$
and
 $\mathbf{KH}$
are the full sub-categories consisting of Hausdorff spaces (aka
$\mathbf{KH}$
are the full sub-categories consisting of Hausdorff spaces (aka
 $T_2$
-spaces) and compact Hausdorff spaces, respectively.
$T_2$
-spaces) and compact Hausdorff spaces, respectively. -
 $\mathbf{Met}$
is the category of extended metric spaces (X,d), i.e., the metric d can be
$\mathbf{Met}$
is the category of extended metric spaces (X,d), i.e., the metric d can be
 $\infty$
, and short maps, i.e., maps
$\infty$
, and short maps, i.e., maps
 $f: X_1 \to X_2$
such that
$f: X_1 \to X_2$
such that
 $d_2(f(x),f(x'))\leq d_1(x,x')$
for
$d_2(f(x),f(x'))\leq d_1(x,x')$
for
 $x,x' \in X_1$
. There are other maps one can consider between (extended) metric spaces, in particular isometries, i.e., metric preserving maps. The forgetful functor
$x,x' \in X_1$
. There are other maps one can consider between (extended) metric spaces, in particular isometries, i.e., metric preserving maps. The forgetful functor
 $U:\mathbf{Met} \to \mathbf{Haus}$
maps a metric d on X to the
$U:\mathbf{Met} \to \mathbf{Haus}$
maps a metric d on X to the
 $T_2$
-topology
$T_2$
-topology
 $\tau_d$
on X generated by the open balls.
$\tau_d$
on X generated by the open balls.
 $\mathbf{CMS}$
and
$\mathbf{CMS}$
and
 $\mathbf{KMS}$
are the full sub-categories of
$\mathbf{KMS}$
are the full sub-categories of
 $\mathbf{Met}$
consisting of Cauchy complete extended metric spaces and compact extended metric spaces, respectively. The objects in
$\mathbf{Met}$
consisting of Cauchy complete extended metric spaces and compact extended metric spaces, respectively. The objects in
 $\mathbf{KMS}$
are exactly the extended metric spaces whose underlying topological spaces are compact.
$\mathbf{KMS}$
are exactly the extended metric spaces whose underlying topological spaces are compact. -
 $\mathbf{NVS}$
is the category of normed vector spaces
$\mathbf{NVS}$
is the category of normed vector spaces
 $(X,\cdot,+,{{{\lVert\thinspace {-}\thinspace\rVert}}})$
and short linear maps. The forgetful functor
$(X,\cdot,+,{{{\lVert\thinspace {-}\thinspace\rVert}}})$
and short linear maps. The forgetful functor
 $U:\mathbf{NVS} \to \mathbf{Met}$
maps a normed vector space to the metric space with (the same carrier and) metric
$U:\mathbf{NVS} \to \mathbf{Met}$
maps a normed vector space to the metric space with (the same carrier and) metric
 $d(x',x)\stackrel{\triangle}{=}{{{\lVert\thinspace {x'-x}\thinspace\rVert}}}$
.
$d(x',x)\stackrel{\triangle}{=}{{{\lVert\thinspace {x'-x}\thinspace\rVert}}}$
.
 $\mathbf{Ban}$
is the full sub-category of
$\mathbf{Ban}$
is the full sub-category of
 $\mathbf{NVS}$
consisting of Banach spaces. The objects in
$\mathbf{NVS}$
consisting of Banach spaces. The objects in
 $\mathbf{Ban}$
are exactly the normed vector spaces whose underlying metric spaces are complete.
$\mathbf{Ban}$
are exactly the normed vector spaces whose underlying metric spaces are complete.
Example 2.2. As a running example, we consider the one-dimensional Banach space
![]() $\mathbb{R}:Ban$
. As a (complete) metric space
$\mathbb{R}:Ban$
. As a (complete) metric space
![]() $\mathbb{R}:\mathbf{CMS}$
, its metric is
$\mathbb{R}:\mathbf{CMS}$
, its metric is
![]() $d(x,y) \stackrel{\triangle}{=} \lvert\thinspace {x-y} \thinspace\rvert$
, while as a Hausdorff space
$d(x,y) \stackrel{\triangle}{=} \lvert\thinspace {x-y} \thinspace\rvert$
, while as a Hausdorff space
![]() $\mathbb{R}:\mathbf{Haus}$
, its topology
$\mathbb{R}:\mathbf{Haus}$
, its topology
![]() $\mathsf{O}(\mathbb{R})$
is the set of (Euclidean) open subsets of
$\mathsf{O}(\mathbb{R})$
is the set of (Euclidean) open subsets of
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
Recall that,
![]() $K:\mathbf{KH}$
is said to be a compactification of
$K:\mathbf{KH}$
is said to be a compactification of
![]() $X:\mathbf{Haus}$
, if X can be regarded as a dense sub-space (via a topological embedding) of K. There are several compactifications of
$X:\mathbf{Haus}$
, if X can be regarded as a dense sub-space (via a topological embedding) of K. There are several compactifications of
![]() $\mathbb{R}$
, for example:
$\mathbb{R}$
, for example:
-
The one-point (aka Alexandroff) compactification
 $\mathbb{R}_\infty$
with the carrier
$\mathbb{R}_\infty$
with the carrier
 $\mathbb{R} \cup {{\left\{{\infty}\right\}}}$
, whose open subsets are either in
$\mathbb{R} \cup {{\left\{{\infty}\right\}}}$
, whose open subsets are either in
 $\mathsf{O}(\mathbb{R})$
or subsets in
$\mathsf{O}(\mathbb{R})$
or subsets in
 $\mathsf{P}(\mathbb{R}_\infty)$
of the form
$\mathsf{P}(\mathbb{R}_\infty)$
of the form
 $A \cup {{\left\{{\infty}\right\}}}$
, where
$A \cup {{\left\{{\infty}\right\}}}$
, where
 $A\in\mathsf{O}(\mathbb{R})$
and its complement
$A\in\mathsf{O}(\mathbb{R})$
and its complement
 $A^c$
in
$A^c$
in
 $\mathbb{R}$
is compact.
$\mathbb{R}$
is compact. -
The two-point compactification
 $\overline{\mathbb{R}}$
, which is topologically homeomorphic to the interval [0,1] with the Euclidean topology. The two-point compactification of
$\overline{\mathbb{R}}$
, which is topologically homeomorphic to the interval [0,1] with the Euclidean topology. The two-point compactification of
 $\mathbb{R}$
has
$\mathbb{R}$
has
 $\mathbb{R} \cup {{\left\{{ -\infty, +\infty}\right\}}}$
as its carrier, with the order on
$\mathbb{R} \cup {{\left\{{ -\infty, +\infty}\right\}}}$
as its carrier, with the order on
 $\mathbb{R}$
extended so that
$\mathbb{R}$
extended so that
 $\forall x \in \mathbb{R}.\ -\infty < x < +\infty$
. The collection of sets of the form
$\forall x \in \mathbb{R}.\ -\infty < x < +\infty$
. The collection of sets of the form
 $[-\infty,x)$
, (x,y),
$[-\infty,x)$
, (x,y),
 $(y,+\infty]$
, with
$(y,+\infty]$
, with
 $x,y \in \mathbb{R}$
, forms a base for the two-point compactification.
$x,y \in \mathbb{R}$
, forms a base for the two-point compactification. -
The Stone-Čech compactification
 $\beta\mathbb{R}$
, which is characterized by the universal property that any continuous function from
$\beta\mathbb{R}$
, which is characterized by the universal property that any continuous function from
 $\mathbb{R}$
to a compact Hausdorff space K can be extended to a continuous function from
$\mathbb{R}$
to a compact Hausdorff space K can be extended to a continuous function from
 $\beta \mathbb{R}$
to K in a unique way. For more details see, e.g., Munkres (Reference Munkres2000, Chapter 5).
$\beta \mathbb{R}$
to K in a unique way. For more details see, e.g., Munkres (Reference Munkres2000, Chapter 5).
All three methods of compactification exemplified above have limitations. The two-point compactification may work only for topological spaces induced by a linear order. The one-point compactification works only for locally compact spaces, which do not include infinite-dimensional Banach spaces. The Stone-Čech compactification works for all Tychonoff spaces. The problem is that, even for simple spaces such as
![]() $\mathbb{R}$
, there is no concrete description of
$\mathbb{R}$
, there is no concrete description of
![]() $\beta\mathbb{R}$
, which makes it impossible to be used in an effective framework as we intend to do.
$\beta\mathbb{R}$
, which makes it impossible to be used in an effective framework as we intend to do.
The following theorems recall some properties of categories and functors in Figure 1.
Theorem 2.3. The categories in the following diagram have finite limits and finite sums, and the functors preserve them:
The categories
![]() $\mathbf{CMS}$
,
$\mathbf{CMS}$
,
![]() $\mathbf{Met,}$
and
$\mathbf{Met,}$
and
![]() $\mathbf{Haus}$
have also small limits and small colimits.
$\mathbf{Haus}$
have also small limits and small colimits.
For the existence of sums and infinitary products, it is essential to use extended metric spaces.
Theorem 2.4. The categories in the following diagram have small limits and finite sums, and the functors preserve them:
The categories have also small colimits.
Definition 2.5. (Imprecision and Fattening) Given a metric space
![]() $\mathbb{S}$
, with metric d, we define:
$\mathbb{S}$
, with metric d, we define:
-
(1)
 $B(S,\delta)\stackrel{\triangle}{=}\{y \mid \exists x \in S.d(x,y)<\delta\} \in \mathsf{O}(\mathbb{S})$
, where
$B(S,\delta)\stackrel{\triangle}{=}\{y \mid \exists x \in S.d(x,y)<\delta\} \in \mathsf{O}(\mathbb{S})$
, where
 $S \in \mathsf{P}(\mathbb{S})$
and
$S \in \mathsf{P}(\mathbb{S})$
and
 $\delta>0$
. The subset
$\delta>0$
. The subset
 $B(S,\delta)$
is open, because it is the union of the open balls
$B(S,\delta)$
is open, because it is the union of the open balls
 $B(x,\delta)\stackrel{\triangle}{=}\{y \mid d(x,y)<\delta\}$
with
$B(x,\delta)\stackrel{\triangle}{=}\{y \mid d(x,y)<\delta\}$
with
 $x \in S$
.
$x \in S$
. -
(2) the closure
 $\overline{S} \in \mathsf{C}(\mathbb{S})$
of
$\overline{S} \in \mathsf{C}(\mathbb{S})$
of
 $S \in \mathsf{P}(\mathbb{S})$
, i.e., the smallest
$S \in \mathsf{P}(\mathbb{S})$
, i.e., the smallest
 $C \in \mathsf{C}(\mathbb{S})$
such that
$C \in \mathsf{C}(\mathbb{S})$
such that
 $S\subseteq C$
.
$S\subseteq C$
. -
(3)
 is the
is the
 $\delta$
-fattening of
$\delta$
-fattening of
 $S \in \mathsf{P}(\mathbb{S})$
.
$S \in \mathsf{P}(\mathbb{S})$
.
While
![]() $S_\delta$
is always closed, the subset
$S_\delta$
is always closed, the subset
![]() $C(S,\delta)\stackrel{\triangle}{=}\{y \mid \exists x \in S.d(x,y)\leq\delta\}$
may fail to be closed, e.g., in the metric space
$C(S,\delta)\stackrel{\triangle}{=}\{y \mid \exists x \in S.d(x,y)\leq\delta\}$
may fail to be closed, e.g., in the metric space
![]() $\mathbb{R}$
we have
$\mathbb{R}$
we have
![]() $B(S,1)=C(S,1)=(-2,2)\subset [-2,2]=S_1$
, when S is the open interval
$B(S,1)=C(S,1)=(-2,2)\subset [-2,2]=S_1$
, when S is the open interval
![]() $(-1,1)$
. Moreover, when
$(-1,1)$
. Moreover, when
![]() $C(S,\delta)$
is closed it may fail to coincide with
$C(S,\delta)$
is closed it may fail to coincide with
![]() $S_\delta$
, e.g., in a 1-discrete metric space
$S_\delta$
, e.g., in a 1-discrete metric space
![]() $\mathbb{S}$
(i.e., the metric is either 0 or 1), we have
$\mathbb{S}$
(i.e., the metric is either 0 or 1), we have
![]() $B(S,1)=S_1=S\subset\mathbb{S}=C(S,1)$
, for any proper non-empty subset S of
$B(S,1)=S_1=S\subset\mathbb{S}=C(S,1)$
, for any proper non-empty subset S of
![]() $\mathbb{S}$
. We summarize some basic properties of
$\mathbb{S}$
. We summarize some basic properties of
![]() $B(S,\delta)$
and
$B(S,\delta)$
and
![]() $S_\delta$
, see also Moggi et al. (Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019).
$S_\delta$
, see also Moggi et al. (Reference Moggi, Farjudian, Taha, Cherubini, Sabadini and Tini2019).
Proposition 2.6.
In a metric space
![]() $\mathbb{S,}$
the following claims hold for any
$\mathbb{S,}$
the following claims hold for any
![]() $S \in \mathsf{P}(\mathbb{S})$
and
$S \in \mathsf{P}(\mathbb{S})$
and
![]() $\delta,\delta'>0$
.
$\delta,\delta'>0$
.
-
(1)
 $B(B(S,\delta),\delta')\subseteq B(S,\delta+\delta')$
.
$B(B(S,\delta),\delta')\subseteq B(S,\delta+\delta')$
. -
(2)

-
(3)

-
(4)

We now prove two properties of short maps (between metric spaces) and compact metric spaces expressed in terms of
![]() $\delta$
-fattening. These properties are relevant to the proof of Theorem 3.10.
$\delta$
-fattening. These properties are relevant to the proof of Theorem 3.10.
Proposition 2.7.
If
![]() $f:\mathbf{Met}(\mathbb{S},\mathbb{S}')$
, then the following claims hold for any
$f:\mathbf{Met}(\mathbb{S},\mathbb{S}')$
, then the following claims hold for any
![]() $S \in \mathsf{P}(\mathbb{S})$
and
$S \in \mathsf{P}(\mathbb{S})$
and
![]() $\delta>0$
.
$\delta>0$
.
-
(1)
 $f(B(S,\delta))\subseteq B(f(S),\delta)$
.
$f(B(S,\delta))\subseteq B(f(S),\delta)$
. -
(2)
 $\overline{f(S_\delta)}\subseteq f(S)_\delta$
.
$\overline{f(S_\delta)}\subseteq f(S)_\delta$
.
Proof. For (1) observe that
![]() $y' \in f(B(S,\delta))$
means
$y' \in f(B(S,\delta))$
means
![]() $\exists y \in B(S,\delta).y'=f(y)$
, i.e.,
$\exists y \in B(S,\delta).y'=f(y)$
, i.e.,
![]() $\exists y.\exists x \in S.y'=f(y)\land d(y,x)<\delta$
. Thus,
$\exists y.\exists x \in S.y'=f(y)\land d(y,x)<\delta$
. Thus,
![]() $\exists x \in S.d'(y',f(x))<\delta$
, because
$\exists x \in S.d'(y',f(x))<\delta$
, because
![]() $d'(y',f(x))=d'(f(y),f(x))\leq d(y,x)<\delta$
(by f short), i.e.,
$d'(y',f(x))=d'(f(y),f(x))\leq d(y,x)<\delta$
(by f short), i.e.,
![]() $y' \in B(f(S),\delta)$
.
$y' \in B(f(S),\delta)$
.
Claim (2) follows from (1) and the chain of equivalences
![]() $f(A)\subseteq C'\iff A\subseteq f^{-1}(C')\iff \overline{f(\overline{A})}\subseteq C'$
, which holds for any
$f(A)\subseteq C'\iff A\subseteq f^{-1}(C')\iff \overline{f(\overline{A})}\subseteq C'$
, which holds for any
![]() $f:\mathbf{Haus}(\mathbb{S},\mathbb{S}')$
,
$f:\mathbf{Haus}(\mathbb{S},\mathbb{S}')$
,
![]() $A \in \mathsf{P}(\mathbb{S})$
and
$A \in \mathsf{P}(\mathbb{S})$
and
![]() $C' \in \mathsf{C}(\mathbb{S}')$
. Namely, take
$C' \in \mathsf{C}(\mathbb{S}')$
. Namely, take
![]() $A=B(S,\delta)$
and
$A=B(S,\delta)$
and
![]() $C'=f(S)_\delta$
.
$C'=f(S)_\delta$
.
Proposition 2.8.
If
![]() $\mathbb{S}:\mathbf{KMS}$
, then
$\mathbb{S}:\mathbf{KMS}$
, then
![]() $\forall K \in \mathsf{C}(\mathbb{S}).\forall O \in \mathsf{O}(\mathbb{S}). K\subseteq O\implies\exists\delta>0.K_\delta\subseteq O$
.
$\forall K \in \mathsf{C}(\mathbb{S}).\forall O \in \mathsf{O}(\mathbb{S}). K\subseteq O\implies\exists\delta>0.K_\delta\subseteq O$
.
Proof. First, in a compact metric space closed subsets are compact, thus
![]() $K \in \mathsf{C}(\mathbb{S})$
and
$K \in \mathsf{C}(\mathbb{S})$
and
![]() $K_\delta$
are compact. If the claim were false, then there exist
$K_\delta$
are compact. If the claim were false, then there exist
![]() $K \in \mathsf{C}(\mathbb{S})$
and
$K \in \mathsf{C}(\mathbb{S})$
and
![]() $O \in \mathsf{O}(\mathbb{S})$
such that
$O \in \mathsf{O}(\mathbb{S})$
such that
![]() $K\subseteq O$
and
$K\subseteq O$
and
![]() $\forall n.\exists x_n \in K_{\delta_n}.x_n\not\in O$
, where
$\forall n.\exists x_n \in K_{\delta_n}.x_n\not\in O$
, where
![]() $\delta_n\stackrel{\triangle}{=} 2^{-n}$
. Since the sequence
$\delta_n\stackrel{\triangle}{=} 2^{-n}$
. Since the sequence
![]() $(x_n \mid n)$
is in the compact subset
$(x_n \mid n)$
is in the compact subset
![]() $K_{\delta_0}$
, it must have an accumulation point x.
$K_{\delta_0}$
, it must have an accumulation point x.
For simplicity, we assume that
![]() $(x_n \mid n)$
is a Cauchy sequence and x is its limit. Since the Cauchy sequence
$(x_n \mid n)$
is a Cauchy sequence and x is its limit. Since the Cauchy sequence
![]() $(x_n \mid n)$
is eventually in
$(x_n \mid n)$
is eventually in
![]() $K_\delta$
for any
$K_\delta$
for any
![]() $\delta>0$
, we conclude that
$\delta>0$
, we conclude that
![]() $x\in K$
, and also
$x\in K$
, and also
![]() $x\in O$
. Since O is open, there exists an open ball
$x\in O$
. Since O is open, there exists an open ball
![]() $B(x,\delta)\subseteq O$
, which contradicts the assumption
$B(x,\delta)\subseteq O$
, which contradicts the assumption
![]() $\forall n.x_n\not\in O$
.
$\forall n.x_n\not\in O$
.
2.2 Categories of analyses
We define an analysis as a monotonic map between complete lattices. However, we need to consider further properties of analyses, that (with the exception of computability) can be defined as continuity with respect to suitable topologies on (the carrier of) complete lattices. For this reason, we introduce the category
![]() $\mathbf{Top}_A$
of topological analyses, which refines the category
$\mathbf{Top}_A$
of topological analyses, which refines the category
![]() $\mathbf{Po}_A$
of analyses (see Figure 2).
$\mathbf{Po}_A$
of analyses (see Figure 2).

Figure 2. Poset-enriched categories.
Definition 2.9. (Category of Analyses)
-
 $\mathbf{Po}$
is the category of posets and monotonic maps.
$\mathbf{Po}$
is the category of posets and monotonic maps. -
The forgetful functor
 $U: \mathbf{Top}_0 \to \mathbf{Po}$
maps a
$U: \mathbf{Top}_0 \to \mathbf{Po}$
maps a
 $T_0$
-topology
$T_0$
-topology
 $\tau$
on X to the specialization order
$\tau$
on X to the specialization order
 $\leq_\tau$
on X, i.e.,
$\leq_\tau$
on X, i.e.,
 $x\leq_\tau y\stackrel{\triangle}{\iff}\forall O \in \tau. (x\in O\implies y\in O$
).
$x\leq_\tau y\stackrel{\triangle}{\iff}\forall O \in \tau. (x\in O\implies y\in O$
). -
The inclusion functor
-

-
maps a poset
 $\leq$
on X to the Alexandroff topology
$\leq$
on X to the Alexandroff topology
 $\tau_\leq$
of the upward closed subsets of X, i.e.,
$\tau_\leq$
of the upward closed subsets of X, i.e.,
 $O\in\tau_\leq\stackrel{\triangle}{\iff}\forall x,y \in X.x\in O\land x\leq y\implies y\in O$
.
$O\in\tau_\leq\stackrel{\triangle}{\iff}\forall x,y \in X.x\in O\land x\leq y\implies y\in O$
. -
 $\mathbf{Po}_A$
, the category of analyses, is the full sub-category of
$\mathbf{Po}_A$
, the category of analyses, is the full sub-category of
 $\mathbf{Po}$
consisting of complete lattices.
$\mathbf{Po}$
consisting of complete lattices. -
 $\mathbf{Top}_A$
, the category of topological analyses, is the full sub-category of
$\mathbf{Top}_A$
, the category of topological analyses, is the full sub-category of
 $\mathbf{Top}_0$
consisting of
$\mathbf{Top}_0$
consisting of
 $T_0$
-spaces whose specialization order is a complete lattice.
$T_0$
-spaces whose specialization order is a complete lattice.
Theorem 2.10. The following statements hold:
-
(1) The categories
 $\mathbf{Po}$
and
$\mathbf{Po}$
and
 $\mathbf{Top}_0$
are
$\mathbf{Top}_0$
are
 $\mathbf{Po}$
-enriched and have small limits and small colimits.
$\mathbf{Po}$
-enriched and have small limits and small colimits. -
(2) The functors U and A are
 $\mathbf{Po}$
-enriched, and A is left adjoint to U.
$\mathbf{Po}$
-enriched, and A is left adjoint to U.
-
(3) The functor U preserves small limits and small sums.
-
(4) The functor A preserves finite limits and small colimits.
Proof. The
![]() $\mathbf{Po}$
-enrichment of
$\mathbf{Po}$
-enrichment of
![]() $\mathbf{Po}$
is given by its cartesian closed structure. Since U is faithful,
$\mathbf{Po}$
is given by its cartesian closed structure. Since U is faithful,
![]() $\mathbf{Top}_0(X,Y)$
is a subset of
$\mathbf{Top}_0(X,Y)$
is a subset of
![]() $\mathbf{Po}(UX,UY)$
and inherits the
$\mathbf{Po}(UX,UY)$
and inherits the
![]() $\mathbf{Po}$
-enrichment. It is easy to prove that
$\mathbf{Po}$
-enrichment. It is easy to prove that
![]() $\mathbf{Top}_0(AX,Y)=\mathbf{Po}(X,UY)$
. Thus, A is left adjoint to U also as
$\mathbf{Top}_0(AX,Y)=\mathbf{Po}(X,UY)$
. Thus, A is left adjoint to U also as
![]() $\mathbf{Po}$
-enriched functors.
$\mathbf{Po}$
-enriched functors.
Corollary 2.11 The following statements hold:
-
(1) The category
 $\mathbf{Po}_A$
is
$\mathbf{Po}_A$
is
 $\mathbf{Po}_A$
-enriched and has small products.
$\mathbf{Po}_A$
-enriched and has small products. -
(2) The category
 $\mathbf{Top}_A$
is
$\mathbf{Top}_A$
is
 $\mathbf{Po}$
-enriched and has small products.
$\mathbf{Po}$
-enriched and has small products.
-
(3) The
 $\mathbf{Po}$
-enriched functors U and A restrict to functors between
$\mathbf{Po}$
-enriched functors U and A restrict to functors between
 $\mathbf{Top}_A$
and
$\mathbf{Top}_A$
and
 $\mathbf{Po}_A$
.
$\mathbf{Po}_A$
.
Proof. The
![]() $\mathbf{Po}_A$
-enrichment of
$\mathbf{Po}_A$
-enrichment of
![]() $\mathbf{Po}_A$
is given by its cartesian closed structure. The other claims are easy consequences of Theorem 2.10 and the definition of
$\mathbf{Po}_A$
is given by its cartesian closed structure. The other claims are easy consequences of Theorem 2.10 and the definition of
![]() $\mathbf{Top}_A$
.
$\mathbf{Top}_A$
.
Theorem 2.12. (Topologies on a poset) Given a partial order
![]() $\leq$
on X, the set of
$\leq$
on X, the set of
![]() $T_0$
-topologies on X with specialization order
$T_0$
-topologies on X with specialization order
![]() $\leq$
ordered by reverse inclusion is a complete lattice
$\leq$
ordered by reverse inclusion is a complete lattice
![]() $\mathbf{Top}(\leq)$
, where:
$\mathbf{Top}(\leq)$
, where:
-
the least element
 $\tau_\bot$
is the Alexandroff topology
$\tau_\bot$
is the Alexandroff topology
 $\tau_\leq$
$\tau_\leq$
-
the top element
 $\tau_\top$
is the topology generated by the set
$\tau_\top$
is the topology generated by the set
 ${{\{{\not\downarrow y} \mid{y \in X}\}}}$
, where
${{\{{\not\downarrow y} \mid{y \in X}\}}}$
, where
 $\not\downarrow y\stackrel{\triangle}{=}\{x \in X \mid$
$\not\downarrow y\stackrel{\triangle}{=}\{x \in X \mid$
 $x\not\leq y\}$
$x\not\leq y\}$
-
the non-empty sups are given by intersection.
Moreover, when X is finite
![]() $\mathbf{Top}(\leq)$
is trivial, i.e.,
$\mathbf{Top}(\leq)$
is trivial, i.e.,
![]() $\tau_\bot=\tau_\top$
.
$\tau_\bot=\tau_\top$
.
Proof. It is easy to show that
![]() $(X,\tau_\top)$
and
$(X,\tau_\top)$
and
![]() $(X,\tau_\bot)$
are
$(X,\tau_\bot)$
are
![]() $T_0$
-spaces with specialization order
$T_0$
-spaces with specialization order
![]() $\leq$
. Given a
$\leq$
. Given a
![]() $T_0$
-topology
$T_0$
-topology
![]() $\tau$
on X with specialization order
$\tau$
on X with specialization order
![]() $\leq$
we have
$\leq$
we have
![]() $\tau_\top\subseteq\tau\subseteq\tau_\bot$
, because:
$\tau_\top\subseteq\tau\subseteq\tau_\bot$
, because:
-
each
 $O \in \tau$
is upward closed, by definition of
$O \in \tau$
is upward closed, by definition of
 $\leq_\tau$
,
$\leq_\tau$
, -
each
 $\not\downarrow y$
is in
$\not\downarrow y$
is in
 $\tau$
, because
$\tau$
, because
 $\not\downarrow y=\bigcup\{O \in \tau \mid y\not\in O\}$
.
$\not\downarrow y=\bigcup\{O \in \tau \mid y\not\in O\}$
.
Therefore,
![]() $\tau_\top$
and
$\tau_\top$
and
![]() $\tau_\bot$
are respectively the top and bottom element in
$\tau_\bot$
are respectively the top and bottom element in
![]() $\mathbf{Top}(\leq)$
. Since the topologies on a set X (ordered by reverse inclusion) form a complete lattice, with (non-empty) sups given by intersections, so do the topologies
$\mathbf{Top}(\leq)$
. Since the topologies on a set X (ordered by reverse inclusion) form a complete lattice, with (non-empty) sups given by intersections, so do the topologies
![]() $\tau$
on X such that
$\tau$
on X such that
![]() $\tau_\top\subseteq\tau\subseteq\tau_\bot$
. Moreover, such topologies are
$\tau_\top\subseteq\tau\subseteq\tau_\bot$
. Moreover, such topologies are
![]() $T_0$
, because
$T_0$
, because
![]() $\tau_\top$
is.
$\tau_\top$
is.
For every
![]() $x \in X,$
we have
$x \in X,$
we have
![]() $\uparrow x=\bigcap\{\not\downarrow y \mid y \in X\land x\not\leq y\}$
. When X is finite, the right-hand side of the equality is a finite intersection of open sets in
$\uparrow x=\bigcap\{\not\downarrow y \mid y \in X\land x\not\leq y\}$
. When X is finite, the right-hand side of the equality is a finite intersection of open sets in
![]() $\tau_\top$
, thus
$\tau_\top$
, thus
![]() $\uparrow x\in\tau_\top$
, and therefore,
$\uparrow x\in\tau_\top$
, and therefore,
![]() $\tau_\bot\subseteq\tau_\top$
.
$\tau_\bot\subseteq\tau_\top$
.
When
![]() $\leq$
is an object in
$\leq$
is an object in
![]() $\mathbf{Po}_A$
, the topologies in
$\mathbf{Po}_A$
, the topologies in
![]() $\mathbf{Top}(\leq)$
are objects in
$\mathbf{Top}(\leq)$
are objects in
![]() $\mathbf{Top}_A$
.
$\mathbf{Top}_A$
.
2.3 Adjunctions and best approximations
A key property of categories of analyses is poset-enrichment, which provides a qualitative criterion for comparing analyses, and allows the definition of adjunctions between two complete lattices.
Definition 2.13. (Adjunction) An adjunction in a
![]() $\mathbf{Po}$
-enriched category
$\mathbf{Po}$
-enriched category
![]() $\mathbb{A}$
, notation
$\mathbb{A}$
, notation
![]() $f\dashv g$
, is a pair of maps
$f\dashv g$
, is a pair of maps
![]() in
in
![]() $\mathbb{A}$
such that
$\mathbb{A}$
such that
![]() $f\circ g\leq\text{id}_Y$
and
$f\circ g\leq\text{id}_Y$
and
![]() $g\circ f\geq\text{id}_X$
. The maps f and g are called left and right adjoint, respectively, and any one of these two maps uniquely determines the other.
$g\circ f\geq\text{id}_X$
. The maps f and g are called left and right adjoint, respectively, and any one of these two maps uniquely determines the other.
Remark 2.14. A characterization of adjunctions in
![]() $\mathbf{Po}$
is
$\mathbf{Po}$
is
![]() $f\dashv g$
iff
$f\dashv g$
iff
![]() $\forall x \in X. \forall y \in Y. (x\leq_X g(y)\iff f(x)\leq_Y y)$
. This characterization implies that in
$\forall x \in X. \forall y \in Y. (x\leq_X g(y)\iff f(x)\leq_Y y)$
. This characterization implies that in
![]() $\mathbf{Po}$
left adjoints preserve sups and (dually) right adjoints preserve infs.
$\mathbf{Po}$
left adjoints preserve sups and (dually) right adjoints preserve infs.
Theorem 2.15.
The
![]() $\mathbf{Po}$
-enriched categories
$\mathbf{Po}$
-enriched categories
![]() $\mathbf{Po}_A$
and
$\mathbf{Po}_A$
and
![]() $\mathbf{Top}_A$
have limits of
$\mathbf{Top}_A$
have limits of
![]() $\omega^{op}$
-chains of right adjoints.
$\omega^{op}$
-chains of right adjoints.
Proof. First, we prove the property for
![]() $\mathbf{Po}_A$
. Given an
$\mathbf{Po}_A$
. Given an
![]() $\omega^{op}$
-chain
$\omega^{op}$
-chain
![]() $(p_n:D_{n+1}\to D_n \mid n)$
of right adjoints in
$(p_n:D_{n+1}\to D_n \mid n)$
of right adjoints in
![]() $\mathbf{Po}_A$
, its limit in
$\mathbf{Po}_A$
, its limit in
![]() $\mathbf{Po}$
is the subset of
$\mathbf{Po}$
is the subset of
![]() $\prod_{n}\lvert\thinspace {D_n} \thinspace\rvert$
given by
$\prod_{n}\lvert\thinspace {D_n} \thinspace\rvert$
given by
![]() $\lvert\thinspace {D} \thinspace\rvert\stackrel{\triangle}{=}\{d \mid \forall n.d_n=p_n(d_{n+1})\}$
with the pointwise order
$\lvert\thinspace {D} \thinspace\rvert\stackrel{\triangle}{=}\{d \mid \forall n.d_n=p_n(d_{n+1})\}$
with the pointwise order
![]() $\leq_D$
. Right adjoints preserve infs; thus, infs in D exist and are computed pointwise. Therefore,
$\leq_D$
. Right adjoints preserve infs; thus, infs in D exist and are computed pointwise. Therefore,
![]() $D:\mathbf{Po}_A$
and the maps
$D:\mathbf{Po}_A$
and the maps
![]() $\pi_n:D \to D_n$
with
$\pi_n:D \to D_n$
with
![]() $\pi_n(d)=d_n$
form a limit cone (and preserve infs).
$\pi_n(d)=d_n$
form a limit cone (and preserve infs).
Given an
![]() $\omega^{op}$
-chain
$\omega^{op}$
-chain
![]() $(p_n:D_{n+1} \to D_n \mid n)$
of right adjoints in
$(p_n:D_{n+1} \to D_n \mid n)$
of right adjoints in
![]() $\mathbf{Top}_A$
, its limit in
$\mathbf{Top}_A$
, its limit in
![]() $\mathbf{Top}_0$
is the sub-space of
$\mathbf{Top}_0$
is the sub-space of
![]() $\prod_{n}D_n$
corresponding to the subset
$\prod_{n}D_n$
corresponding to the subset
![]() $\lvert\thinspace {D} \thinspace\rvert\stackrel{\triangle}{=}\{d \mid \forall n.d_n=p_n(d_{n+1})\}$
, and the maps
$\lvert\thinspace {D} \thinspace\rvert\stackrel{\triangle}{=}\{d \mid \forall n.d_n=p_n(d_{n+1})\}$
, and the maps
![]() $\pi_n:D \to D_n$
with
$\pi_n:D \to D_n$
with
![]() $\pi_n(d)=d_n$
form a limit cone. Since
$\pi_n(d)=d_n$
form a limit cone. Since
![]() $U:\mathbf{Top}_0 \to \mathbf{Po}$
is
$U:\mathbf{Top}_0 \to \mathbf{Po}$
is
![]() $\mathbf{Po}$
-enriched and preserves limits, we have that
$\mathbf{Po}$
-enriched and preserves limits, we have that
![]() $(Up_n \mid n)$
is an
$(Up_n \mid n)$
is an
![]() $\omega^{op}$
-chain of right adjoints in
$\omega^{op}$
-chain of right adjoints in
![]() $\mathbf{Po}_A$
and
$\mathbf{Po}_A$
and
![]() $(U\pi_n \mid n)$
is a limit cone in
$(U\pi_n \mid n)$
is a limit cone in
![]() $\mathbf{Po}$
. By the result for
$\mathbf{Po}$
. By the result for
![]() $\mathbf{Po}_A$
, we have
$\mathbf{Po}_A$
, we have
![]() $UD:\mathbf{Po}_A$
. Hence,
$UD:\mathbf{Po}_A$
. Hence,
![]() $D:\mathbf{Top}_A$
.
$D:\mathbf{Top}_A$
.
A similar result holds if right adjoints are replaced by left adjoints (i.e.,
![]() $\mathbf{Po}_A$
and
$\mathbf{Po}_A$
and
![]() $\mathbf{Top}_A$
have limits of
$\mathbf{Top}_A$
have limits of
![]() $\omega^{op}$
-chains of left adjoints). We recall further properties of adjunctions in
$\omega^{op}$
-chains of left adjoints). We recall further properties of adjunctions in
![]() $\mathbf{Po}$
-enriched categories (and in
$\mathbf{Po}$
-enriched categories (and in
![]() $\mathbf{Po}$
). Each of these properties has a dual, which we do not state explicitly.
$\mathbf{Po}$
). Each of these properties has a dual, which we do not state explicitly.
Proposition 2.16.
If
![]() $f\dashv g$
in a
$f\dashv g$
in a
![]() $\mathbf{Po}$
-enriched category
$\mathbf{Po}$
-enriched category
![]() $\mathbb{A}$
and
$\mathbb{A}$
and
![]() $f:X\to Y$
is monic, then
$f:X\to Y$
is monic, then
![]() $g\circ f=\text{id}_X$
.
$g\circ f=\text{id}_X$
.
Proof. Since
![]() $f\dashv g$
one has
$f\dashv g$
one has
![]() $f\circ g\circ f=f$
. When f is monic, this implies
$f\circ g\circ f=f$
. When f is monic, this implies
![]() $g\circ f=\text{id}_X$
.
$g\circ f=\text{id}_X$
.
In other words, if a left adjoint is monic, then it is split monic and its right adjoint is split epic.
Proposition 2.17.
If X is a complete lattice, then
![]() $f:\mathbf{Po}(X,Y)$
is a left adjoint iff f preserves sups.
$f:\mathbf{Po}(X,Y)$
is a left adjoint iff f preserves sups.
Proof. By the dual of the adjoint functor theorem Borceux (Reference Borceux1994, Theorem 3.3.3) for posets.
Proposition 2.18.
If Y is a complete lattice and X is a sub-poset of Y, then the inclusion
![]() $f:X \to Y$
is a left adjoint in
$f:X \to Y$
is a left adjoint in
![]() $\mathbf{Po}$
iff X is a complete lattice and sups in X are computed as in Y (i.e., f preserves sups).
$\mathbf{Po}$
iff X is a complete lattice and sups in X are computed as in Y (i.e., f preserves sups).
Proof. The right-to-left implication follows from Proposition 2.17. For the other implication, consider the right adjoint g to f. By Remark 2.14, f preserves sups and g preserves infs. Moreover, X has all infs (i.e., is a complete lattice), because
![]() $g\circ f=\text{id}_X$
(by Proposition 2.16) and
$g\circ f=\text{id}_X$
(by Proposition 2.16) and
![]() $\inf D=g(\inf f(D))$
for any subset D of X.
$\inf D=g(\inf f(D))$
for any subset D of X.
Definition 2.19. (Best Approximation) Given a subset X of a poset Y,
![]() $x \in X$
is the best X-approximation of
$x \in X$
is the best X-approximation of
![]() $y \in Y$
iff
$y \in Y$
iff
![]() $\forall x' \in X.x'\leq x\iff x'\leq y$
.
$\forall x' \in X.x'\leq x\iff x'\leq y$
.
A subset X of a poset Y can be identified with the sub-poset of Y with carrier X and the partial order inherited from Y. Then, the inclusion
![]() $f:X \to Y$
is a left adjoint in
$f:X \to Y$
is a left adjoint in
![]() $\mathbf{Po}$
exactly when every
$\mathbf{Po}$
exactly when every
![]() $y \in Y$
has a best X-approximation, and the right adjoint to f maps y to its best X-approximation. When Y is a complete lattice, Proposition 2.18 characterizes the subsets X of Y for which every
$y \in Y$
has a best X-approximation, and the right adjoint to f maps y to its best X-approximation. When Y is a complete lattice, Proposition 2.18 characterizes the subsets X of Y for which every
![]() $y \in Y$
has a best X-approximation.
$y \in Y$
has a best X-approximation.
We are mainly interested in the cases where Y is a complete lattice of analyses
![]() $\mathbf{Po}_A(\leq_1,\leq_2)$
and X is a sub-poset of the form
$\mathbf{Po}_A(\leq_1,\leq_2)$
and X is a sub-poset of the form
![]() $\mathbf{Top}_A(\tau_1,\tau_2)$
, where
$\mathbf{Top}_A(\tau_1,\tau_2)$
, where
![]() $\leq_i$
is the specialization order of the topology
$\leq_i$
is the specialization order of the topology
![]() $\tau_i$
. In these cases, the best X-approximations exist whenever the poset
$\tau_i$
. In these cases, the best X-approximations exist whenever the poset
![]() $\mathbf{Top}_A(\tau_1,\tau_2)$
is a complete lattice with sups computed as in
$\mathbf{Top}_A(\tau_1,\tau_2)$
is a complete lattice with sups computed as in
![]() $\mathbf{Po}_A(\leq_1,\leq_2)$
.
$\mathbf{Po}_A(\leq_1,\leq_2)$
.
Example 2.20. Given a complete lattice
![]() $\leq$
(on a set X), we can define two topologies in
$\leq$
(on a set X), we can define two topologies in
![]() $\mathbf{Top}(\leq)$
:
$\mathbf{Top}(\leq)$
:
-
(1) the Scott topology
 $\tau_S(\leq)$
of upward closed subsets O of X such that
$\tau_S(\leq)$
of upward closed subsets O of X such that
 $\sup D\in O\implies \exists d \in D.d\in O$
for any directed subset D of X, equivalently,
$\sup D\in O\implies \exists d \in D.d\in O$
for any directed subset D of X, equivalently,
 $\sup S\in O\implies\exists S_0\subseteq_f S.\sup S_0\in O$
for any subset S of X.
$\sup S\in O\implies\exists S_0\subseteq_f S.\sup S_0\in O$
for any subset S of X. -
(2) the
 $\omega$
-topology
$\omega$
-topology
 $\tau_\omega(\leq)$
of upward closed subsets O of X such that
$\tau_\omega(\leq)$
of upward closed subsets O of X such that
 $\sup D\in O\implies\exists d \in D.d\in O$
for any
$\sup D\in O\implies\exists d \in D.d\in O$
for any
 $\omega$
-chain D in X, equivalently,
$\omega$
-chain D in X, equivalently,
 $\sup S\in O\implies\exists S_0\subseteq_f S. \sup S_0\in O$
for any countable subset S of X.
$\sup S\in O\implies\exists S_0\subseteq_f S. \sup S_0\in O$
for any countable subset S of X.
Clearly,
![]() $\tau_S(\leq)\subseteq\tau_\omega(\leq)$
. Given a map
$\tau_S(\leq)\subseteq\tau_\omega(\leq)$
. Given a map
![]() $f:\mathbf{Po}_A(\leq_1,\leq_2)$
, there is an order-theoretic characterization of continuity with respect to these two topologies, namely:
$f:\mathbf{Po}_A(\leq_1,\leq_2)$
, there is an order-theoretic characterization of continuity with respect to these two topologies, namely:
-
 $f:\mathbf{Top}_A(\tau_S(\leq_1),\tau_S(\leq_2)) \iff f$
preserves sups of directed sets, i.e., f is Scott continuous.
$f:\mathbf{Top}_A(\tau_S(\leq_1),\tau_S(\leq_2)) \iff f$
preserves sups of directed sets, i.e., f is Scott continuous. -
 $f:\mathbf{Top}_A(\tau_\omega(\leq_1),\tau_\omega(\leq_2))\iff f$
preserves sups of
$f:\mathbf{Top}_A(\tau_\omega(\leq_1),\tau_\omega(\leq_2))\iff f$
preserves sups of
 $\omega$
-chains, i.e., f is
$\omega$
-chains, i.e., f is
 $\omega$
-continuous.
$\omega$
-continuous.
These characterizations imply
![]() $\mathbf{Top}_A(\tau_S(\leq_1),\tau_S(\leq_2))\subseteq \mathbf{Top}_A(\tau_\omega(\leq_1),\tau_\omega(\leq_2))\subseteq\mathbf{Po}_A(\leq_1,$
$\mathbf{Top}_A(\tau_S(\leq_1),\tau_S(\leq_2))\subseteq \mathbf{Top}_A(\tau_\omega(\leq_1),\tau_\omega(\leq_2))\subseteq\mathbf{Po}_A(\leq_1,$
![]() $\leq_2)$
and that these subsets are closed with respect to sups computed in
$\leq_2)$
and that these subsets are closed with respect to sups computed in
![]() $\mathbf{Po}_A(\leq_1,\leq_2)$
. Therefore, every analysis
$\mathbf{Po}_A(\leq_1,\leq_2)$
. Therefore, every analysis
![]() $f:\mathbf{Po}_A(\leq_1,\leq_2)$
has a best Scott-continuous approximation
$f:\mathbf{Po}_A(\leq_1,\leq_2)$
has a best Scott-continuous approximation
![]() $\Box_S(f)$
, and a best
$\Box_S(f)$
, and a best
![]() $\omega$
-continuous approximation
$\omega$
-continuous approximation
![]() $\Box_\omega(f)$
, with
$\Box_\omega(f)$
, with
![]() $\Box_S(f)\leq\Box_\omega(f)\leq f$
.
$\Box_S(f)\leq\Box_\omega(f)\leq f$
.
We introduce two sub-categories of
![]() $\mathbf{Po}_A$
, related to the example above.
$\mathbf{Po}_A$
, related to the example above.
Definition 2.21 (Category of Continuous Lattices (Gierz et al., Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott1980)).
-
 $\mathbf{CL}$
is the category of continuous lattices, i.e., every element x in the lattice is the sup of the directed set formed by the elements way-below x, and Scott-continuous maps.
$\mathbf{CL}$
is the category of continuous lattices, i.e., every element x in the lattice is the sup of the directed set formed by the elements way-below x, and Scott-continuous maps. -
 $\omega\mathbf{CL}$
is the full sub-category of
$\omega\mathbf{CL}$
is the full sub-category of
 $\mathbf{CL}$
whose objects are
$\mathbf{CL}$
whose objects are
 $\omega$
-continuous lattices, i.e., continuous lattices with a countable subset B (called a base) such that every element x in the lattice is the sup of the directed set formed by the elements in the base way-below x.
$\omega$
-continuous lattices, i.e., continuous lattices with a countable subset B (called a base) such that every element x in the lattice is the sup of the directed set formed by the elements in the base way-below x.
Proposition 2.22.
The
![]() $\mathbf{Po}$
-enriched categories in the following diagram have finite products and limits of
$\mathbf{Po}$
-enriched categories in the following diagram have finite products and limits of
![]() $\omega^{op}$
-chains of right adjoints and the functors preserve them:
$\omega^{op}$
-chains of right adjoints and the functors preserve them:
where the full&faithful functor from
![]() $\mathbf{CL}$
to
$\mathbf{CL}$
to
![]() $\mathbf{Top}_A$
maps a continuous lattice
$\mathbf{Top}_A$
maps a continuous lattice
![]() $\leq$
to the Scott topology
$\leq$
to the Scott topology
![]() $\tau_S(\leq)$
. Moreover, the categories
$\tau_S(\leq)$
. Moreover, the categories
![]() $\omega\mathbf{CL}$
and
$\omega\mathbf{CL}$
and
![]() $\mathbf{CL}$
have exponentials, the functor
$\mathbf{CL}$
have exponentials, the functor
![]() preserves them, and every
preserves them, and every
![]() $\omega$
-continuous map between
$\omega$
-continuous map between
![]() $\omega$
-continuous lattices is necessarily Scott continuous.
$\omega$
-continuous lattices is necessarily Scott continuous.
Proof. According to Abramsky and Jung (Reference Abramsky, Jung, Abramsky, Gabbay and Maibaum1994, Proposition 3.2.4), if
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are two directed-complete partial orders with bases
$D_2$
are two directed-complete partial orders with bases
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, respectively, then
$B_2$
, respectively, then
![]() $B_1 \times B_2$
forms a basis for
$B_1 \times B_2$
forms a basis for
![]() $D_1 \times D_2$
. In particular, if
$D_1 \times D_2$
. In particular, if
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are both countable, then so is
$B_2$
are both countable, then so is
![]() $B_1 \times B_2$
. This implies that both
$B_1 \times B_2$
. This implies that both
![]() $\omega\mathbf{CL}$
and
$\omega\mathbf{CL}$
and
![]() $\mathbf{CL}$
have finite products. Exponentials in
$\mathbf{CL}$
have finite products. Exponentials in
![]() $\mathbf{CL}$
are discussed in Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott1980, Section II-4). Scott continuity of
$\mathbf{CL}$
are discussed in Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott1980, Section II-4). Scott continuity of
![]() $\omega$
-continuous maps between
$\omega$
-continuous maps between
![]() $\omega$
-continuous lattices is proven in Abramsky and Jung (Reference Abramsky, Jung, Abramsky, Gabbay and Maibaum1994, Proposition 2.2.14).
$\omega$
-continuous lattices is proven in Abramsky and Jung (Reference Abramsky, Jung, Abramsky, Gabbay and Maibaum1994, Proposition 2.2.14).
2.4 From spaces to complete lattices
Given a topological space
![]() $\mathbb{S}$
, the set of closed subsets of
$\mathbb{S}$
, the set of closed subsets of
![]() $\mathbb{S}$
, ordered by reverse inclusion, forms a complete lattice
$\mathbb{S}$
, ordered by reverse inclusion, forms a complete lattice
![]() $\mathbb{C}(\mathbb{S})$
, with sups given by intersection. We introduce several topologies on these complete lattices, but first we give the main properties of
$\mathbb{C}(\mathbb{S})$
, with sups given by intersection. We introduce several topologies on these complete lattices, but first we give the main properties of
![]() $\mathbb{C}$
as a functor from
$\mathbb{C}$
as a functor from
![]() $\mathbf{Haus}$
to
$\mathbf{Haus}$
to
![]() $\mathbf{Po}_A$
.
$\mathbf{Po}_A$
.
Definition 2.23
The functor
![]() $\mathbb{C}:\mathbf{Haus} \to \mathbf{Po}_A$
is defined as follows:
$\mathbb{C}:\mathbf{Haus} \to \mathbf{Po}_A$
is defined as follows:
-
 $\mathbb{C}(\mathbb{S})$
is the complete lattice of closed subsets of
$\mathbb{C}(\mathbb{S})$
is the complete lattice of closed subsets of
 $\mathbb{S}$
under reverse inclusion.
$\mathbb{S}$
under reverse inclusion. -
If
 $f:\mathbf{Haus}(\mathbb{S},\mathbb{S}')$
, then the map
$f:\mathbf{Haus}(\mathbb{S},\mathbb{S}')$
, then the map
 $\mathbb{C}(f)\stackrel{\triangle}{=} f_*:\mathbf{Po}_A(\mathbb{C}(\mathbb{S}),\mathbb{C}(\mathbb{S}'))$
is given by
$\mathbb{C}(f)\stackrel{\triangle}{=} f_*:\mathbf{Po}_A(\mathbb{C}(\mathbb{S}),\mathbb{C}(\mathbb{S}'))$
is given by
 $f_*(C)=\overline{f(C)}$
, i.e., it maps C to the closure of the image of C along f.
$f_*(C)=\overline{f(C)}$
, i.e., it maps C to the closure of the image of C along f.
-
There is also a contravariant version, whose action on maps
 $f^*:\mathbf{Po}_A(\mathbb{C}(\mathbb{S}'),\mathbb{C}(\mathbb{S}))$
is given by
$f^*:\mathbf{Po}_A(\mathbb{C}(\mathbb{S}'),\mathbb{C}(\mathbb{S}))$
is given by
 $f^*(C')=f^{-1}(C')$
, i.e., it maps C’ to the inverse image of C’ along f.
$f^*(C')=f^{-1}(C')$
, i.e., it maps C’ to the inverse image of C’ along f.
Theorem 2.24.
If
![]() in
in
![]() $\mathbf{Haus}$
, then
$\mathbf{Haus}$
, then
![]() $f^*\dashv f_*$
in
$f^*\dashv f_*$
in
![]() $\mathbf{Po}_A$
.
$\mathbf{Po}_A$
.
Proof. See Moggi et al. (Reference Moggi, Farjudian, Duracz and Taha2018, Example 5.5).
Definition 2.25. (Topologies on
![]() $\mathbb{C}(\mathbb{S})$
(Moggi et al., Reference Moggi, Farjudian, Duracz and Taha2018).
$\mathbb{C}(\mathbb{S})$
(Moggi et al., Reference Moggi, Farjudian, Duracz and Taha2018).
-
(1) Given a Hausdorff space
 $\mathbb{S}$
, the upper Vietoris topology
$\mathbb{S}$
, the upper Vietoris topology
 $\tau_U(\mathbb{S})$
is the topology on
$\tau_U(\mathbb{S})$
is the topology on
 $\mathsf{C}(\mathbb{S})$
for which
$\mathsf{C}(\mathbb{S})$
for which
 $U \in \tau_U(\mathbb{S})\stackrel{\triangle}{\iff}\forall C \in U.\exists O \in \mathsf{O}(\mathbb{S}).C\in\uparrow O\subseteq U$
, where
$U \in \tau_U(\mathbb{S})\stackrel{\triangle}{\iff}\forall C \in U.\exists O \in \mathsf{O}(\mathbb{S}).C\in\uparrow O\subseteq U$
, where
 $\uparrow S\stackrel{\triangle}{=}\{C \in \mathsf{C}(\mathbb{S}) \mid C\subseteq S\}$
, i.e., the set of closed subsets of
$\uparrow S\stackrel{\triangle}{=}\{C \in \mathsf{C}(\mathbb{S}) \mid C\subseteq S\}$
, i.e., the set of closed subsets of
 $\mathbb{S}$
included in S.
$\mathbb{S}$
included in S. -
(2) Given an extended metric space
 $\mathbb{S}$
, the Robust topology
$\mathbb{S}$
, the Robust topology
 $\tau_R(\mathbb{S})$
is the topology on
$\tau_R(\mathbb{S})$
is the topology on
 $\mathsf{C}(\mathbb{S})$
for which
$\mathsf{C}(\mathbb{S})$
for which
 $U \in \tau_R(\mathbb{S})\stackrel{\triangle}{\iff}\forall C \in U.\exists \delta>0.C\in\uparrow B(C,\delta)\subseteq U$
, where
$U \in \tau_R(\mathbb{S})\stackrel{\triangle}{\iff}\forall C \in U.\exists \delta>0.C\in\uparrow B(C,\delta)\subseteq U$
, where
 $B(S,\delta) \in \mathsf{O}(\mathbb{S})$
is defined in Definition 2.5.
$B(S,\delta) \in \mathsf{O}(\mathbb{S})$
is defined in Definition 2.5.
-
(3) For uniformity, given a Hausdorff space
 $\mathbb{S}$
, we write
$\mathbb{S}$
, we write
 $\tau_S(\mathbb{S})$
and
$\tau_S(\mathbb{S})$
and
 $\tau_A(\mathbb{S})$
for the Scott and Alexandroff topologies on
$\tau_A(\mathbb{S})$
for the Scott and Alexandroff topologies on
 $\mathsf{C}(\mathbb{S})$
induced by the partial order on
$\mathsf{C}(\mathbb{S})$
induced by the partial order on
 $\mathbb{C}(\mathbb{S})$
, and for conciseness we write
$\mathbb{C}(\mathbb{S})$
, and for conciseness we write
 $\mathbb{A}_{\alpha \beta}(\mathbb{S}_1,\mathbb{S}_2)$
for the poset
$\mathbb{A}_{\alpha \beta}(\mathbb{S}_1,\mathbb{S}_2)$
for the poset
 $\mathbf{Top}_A(\tau_\alpha (\mathbb{S}_1),\tau_\beta(\mathbb{S}_2))$
, where
$\mathbf{Top}_A(\tau_\alpha (\mathbb{S}_1),\tau_\beta(\mathbb{S}_2))$
, where
 $\alpha$
and
$\alpha$
and
 $\beta$
range over
$\beta$
range over
 $\{A,R,S,U\}$
.
$\{A,R,S,U\}$
.
Remark 2.26. The Robust topology
![]() $\tau_R(\mathbb{S})$
on
$\tau_R(\mathbb{S})$
on
![]() $\mathsf{C}(\mathbb{S})$
induced by the metric d on
$\mathsf{C}(\mathbb{S})$
induced by the metric d on
![]() $\mathbb{S}$
coincides with the topology induced by the Hausdorff-Smyth hemi-metric d’ on
$\mathbb{S}$
coincides with the topology induced by the Hausdorff-Smyth hemi-metric d’ on
![]() $\mathsf{C}(\mathbb{S})$
induced by d, see Goubault-Larrecq (2008, Proposition 1).
$\mathsf{C}(\mathbb{S})$
induced by d, see Goubault-Larrecq (2008, Proposition 1).
Goubault-Larrecq defines
![]() $d'(C,C')\stackrel{\triangle}{=}\sup_{x' \in C'}\inf_{x \in C}d(x,x')$
under the assumption that d is a hemi-metric, i.e., d satisfies only the properties
$d'(C,C')\stackrel{\triangle}{=}\sup_{x' \in C'}\inf_{x \in C}d(x,x')$
under the assumption that d is a hemi-metric, i.e., d satisfies only the properties
![]() $d(x,x)=0$
and
$d(x,x)=0$
and
![]() $d(x,z)\leq d(x,y)+d(y,z)$
. However, unlike Proposition 1, we do not restrict d’ to the subset of
$d(x,z)\leq d(x,y)+d(y,z)$
. However, unlike Proposition 1, we do not restrict d’ to the subset of
![]() $\mathsf{C}(\mathbb{S})$
of the non-empty compact subsets, thus what is claimed in the proposition may fail for closed subsets.
$\mathsf{C}(\mathbb{S})$
of the non-empty compact subsets, thus what is claimed in the proposition may fail for closed subsets.
The topology induced by a hemi-metric d is the smallest topology containing all open balls
![]() $B(x,\delta)=\{x' \mid d(x,x')<\delta\}$
. Therefore, the topology induced by d’ on
$B(x,\delta)=\{x' \mid d(x,x')<\delta\}$
. Therefore, the topology induced by d’ on
![]() $\mathsf{C}(\mathbb{S})$
coincides with the Robust topology, because the following inclusions hold for every
$\mathsf{C}(\mathbb{S})$
coincides with the Robust topology, because the following inclusions hold for every
![]() $C \in \mathsf{C}(\mathbb{S})$
and
$C \in \mathsf{C}(\mathbb{S})$
and
![]() $0<\delta<\delta'$
$0<\delta<\delta'$
Theorem 2.27. The following statements hold:
-
(1) If
 $\mathbb{S}:\mathbf{Haus}$
, then
$\mathbb{S}:\mathbf{Haus}$
, then
 $\tau_U(\mathbb{S})$
is in
$\tau_U(\mathbb{S})$
is in
 $\mathbf{Top}(\leq)$
, where
$\mathbf{Top}(\leq)$
, where
 $\leq$
is the partial order on
$\leq$
is the partial order on
 $\mathbb{C}(\mathbb{S})$
.
$\mathbb{C}(\mathbb{S})$
. -
(2) If
 , then
, then
 $\mathbb{C}(\mathbb{S}):\mathbf{CL}$
and
$\mathbb{C}(\mathbb{S}):\mathbf{CL}$
and
 $\tau_U(\mathbb{S})=\tau_S(\mathbb{S})$
.
$\tau_U(\mathbb{S})=\tau_S(\mathbb{S})$
. -
(3) If
 $\mathbb{S}:\mathbf{Met}$
, then
$\mathbb{S}:\mathbf{Met}$
, then
 $\tau_S(\mathbb{S})\subseteq\tau_R(\mathbb{S})\subseteq\tau_U(\mathbb{S})$
. Therefore,
$\tau_S(\mathbb{S})\subseteq\tau_R(\mathbb{S})\subseteq\tau_U(\mathbb{S})$
. Therefore,
 $\tau_S(\mathbb{S})=\tau_R(\mathbb{S})=\tau_U(\mathbb{S})$
when
$\tau_S(\mathbb{S})=\tau_R(\mathbb{S})=\tau_U(\mathbb{S})$
when
 $\mathbb{S}:\mathbf{KMS}$
.
$\mathbb{S}:\mathbf{KMS}$
. -
(4) If
 $\mathbb{S}:\mathbf{KMS}$
is finite, then
$\mathbb{S}:\mathbf{KMS}$
is finite, then
 $\mathbb{C}(\mathbb{S})$
is finite and
$\mathbb{C}(\mathbb{S})$
is finite and
 $\tau_S(\mathbb{S})=\tau_A(\mathbb{S})$
.
$\tau_S(\mathbb{S})=\tau_A(\mathbb{S})$
.
Proof
-
(1) We prove that
 $\tau_\top\subseteq \tau_U(\mathbb{S})\subseteq\tau_\bot=\tau_A(\mathbb{S})$
(see Theorem 2.12).
$\tau_\top\subseteq \tau_U(\mathbb{S})\subseteq\tau_\bot=\tau_A(\mathbb{S})$
(see Theorem 2.12).
 $\tau_U(\mathbb{S})\subseteq\tau_A(\mathbb{S})$
, because the open subsets of the upper topology are upward closed with respect to reverse inclusion. To prove
$\tau_U(\mathbb{S})\subseteq\tau_A(\mathbb{S})$
, because the open subsets of the upper topology are upward closed with respect to reverse inclusion. To prove
 $\tau_\top\subseteq\tau_U(\mathbb{S})$
we show that
$\tau_\top\subseteq\tau_U(\mathbb{S})$
we show that
 $\not\downarrow C\stackrel{\triangle}{=}\{C' \in \mathsf{C}(\mathbb{S}) \mid C\not\subseteq C'\}$
is in
$\not\downarrow C\stackrel{\triangle}{=}\{C' \in \mathsf{C}(\mathbb{S}) \mid C\not\subseteq C'\}$
is in
 $\tau_U(\mathbb{S})$
when
$\tau_U(\mathbb{S})$
when
 $C \in \mathsf{C}(\mathbb{S})$
. If
$C \in \mathsf{C}(\mathbb{S})$
. If
 $C\not\subseteq C'$
, then there exists x in
$C\not\subseteq C'$
, then there exists x in
 $C-C'$
. But every singleton is closed in
$C-C'$
. But every singleton is closed in
 $\mathbb{S}$
(because
$\mathbb{S}$
(because
 $\mathbb{S}:\mathbf{Haus}$
), thus the complement O of the singleton
$\mathbb{S}:\mathbf{Haus}$
), thus the complement O of the singleton
 $\{x\}$
is open and
$\{x\}$
is open and
 $C'\in\uparrow O\subseteq\not\downarrow C$
.
$C'\in\uparrow O\subseteq\not\downarrow C$
. -
(2) Follows from Edalat (Reference Edalat1995, Proposition 3.3).
-
(3) The inclusions are proved in Moggi et al. (Reference Moggi, Farjudian, Duracz and Taha2018, Lemma A.3).
-
(4) If
 $\mathbb{S}$
is finite, then
$\mathbb{S}$
is finite, then
 $\mathbb{C}(\mathbb{S})$
is also finite. Hence,
$\mathbb{C}(\mathbb{S})$
is also finite. Hence,
 $\mathbf{Top}(\leq)$
contains only one topology.
$\mathbf{Top}(\leq)$
contains only one topology.
In item (3) of Theorem 2.27, when
![]() $\mathbb{S}$
is not compact, the inclusions may be strict. One such counter-example is the metric space
$\mathbb{S}$
is not compact, the inclusions may be strict. One such counter-example is the metric space
![]() $\mathbb{R}$
of real numbers.
$\mathbb{R}$
of real numbers.
Example 2.28. Let
![]() $\mathbb{R}$
be the metric space defined in Example 2.2, which is not compact. Consider the closed subset
$\mathbb{R}$
be the metric space defined in Example 2.2, which is not compact. Consider the closed subset
![]() $\mathbb{N}$
of natural numbers and the open subset
$\mathbb{N}$
of natural numbers and the open subset
![]() $O \stackrel{\triangle}{=} \bigcup_{n \in \mathbb{N}} B(n,2^{-(n+1)})$
, then:
$O \stackrel{\triangle}{=} \bigcup_{n \in \mathbb{N}} B(n,2^{-(n+1)})$
, then:
-
 $\uparrow\!{O}$
is in
$\uparrow\!{O}$
is in
 $\tau_U(\mathbb{R})$
, but it is not in
$\tau_U(\mathbb{R})$
, but it is not in
 $\tau_R(\mathbb{R})$
, because
$\tau_R(\mathbb{R})$
, because
 $\mathbb{N} \in \uparrow\!{O}$
, but there is no
$\mathbb{N} \in \uparrow\!{O}$
, but there is no
 $\delta>0$
such that
$\delta>0$
such that
 $B(\mathbb{N},\delta)\subseteq O$
. The reason is that, for any given
$B(\mathbb{N},\delta)\subseteq O$
. The reason is that, for any given
 $\delta > 0$
, if we take
$\delta > 0$
, if we take
 $n_0 \in \mathbb{N}$
to be large enough to satisfy
$n_0 \in \mathbb{N}$
to be large enough to satisfy
 $2^{-(n_0+1)} < \delta$
, then
$2^{-(n_0+1)} < \delta$
, then
 $B(n_0,\delta)\subseteq B(\mathbb{N},\delta)$
, but
$B(n_0,\delta)\subseteq B(\mathbb{N},\delta)$
, but
 $B(n_0,\delta)\not\subseteq O$
.
$B(n_0,\delta)\not\subseteq O$
. -
 $\uparrow\!{\emptyset}=\{\emptyset\}$
is in
$\uparrow\!{\emptyset}=\{\emptyset\}$
is in
 $\tau_R(\mathbb{R})$
, because
$\tau_R(\mathbb{R})$
, because
 $\forall \delta > 0.\ B(\emptyset,\delta)=\emptyset$
, but
$\forall \delta > 0.\ B(\emptyset,\delta)=\emptyset$
, but
 $\uparrow\!{\emptyset}$
is not in
$\uparrow\!{\emptyset}$
is not in
 $\tau_S(\mathbb{R})$
. The reason is that, if we define
$\tau_S(\mathbb{R})$
. The reason is that, if we define
 $C_n \stackrel{\triangle}{=} {{\{{x \in \mathbb{R}} \mid{x\geq 2^n}\}}}$
for every
$C_n \stackrel{\triangle}{=} {{\{{x \in \mathbb{R}} \mid{x\geq 2^n}\}}}$
for every
 $n \in \omega$
, then
$n \in \omega$
, then
 $(C_n \mid n \in \omega)$
is a chain of closed subsets of
$(C_n \mid n \in \omega)$
is a chain of closed subsets of
 $\mathbb{R}$
satisfying
$\mathbb{R}$
satisfying
 $\bigcap_{n \in \omega} C_n = \emptyset$
, but
$\bigcap_{n \in \omega} C_n = \emptyset$
, but
 $\forall n \in \omega.\ \emptyset \neq C_n$
.
$\forall n \in \omega.\ \emptyset \neq C_n$
.
Theorem 2.29.
If
![]() $f:\mathbf{Haus}(\mathbb{S},\mathbb{S}')$
, then
$f:\mathbf{Haus}(\mathbb{S},\mathbb{S}')$
, then
![]() $f^*:\mathbb{A}_{SS}(\mathbb{S}',\mathbb{S})$
and
$f^*:\mathbb{A}_{SS}(\mathbb{S}',\mathbb{S})$
and
![]() $f_*:\mathbb{A}_{UU}(\mathbb{S},\mathbb{S}')$
.
$f_*:\mathbb{A}_{UU}(\mathbb{S},\mathbb{S}')$
.
Proof. Since the map
![]() $f^*$
is a left adjoint in
$f^*$
is a left adjoint in
![]() $\mathbf{Po}_A$
, it preserves all sups. Thus, it is Scott continuous. The map
$\mathbf{Po}_A$
, it preserves all sups. Thus, it is Scott continuous. The map
![]() $f_*$
is upper Vietoris continuous, because for any
$f_*$
is upper Vietoris continuous, because for any
![]() $C \in \mathsf{C}(\mathbb{S})$
and
$C \in \mathsf{C}(\mathbb{S})$
and
![]() $O' \in \mathsf{O}(\mathbb{S}')$
we have
$O' \in \mathsf{O}(\mathbb{S}')$
we have
![]() $\overline{f(C)}\subseteq O'\implies f(C)\subseteq O'\implies C\subseteq f^{-1}(O')$
and
$\overline{f(C)}\subseteq O'\implies f(C)\subseteq O'\implies C\subseteq f^{-1}(O')$
and
![]() $f^{-1}(O') \in \mathsf{O}(\mathbb{S})$
by continuity of f.
$f^{-1}(O') \in \mathsf{O}(\mathbb{S})$
by continuity of f.
Theorem 2.30.
The functor
![]() $\mathbb{C}:\mathbf{Haus} \to \mathbf{Po}_A$
restricted to
$\mathbb{C}:\mathbf{Haus} \to \mathbf{Po}_A$
restricted to
![]() $\mathbf{KH}$
factors through
$\mathbf{KH}$
factors through
![]() $\mathbf{CL}$
, and when restricted to
$\mathbf{CL}$
, and when restricted to
![]() $\mathbf{KMS}$
, it factors through
$\mathbf{KMS}$
, it factors through
![]() $\omega\mathbf{CL}$
.
$\omega\mathbf{CL}$
.
Proof. From Theorem 2.27, we know that for any
![]() $X:\mathbf{KH}$
, the lattice
$X:\mathbf{KH}$
, the lattice
![]() $\mathbb{C}(X)$
is continuous. The fact that for any
$\mathbb{C}(X)$
is continuous. The fact that for any
![]() $X:\mathbf{KMS}$
, the lattice
$X:\mathbf{KMS}$
, the lattice
![]() $\mathbb{C}(X)$
is
$\mathbb{C}(X)$
is
![]() $\omega$
-continuous is a straightforward consequence. It remains to show that, if
$\omega$
-continuous is a straightforward consequence. It remains to show that, if
![]() $f:\mathbf{KH}(X,Y)$
, then
$f:\mathbf{KH}(X,Y)$
, then
![]() $f_*$
is Scott continuous. But this also follows from item (2) of Theorem 2.27 and Theorem 2.29.
$f_*$
is Scott continuous. But this also follows from item (2) of Theorem 2.27 and Theorem 2.29.
Example 2.31. Consider the compact Hausdorff spaces
![]() $\mathbb{R}_\infty$
and
$\mathbb{R}_\infty$
and
![]() $\overline{\mathbb{R}}$
defined in Example 2.2, i.e., the one-point and two-point compactifications of
$\overline{\mathbb{R}}$
defined in Example 2.2, i.e., the one-point and two-point compactifications of
![]() $\mathbb{R}$
. These spaces are related by the maps
$\mathbb{R}$
. These spaces are related by the maps
![]() in
in
![]() $\mathbf{Haus}$
, where
$\mathbf{Haus}$
, where
![]() $\overline{\iota}$
is the obvious sub-space inclusion and f maps
$\overline{\iota}$
is the obvious sub-space inclusion and f maps
![]() $-\infty$
and
$-\infty$
and
![]() $+\infty$
to
$+\infty$
to
![]() $\infty$
and is the identity on the other points. Moreover, the sub-space inclusion
$\infty$
and is the identity on the other points. Moreover, the sub-space inclusion
![]() is given by the composition
is given by the composition
![]() $f\circ\overline{\iota}$
. By Theorem 2.24, we get the adjunctions
$f\circ\overline{\iota}$
. By Theorem 2.24, we get the adjunctions
 in
in
![]() $\mathbf{Po}_A$
. Since
$\mathbf{Po}_A$
. Since
![]() $\overline{\iota}^*\circ\overline{\iota}_*$
is the identity on
$\overline{\iota}^*\circ\overline{\iota}_*$
is the identity on
![]() $\mathbb{C}(\mathbb{R})$
and
$\mathbb{C}(\mathbb{R})$
and
![]() $f_*\circ f^*$
is the identity on
$f_*\circ f^*$
is the identity on
![]() $\mathbb{C}(\mathbb{R}_\infty)$
, we conclude that
$\mathbb{C}(\mathbb{R}_\infty)$
, we conclude that
![]() $(\overline{\iota}_*,\overline{\iota}^*)$
is an insertion-closure pair and
$(\overline{\iota}_*,\overline{\iota}^*)$
is an insertion-closure pair and
![]() $(f^*,f_*)$
is an embedding-projection pair in
$(f^*,f_*)$
is an embedding-projection pair in
![]() $\mathbf{Po}_A$
. In fact,
$\mathbf{Po}_A$
. In fact,
![]() $(f^*,f_*)$
is an embedding-projection pair in
$(f^*,f_*)$
is an embedding-projection pair in
![]() $\mathbf{CL}$
, by Theorem 2.30. On the other hand,
$\mathbf{CL}$
, by Theorem 2.30. On the other hand,
![]() $\overline{\iota}_*$
is not Scott continuous, e.g., the sup of the
$\overline{\iota}_*$
is not Scott continuous, e.g., the sup of the
![]() $\omega$
-chain
$\omega$
-chain
![]() $([n,+\infty) \mid n \in \omega)$
in
$([n,+\infty) \mid n \in \omega)$
in
![]() $\mathbb{C}(\mathbb{R})$
is
$\mathbb{C}(\mathbb{R})$
is
![]() $\emptyset$
, while the sup of its image in
$\emptyset$
, while the sup of its image in
![]() $\mathbb{C}(\overline{\mathbb{R}})$
, namely
$\mathbb{C}(\overline{\mathbb{R}})$
, namely
![]() $([n,+\infty] \mid n \in \omega)$
, is the singleton
$([n,+\infty] \mid n \in \omega)$
, is the singleton
![]() $\{+\infty\}$
. However, by Theorem 2.29 and
$\{+\infty\}$
. However, by Theorem 2.29 and
![]() $\tau_U(\overline{\mathbb{R}})=\tau_S(\overline{\mathbb{R}})$
, we have that
$\tau_U(\overline{\mathbb{R}})=\tau_S(\overline{\mathbb{R}})$
, we have that
![]() $\overline{\iota}_*$
is in
$\overline{\iota}_*$
is in
![]() $\mathbb{A}_{US}(\mathbb{R},\overline{\mathbb{R}})$
. Furthermore, by the results in Section 3, we have that
$\mathbb{A}_{US}(\mathbb{R},\overline{\mathbb{R}})$
. Furthermore, by the results in Section 3, we have that
![]() $\overline{\iota}_*$
is in
$\overline{\iota}_*$
is in
![]() $\mathbb{A}_{RS}(\mathbb{R},\overline{\mathbb{R}})$
.
$\mathbb{A}_{RS}(\mathbb{R},\overline{\mathbb{R}})$
.
Theorem 2.32.
The functor
![]() $\mathbb{C}:\mathbf{KH} \to \mathbf{CL}$
preserves limits of
$\mathbb{C}:\mathbf{KH} \to \mathbf{CL}$
preserves limits of
![]() $\omega^{op}$
-chains.
$\omega^{op}$
-chains.
Proof. Given an
![]() $\omega^{op}$
-chain
$\omega^{op}$
-chain
![]() $(p_n:X_{n+1} \to X_n \mid n)$
in
$(p_n:X_{n+1} \to X_n \mid n)$
in
![]() $\mathbf{KH}$
, let
$\mathbf{KH}$
, let
![]() $(\pi_n:X\to X_n \mid n)$
be its limit in
$(\pi_n:X\to X_n \mid n)$
be its limit in
![]() $\mathbf{KH}$
(and
$\mathbf{KH}$
(and
![]() $\mathbf{Haus}$
), where X is the sub-space of
$\mathbf{Haus}$
), where X is the sub-space of
![]() $\prod_n X_n$
such that
$\prod_n X_n$
such that
![]() $\lvert\thinspace {X} \thinspace\rvert=\{x \mid \forall n. x_n=p_n(x_{n+1})\}$
. By Theorem 2.15, the limit of
$\lvert\thinspace {X} \thinspace\rvert=\{x \mid \forall n. x_n=p_n(x_{n+1})\}$
. By Theorem 2.15, the limit of
![]() $(\mathbb{C}(p_n) \mid n)$
in
$(\mathbb{C}(p_n) \mid n)$
in
![]() $\mathbf{Po}_A$
is given by
$\mathbf{Po}_A$
is given by
![]() $(\pi'_n:D\to D_n \mid n)$
, where
$(\pi'_n:D\to D_n \mid n)$
, where
![]() $D_n$
is
$D_n$
is
![]() $\mathbb{C}(X_n)$
and D is the sub-poset of
$\mathbb{C}(X_n)$
and D is the sub-poset of
![]() $\prod_nD_n$
such that
$\prod_nD_n$
such that
![]() $\lvert\thinspace {D} \thinspace\rvert=\{d \mid \forall n.d_n=\mathbb{C}(p_n)(d_{n+1})\}$
. But for spaces in
$\lvert\thinspace {D} \thinspace\rvert=\{d \mid \forall n.d_n=\mathbb{C}(p_n)(d_{n+1})\}$
. But for spaces in
![]() $\mathbf{KH}$
compact and closed subsets coincide, thus
$\mathbf{KH}$
compact and closed subsets coincide, thus
![]() $\mathbb{C}(p_n)(C)=p_n(C)$
, i.e., it is the image of C along
$\mathbb{C}(p_n)(C)=p_n(C)$
, i.e., it is the image of C along
![]() $p_n$
.
$p_n$
.
By the universal property of D, there exists a unique map
![]() $\phi:\mathbb{C}(X) \to D$
in
$\phi:\mathbb{C}(X) \to D$
in
![]() $\mathbf{Po}_A$
such that:
$\mathbf{Po}_A$
such that:
namely
![]() $\phi(C)=(\pi_n(C) \mid n)$
for every
$\phi(C)=(\pi_n(C) \mid n)$
for every
![]() $C \in \mathbb{C}(X)$
. Moreover,
$C \in \mathbb{C}(X)$
. Moreover,
![]() $\phi$
preserves infs, since the
$\phi$
preserves infs, since the
![]() $\mathbb{C}(\pi_n)$
are right adjoints and preserve infs. Therefore,
$\mathbb{C}(\pi_n)$
are right adjoints and preserve infs. Therefore,
![]() $\phi$
has a left adjoint
$\phi$
has a left adjoint
![]() $\phi':D \to \mathbb{C}(X)$
, namely
$\phi':D \to \mathbb{C}(X)$
, namely
![]() $\phi'(d)=\bigcap_n\pi_n^*(d_n)$
. We prove that
$\phi'(d)=\bigcap_n\pi_n^*(d_n)$
. We prove that
![]() $\phi'$
is the inverse of
$\phi'$
is the inverse of
![]() $\phi$
, and the limit in
$\phi$
, and the limit in
![]() $\mathbf{Po}_A$
is actually in
$\mathbf{Po}_A$
is actually in
![]() $\mathbf{CL}$
, because
$\mathbf{CL}$
, because
![]() $\mathbf{CL}$
is replete in
$\mathbf{CL}$
is replete in
![]() $\mathbf{Po}_A$
(i.e., if
$\mathbf{Po}_A$
(i.e., if
![]() $A:\mathbf{CL}$
and
$A:\mathbf{CL}$
and
![]() $f:A\to B$
is an iso in
$f:A\to B$
is an iso in
![]() $\mathbf{Po}_A$
, then f is in
$\mathbf{Po}_A$
, then f is in
![]() $\mathbf{CL}$
). Because of the adjunction
$\mathbf{CL}$
). Because of the adjunction
![]() $\phi'\dashv\phi$
we have:
$\phi'\dashv\phi$
we have:
-
(1)
 $\forall n.\forall d \in D.\phi(\phi'(d))_n=\pi_n(\bigcap_n\pi_n^*(d_n))\subseteq d_n$
, and
$\forall n.\forall d \in D.\phi(\phi'(d))_n=\pi_n(\bigcap_n\pi_n^*(d_n))\subseteq d_n$
, and -
(2)
 $\forall C \in \mathbb{C}(X).C\subseteq\phi'(\phi(C))=\bigcap_n\pi_n^*(\pi_n(C))$
.
$\forall C \in \mathbb{C}(X).C\subseteq\phi'(\phi(C))=\bigcap_n\pi_n^*(\pi_n(C))$
.
We prove that the inclusions in (1) and (2) are indeed equalities. In the case of (1), given
![]() $d \in D$
, we have (by the Axiom of Choice)
$d \in D$
, we have (by the Axiom of Choice)
![]() $\forall n.\forall x \in d_n.\exists y \in d_{n+1}.x=p_n(y)$
, which leads to the construction of a sequence
$\forall n.\forall x \in d_n.\exists y \in d_{n+1}.x=p_n(y)$
, which leads to the construction of a sequence
![]() $\hat{y} \in X$
, from which we obtain:
$\hat{y} \in X$
, from which we obtain:
![]() $\forall n.\forall x \in d_n.\exists \hat{y} \in X.x=\hat{y}_n\land(\forall i.\hat{y}_i\in d_i)$
. But
$\forall n.\forall x \in d_n.\exists \hat{y} \in X.x=\hat{y}_n\land(\forall i.\hat{y}_i\in d_i)$
. But
![]() $\{\hat{y} \in X \mid \forall n.\hat{y}_n\in d_n\}$
is another way of denoting
$\{\hat{y} \in X \mid \forall n.\hat{y}_n\in d_n\}$
is another way of denoting
![]() $\bigcap_n\pi_n^*(d_n) \in \mathbb{C}(X)$
. Thus, the first inclusion is an equality.
$\bigcap_n\pi_n^*(d_n) \in \mathbb{C}(X)$
. Thus, the first inclusion is an equality.
In the case of (2), given an
![]() $x\in\phi'(\phi(C))$
, i.e.,
$x\in\phi'(\phi(C))$
, i.e.,
![]() $\forall n.x_n\in\pi'_n(C)$
, we prove that
$\forall n.x_n\in\pi'_n(C)$
, we prove that
![]() $x\in C$
. Since C is closed and a base for the topology on X is given by the subsets
$x\in C$
. Since C is closed and a base for the topology on X is given by the subsets
![]() $[O]_n=\{y \in X \mid y_n\in O\}$
with
$[O]_n=\{y \in X \mid y_n\in O\}$
with
![]() $O \in \mathsf{O}(X_n)$
, it suffices to prove that
$O \in \mathsf{O}(X_n)$
, it suffices to prove that
![]() $\forall n.\forall O \in \mathsf{O}(X_n).x\in[O]_n\implies\exists y \in C.y\in[O]_n$
. But,
$\forall n.\forall O \in \mathsf{O}(X_n).x\in[O]_n\implies\exists y \in C.y\in[O]_n$
. But,
![]() $x_n\in\pi_n(C)$
means that
$x_n\in\pi_n(C)$
means that
![]() $x_n=y_n$
for some
$x_n=y_n$
for some
![]() $y\in C$
. Hence,
$y\in C$
. Hence,
![]() $x\in [O]_n\iff x_n\in O\iff y_n\in O\iff y\in [O]_n$
.
$x\in [O]_n\iff x_n\in O\iff y_n\in O\iff y\in [O]_n$
.
3. Main Results
Ideally, given a metric space
![]() $\mathbb{S}$
(or more generally, an extended metric space), we would like to find a compactification
$\mathbb{S}$
(or more generally, an extended metric space), we would like to find a compactification
![]() $\overline{\mathbb{S}}$
of
$\overline{\mathbb{S}}$
of
![]() $\mathbb{S}$
such that the complete lattice
$\mathbb{S}$
such that the complete lattice
![]() $\mathbb{C}(\overline{\mathbb{S}})$
is
$\mathbb{C}(\overline{\mathbb{S}})$
is
![]() $\omega$
-continuous. For this, it suffices for the topology on
$\omega$
-continuous. For this, it suffices for the topology on
![]() $\overline{\mathbb{S}}$
to be second-countable, i.e., to have a countable base. Compactification, however, may not always give us the desired result. For instance, when
$\overline{\mathbb{S}}$
to be second-countable, i.e., to have a countable base. Compactification, however, may not always give us the desired result. For instance, when
![]() $\mathbb{S}$
is the sequence space
$\mathbb{S}$
is the sequence space
![]() $\ell_{\infty}$
(see Section 4.4)—which is not second-countable—it is impossible to obtain an
$\ell_{\infty}$
(see Section 4.4)—which is not second-countable—it is impossible to obtain an
![]() $\omega$
-continuous lattice
$\omega$
-continuous lattice
![]() $\mathbb{C}(\overline{\mathbb{S}})$
if
$\mathbb{C}(\overline{\mathbb{S}})$
if
![]() $\overline{\mathbb{S}}$
is taken to be any compactification of
$\overline{\mathbb{S}}$
is taken to be any compactification of
![]() $\ell_{\infty}$
.
$\ell_{\infty}$
.
We establish a weaker result, namely given an
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n\mid n)$
of short idempotents (with certain additional properties) on a metric space
$(g_n\mid n)$
of short idempotents (with certain additional properties) on a metric space
![]() $\mathbb{S}$
, we define a compact Hausdorff space
$\mathbb{S}$
, we define a compact Hausdorff space
![]() $\overline{\mathbb{S}}$
with a countable base and a continuous map
$\overline{\mathbb{S}}$
with a countable base and a continuous map
![]() $\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
such that the monotonic map
$\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
such that the monotonic map
![]() $\mathbb{C}(\iota):\mathbb{C}(\mathbb{S})\to \mathbb{C}(\overline{\mathbb{S}})$
is continuous when
$\mathbb{C}(\iota):\mathbb{C}(\mathbb{S})\to \mathbb{C}(\overline{\mathbb{S}})$
is continuous when
![]() $\mathbb{C}(\mathbb{S})$
is equipped with the Robust topology and
$\mathbb{C}(\mathbb{S})$
is equipped with the Robust topology and
![]() $\mathbb{C}(\overline{\mathbb{S}})$
is equipped with the Scott topology. In general,
$\mathbb{C}(\overline{\mathbb{S}})$
is equipped with the Scott topology. In general,
![]() $\overline{\mathbb{S}}$
is not a compactification of
$\overline{\mathbb{S}}$
is not a compactification of
![]() $\mathbb{S}$
, nor is it uniquely determined (up to iso) by
$\mathbb{S}$
, nor is it uniquely determined (up to iso) by
![]() $\mathbb{S}$
, as it depends on the choice of
$\mathbb{S}$
, as it depends on the choice of
![]() $(g_n \mid n)$
.
$(g_n \mid n)$
.
The result above follows from Theorem 3.10, which is applicable under more general assumptions than having an
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
of short idempotents. Another result, Theorem 3.11, gives sufficient conditions to ensure that
$(g_n \mid n)$
of short idempotents. Another result, Theorem 3.11, gives sufficient conditions to ensure that
![]() $\iota\,:\,\mathbb{S}\to\overline{\mathbb{S}}$
is both monic and epic, which is as close as we can get to having that
$\iota\,:\,\mathbb{S}\to\overline{\mathbb{S}}$
is both monic and epic, which is as close as we can get to having that
![]() $\overline{\mathbb{S}}$
is a compactification of
$\overline{\mathbb{S}}$
is a compactification of
![]() $\mathbb{S}$
.
$\mathbb{S}$
.
3.1 Idempotents, sections, and retractions
In this section, we establish some general properties of idempotents, sections (aka split monos), and retractions (aka split epis). All these notions are preserved by functors and reflected by full&faithful functors. The properties of section-retraction pairs that we consider are weaker variants of those considered in Domain Theory for embedding-projection pairs, such as the limit-colimit coincidence, see e.g., Abramsky and Jung (Reference Abramsky, Jung, Abramsky, Gabbay and Maibaum1994, Sec 3.3.2). The notion of embedding-projection pair (and insertion-closure pair) is available only in
![]() $\mathbf{Po}$
-enriched categories, see e.g., Abramsky and Jung (Reference Abramsky, Jung, Abramsky, Gabbay and Maibaum1994, Sec 3.1). Therefore, in the categories (of spaces) that we consider, one can rely only on the more general notion of section-retraction pair.
$\mathbf{Po}$
-enriched categories, see e.g., Abramsky and Jung (Reference Abramsky, Jung, Abramsky, Gabbay and Maibaum1994, Sec 3.1). Therefore, in the categories (of spaces) that we consider, one can rely only on the more general notion of section-retraction pair.
Definition 3.1 (idempotents co) In a category
![]() $\mathbb{A}$
:
$\mathbb{A}$
:
-
(1) g is an idempotent on X
 and
and
 $g\circ g=g$
.
$g\circ g=g$
. -
(2) given two idempotents
 $g_1$
and
$g_1$
and
 $g_2$
on X we write
$g_2$
on X we write
 $g_1\leq g_2\stackrel{\triangle}{\iff} g_1\circ g_2 = g_1 = g_2\circ g_1$
.
$g_1\leq g_2\stackrel{\triangle}{\iff} g_1\circ g_2 = g_1 = g_2\circ g_1$
. -
(3) (e,p) is an sr-pair (sr for section-retraction) from X to
 $Y\stackrel{\triangle}{\iff}$
$Y\stackrel{\triangle}{\iff}$
 and
and
 $p\circ e=\text{id}_X$
.
$p\circ e=\text{id}_X$
. -
(4) (e,p) is a splitting of g
 $\stackrel{\triangle}{\iff}$
(e,p) is an sr-pair such that
$\stackrel{\triangle}{\iff}$
(e,p) is an sr-pair such that
 $g=e\circ p$
.
$g=e\circ p$
. -
(5) idempotents split
 $\stackrel{\triangle}{\iff}$
every idempotent has a splitting.
$\stackrel{\triangle}{\iff}$
every idempotent has a splitting.
We write
![]() $\mathbb{I}(X)$
for the poset of idempotents on X and
$\mathbb{I}(X)$
for the poset of idempotents on X and
![]() $\mathbb{A}_{sr}$
for the category with sr-pairs as arrows.
$\mathbb{A}_{sr}$
for the category with sr-pairs as arrows.
When
![]() $\mathbb{A}$
is
$\mathbb{A}$
is
![]() $\mathbf{Po}$
-enriched, there is a partial order
$\mathbf{Po}$
-enriched, there is a partial order
![]() $\sqsubseteq$
on the hom-set
$\sqsubseteq$
on the hom-set
![]() $\mathbb{A}(X,X)$
of endomorphisms on X, but its restriction to the subset of idempotents on X is unrelated to the partial order
$\mathbb{A}(X,X)$
of endomorphisms on X, but its restriction to the subset of idempotents on X is unrelated to the partial order
![]() $\leq$
. However, the two partial orders coincide when restricted to the idempotents below
$\leq$
. However, the two partial orders coincide when restricted to the idempotents below
![]() $\text{id}_X$
, i.e., the idempotents g such that
$\text{id}_X$
, i.e., the idempotents g such that
![]() $g\sqsubseteq\text{id}_X$
.
$g\sqsubseteq\text{id}_X$
.
In Category Theory, a definition or result given for a generic category
![]() $\mathbb{A}$
can be recast in the dual category
$\mathbb{A}$
can be recast in the dual category
![]() $\mathbb{A}^{op}$
. In particular, sections are the dual of retractions and idempotents are self-dual.
$\mathbb{A}^{op}$
. In particular, sections are the dual of retractions and idempotents are self-dual.
Proposition 3.2. (Duality).
The following statements hold:
-
(1) The definition of
 $g_1\leq g_2$
is self-dual, i.e.,
$g_1\leq g_2$
is self-dual, i.e.,
 $g_1\leq g_2$
in
$g_1\leq g_2$
in
 $\mathbb{A}$
$\mathbb{A}$
 $\iff$
$\iff$
 $g_1\leq g_2$
in
$g_1\leq g_2$
in
 $\mathbb{A}^{op}$
.
$\mathbb{A}^{op}$
. -
(2) (e,p) is an sr-pair from X to Y in
 $\mathbb{A}$
$\mathbb{A}$
 $\iff$
(p,e) is an sr-pair from X to Y in
$\iff$
(p,e) is an sr-pair from X to Y in
 $\mathbb{A}^{op}$
.
$\mathbb{A}^{op}$
.
The definition of epic (and monic) generalizes from maps (aka arrows) to families of maps.
Definition 3.3.
We say that the family of maps
![]() $(h_i:X_i\to X \mid i:I)$
into X is jointly epic in
$(h_i:X_i\to X \mid i:I)$
into X is jointly epic in
![]() $\mathbb{A}$
$\mathbb{A}$
![]() $\stackrel{\triangle}{\iff}$
$\stackrel{\triangle}{\iff}$
Dually, we say that the family of maps
![]() $(h_i:X\to X_i \mid i \in I)$
from X is jointly monic in
$(h_i:X\to X_i \mid i \in I)$
from X is jointly monic in
![]() $\mathbb{A}$
$\mathbb{A}$
![]() $\stackrel{\triangle}{\iff}$
$\stackrel{\triangle}{\iff}$
The family
![]() $(h_i \mid i \in I)$
determines X, provided I is not empty. As expected, a family consisting of one map h (i.e., I is a singleton) is jointly epic exactly when h is epic. The following proposition extends well-known properties of epis (namely,
$(h_i \mid i \in I)$
determines X, provided I is not empty. As expected, a family consisting of one map h (i.e., I is a singleton) is jointly epic exactly when h is epic. The following proposition extends well-known properties of epis (namely,
![]() $h\circ g$
epic implies h epic, and compositions of epis are epic) to families of maps.
$h\circ g$
epic implies h epic, and compositions of epis are epic) to families of maps.
Proposition 3.4.
Given a family of maps
![]() $(h_i:X_i\to X \mid i \in I)$
into X and for each
$(h_i:X_i\to X \mid i \in I)$
into X and for each
![]() $i \in I$
a family of maps
$i \in I$
a family of maps
![]() $(g_{i,j}:X_{i,j}\to X_i \mid j \in J_i)$
into
$(g_{i,j}:X_{i,j}\to X_i \mid j \in J_i)$
into
![]() $X_i$
, let
$X_i$
, let
![]() $(f_{i,j}:X_{i,j}\to X \mid i \in I, j \in J_i)$
be the family of maps into X such that
$(f_{i,j}:X_{i,j}\to X \mid i \in I, j \in J_i)$
be the family of maps into X such that
![]() $f_{i,j}=h_i\circ g_{i,j}$
. The following properties hold:
$f_{i,j}=h_i\circ g_{i,j}$
. The following properties hold:
-
(1) if
 $(h_i \mid i \in I)$
is jointly epic and
$(h_i \mid i \in I)$
is jointly epic and
 $(g_{i,j} \mid j \in J_i)$
is jointly epic for each
$(g_{i,j} \mid j \in J_i)$
is jointly epic for each
 $i \in I$
, then
$i \in I$
, then
 $(f_{i,j} \mid i \in I, j \in J_i)$
is jointly epic.
$(f_{i,j} \mid i \in I, j \in J_i)$
is jointly epic. -
(2) if
 $(f_{i,j} \mid i \in I,j \in J_i)$
is jointly epic, then
$(f_{i,j} \mid i \in I,j \in J_i)$
is jointly epic, then
 $(h_i \mid i \in I)$
is jointly epic.
$(h_i \mid i \in I)$
is jointly epic.
Moreover, if
![]() $(h_i:X_i\to X \mid i \in I)$
is a colimit cone from some diagram D in
$(h_i:X_i\to X \mid i \in I)$
is a colimit cone from some diagram D in
![]() $\mathbb{A}$
to X, then the family of maps
$\mathbb{A}$
to X, then the family of maps
![]() $(h_i \mid i \in I)$
into X is jointly epic.
$(h_i \mid i \in I)$
into X is jointly epic.
Proposition 3.5. (Basic facts). In any category
![]() $\mathbb{A}$
, the following hold:
$\mathbb{A}$
, the following hold:
-
(1) the relation
 $\leq$
is a partial order on
$\leq$
is a partial order on
 $\mathbb{I}(X)$
, i.e.,
$\mathbb{I}(X)$
, i.e.,
 $g_1\leq g_2\leq g_1\implies g_1=g_2$
and
$g_1\leq g_2\leq g_1\implies g_1=g_2$
and
 $g_1\leq g_2\leq g_3\implies g_1\leq g_3$
, and
$g_1\leq g_2\leq g_3\implies g_1\leq g_3$
, and
 $\text{id}_X$
is the top element in
$\text{id}_X$
is the top element in
 $\mathbb{I}(X)$
, i.e.,
$\mathbb{I}(X)$
, i.e.,
 $g\leq\text{id}_X$
for g idempotent on X.
$g\leq\text{id}_X$
for g idempotent on X. -
(2) if (e,p) is an sr-pair from X to Y, then
 $g=e\circ p$
is an idempotent on Y.
$g=e\circ p$
is an idempotent on Y.
-
(3) if
 $(g_i \mid i \in I)$
is a family in
$(g_i \mid i \in I)$
is a family in
 $\mathbb{I}(X)$
which is jointly monic (or jointly epic) in
$\mathbb{I}(X)$
which is jointly monic (or jointly epic) in
 $\mathbb{A}$
, then its sup in
$\mathbb{A}$
, then its sup in
 $\mathbb{I}(X)$
is
$\mathbb{I}(X)$
is
 $\text{id}_X$
.
$\text{id}_X$
. -
(4) all arrows in
 $\mathbb{A}_{sr}$
are monic, and (e,p) is an iso in
$\mathbb{A}_{sr}$
are monic, and (e,p) is an iso in
 $\mathbb{A}_{sr}\iff p$
is the inverse of e in
$\mathbb{A}_{sr}\iff p$
is the inverse of e in
 $\mathbb{A}$
.
$\mathbb{A}$
. -
(5)
 is a splitting of the idempotent
is a splitting of the idempotent
 $g_i:\mathbb{I}(Y)$
(for
$g_i:\mathbb{I}(Y)$
(for
 $i=1,2$
), then
$i=1,2$
), then
 $g_1\leq g_2\iff$
there exists, necessarily unique,
$g_1\leq g_2\iff$
there exists, necessarily unique,
 $(e,p):X_1\to X_2$
such that
$(e,p):X_1\to X_2$
such that
 $(e_1,p_1)=(e_2,p_2)\circ(e,p)$
.
$(e_1,p_1)=(e_2,p_2)\circ(e,p)$
.
Item (3).
Consider an idempotent g of X which is an upper-bound of
![]() $(g_i \mid i)$
, i.e.,
$(g_i \mid i)$
, i.e.,
![]() $\forall i.g_i\leq g$
. Then,
$\forall i.g_i\leq g$
. Then,
![]() $\forall i.g_i\circ g=g_i$
, which implies
$\forall i.g_i\circ g=g_i$
, which implies
![]() $g=\text{id}_X$
, because
$g=\text{id}_X$
, because
![]() $(g_i \mid i)$
is jointly monic.
$(g_i \mid i)$
is jointly monic.
Item (4).
To prove that any arrow (e,p) in
![]() $\mathbb{A}_{sr}$
is a mono, it suffices to observe that in
$\mathbb{A}_{sr}$
is a mono, it suffices to observe that in
![]() $\mathbb{A}$
every section e is monic and every retraction p is epic. If (e’,p’) is the inverse of (e,p) in
$\mathbb{A}$
every section e is monic and every retraction p is epic. If (e’,p’) is the inverse of (e,p) in
![]() $\mathbb{A}_{sr}$
, then e’ is the inverse of e in
$\mathbb{A}_{sr}$
, then e’ is the inverse of e in
![]() $\mathbb{A}$
, thus
$\mathbb{A}$
, thus
![]() $p=p\circ e\circ e'=e'$
, because
$p=p\circ e\circ e'=e'$
, because
![]() $p\circ e=\text{id}_X$
.
$p\circ e=\text{id}_X$
.
Item (5).
Uniqueness of (e,p) is immediate, because
![]() $(e_2,p_2)$
is a mono in
$(e_2,p_2)$
is a mono in
![]() $\mathbb{A}_{sr}$
. For existence, define
$\mathbb{A}_{sr}$
. For existence, define
![]() $e=p_2\circ e_1$
and
$e=p_2\circ e_1$
and
![]() $p=p_1\circ e_2$
. Then, from the assumption
$p=p_1\circ e_2$
. Then, from the assumption
![]() $e_1\circ p_1=g_1\leq g_2=e_2\circ p_2$
we derive:
$e_1\circ p_1=g_1\leq g_2=e_2\circ p_2$
we derive:
-
(i)
 $p\circ e=\text{id}_{X_1}$
(i.e., (e,p) is an sr-pair), because
$p\circ e=\text{id}_{X_1}$
(i.e., (e,p) is an sr-pair), because $(p_1\circ e_2)\circ(p_2\circ e_1)=$
by definition of
$(p_1\circ e_2)\circ(p_2\circ e_1)=$
by definition of
 $g_2$
$g_2$
 $p_1\circ g_2\circ e_1=$
by
$p_1\circ g_2\circ e_1=$
by
 $(e_1,p_1)$
sr-pair
$(e_1,p_1)$
sr-pair $p_1\circ g_2\circ e_1\circ(p_1\circ e_1)=$
by definition of
$p_1\circ g_2\circ e_1\circ(p_1\circ e_1)=$
by definition of
 $g_1$
$g_1$
 $p_1\circ g_2\circ g_1\circ e_1=$
by
$p_1\circ g_2\circ g_1\circ e_1=$
by
 $g_1\leq g_2$
$g_1\leq g_2$
 $p_1\circ g_1\circ e_1=$
by definition of
$p_1\circ g_1\circ e_1=$
by definition of
 $g_1$
$g_1$
 $p_1\circ (e_1\circ p_1)\circ e_1=$
by
$p_1\circ (e_1\circ p_1)\circ e_1=$
by
 $(e_1,p_1)$
sr-pair
$(e_1,p_1)$
sr-pair $\text{id}_{X_1}\circ\text{id}_{X_1}=\text{id}_{X_1}$
$\text{id}_{X_1}\circ\text{id}_{X_1}=\text{id}_{X_1}$
-
(ii)
 $e_2\circ e=e_1$
, because
$e_2\circ e=e_1$
, because $e_2\circ(p_2\circ e_1)=$
by definition of
$e_2\circ(p_2\circ e_1)=$
by definition of
 $g_2$
$g_2$
 $g_2\circ e_1=$
by
$g_2\circ e_1=$
by
 $(e_1,p_1)$
sr-pair
$(e_1,p_1)$
sr-pair $g_2\circ e_1\circ(p_1\circ e_1)=$
by definition of
$g_2\circ e_1\circ(p_1\circ e_1)=$
by definition of
 $g_1$
$g_1$
 $g_2\circ g_1\circ e_1=$
by
$g_2\circ g_1\circ e_1=$
by
 $g_1\leq g_2$
$g_1\leq g_2$
 $g_1\circ e_1=$
by definition of
$g_1\circ e_1=$
by definition of
 $g_1$
$g_1$
 $(e_1\circ p_1)\circ e_1=e_1$
by
$(e_1\circ p_1)\circ e_1=e_1$
by
 $(e_1,p_1)$
sr-pair
$(e_1,p_1)$
sr-pair -
(iii)
 $p\circ p_2=p_1$
, dual of the previous proof.
$p\circ p_2=p_1$
, dual of the previous proof.
Proposition 3.6. (
![]() $\omega$
-colimits of sections). Given an
$\omega$
-colimits of sections). Given an
![]() $\omega$
-chain
$\omega$
-chain
![]() $((e_n,p_n):X_n\to X_{n+1} \mid n \in \omega)$
in
$((e_n,p_n):X_n\to X_{n+1} \mid n \in \omega)$
in
![]() $\mathbb{A}_{sr}$
and a colimit cone
$\mathbb{A}_{sr}$
and a colimit cone
![]() $(\underline{f}_n:X_n \to \underline{X} \mid n)$
in
$(\underline{f}_n:X_n \to \underline{X} \mid n)$
in
![]() $\mathbb{A}$
from the
$\mathbb{A}$
from the
![]() $\omega$
-chain
$\omega$
-chain
![]() $(e_n:X_n \to X_{n+1} \mid n)$
to
$(e_n:X_n \to X_{n+1} \mid n)$
to
![]() $\underline{X}$
, there exists a unique cone
$\underline{X}$
, there exists a unique cone
![]() $((\underline{f}_n,\underline{q}_n):X_n \to \underline{X} \mid n)$
in
$((\underline{f}_n,\underline{q}_n):X_n \to \underline{X} \mid n)$
in
![]() $\mathbb{A}_{sr}$
from the
$\mathbb{A}_{sr}$
from the
![]() $\omega$
-chain
$\omega$
-chain
![]() $((e_n,p_n) \mid n)$
to
$((e_n,p_n) \mid n)$
to
![]() $\underline{X}$
(see Figure 3
). If
$\underline{X}$
(see Figure 3
). If
![]() $\underline{g}_n$
is the idempotent
$\underline{g}_n$
is the idempotent
![]() $\underline{f}_n\circ\underline{q}_n$
on
$\underline{f}_n\circ\underline{q}_n$
on
![]() $\underline{X}$
, then
$\underline{X}$
, then
![]() $(\underline{g}_n \mid n)$
is an
$(\underline{g}_n \mid n)$
is an
![]() $\omega$
-chain in
$\omega$
-chain in
![]() $\mathbb{I}(\underline{X})$
and is jointly epic in
$\mathbb{I}(\underline{X})$
and is jointly epic in
![]() $\mathbb{A}$
.
$\mathbb{A}$
.

Figure 3. Partial diagrammatic recast of Proposition 3.6.
Proof. First, we define the family
![]() $(h_{i,j}:X_i \to X_j \mid i,j \in \omega)$
of maps in
$(h_{i,j}:X_i \to X_j \mid i,j \in \omega)$
of maps in
![]() $\mathbb{A}$
(by induction on
$\mathbb{A}$
(by induction on
![]() $|j-i|$
):
$|j-i|$
):
-
 $h_{i,i}$
is the identity on
$h_{i,i}$
is the identity on
 $X_i$
$X_i$
-
 $h_{i,j}=h_{i+1,j}\circ e_i$
when
$h_{i,j}=h_{i+1,j}\circ e_i$
when
 $i<j$
, thus
$i<j$
, thus
 $h_{i,i+1}=e_i$
$h_{i,i+1}=e_i$
-
 $h_{i,j}=p_j\circ h_{i,j+1}$
when
$h_{i,j}=p_j\circ h_{i,j+1}$
when
 $i>j$
, thus
$i>j$
, thus
 $h_{i+1,i}=p_i$
$h_{i+1,i}=p_i$
Second, we prove (by induction on
![]() $|j-i|$
) the property:
$|j-i|$
) the property:
:
-
case
 $i=j$
: immediate, since
$i=j$
: immediate, since
 $h_{i+1,i}=p_i$
and
$h_{i+1,i}=p_i$
and
 $h_{i,i+1}=e_i$
.
$h_{i,i+1}=e_i$
. -
case
 $i<j$
:
$i<j$
:
 $h_{i+1,j}\circ e_i=h_{i,j}$
by definition of
$h_{i+1,j}\circ e_i=h_{i,j}$
by definition of
 $h_{i,j}$
. For the other equality:
$h_{i,j}$
. For the other equality:-
 $h_{i,j}=$
by definition of
$h_{i,j}=$
by definition of
 $h_{i,j}$
$h_{i,j}$
-
 $h_{i+1,j}\circ e_i=$
by IH on
$h_{i+1,j}\circ e_i=$
by IH on
 $(i+1,j)$
$(i+1,j)$
-
 $p_j\circ h_{i+1,j+1}\circ e_i=$
by definition of
$p_j\circ h_{i+1,j+1}\circ e_i=$
by definition of
 $h_{i,j+1}$
$h_{i,j+1}$
-
 $p_j\circ h_{i,j+1}$
.
$p_j\circ h_{i,j+1}$
.
-
-
case
 $i>j$
:
$i>j$
:
 $h_{i,j}=p_j\circ h_{i,j+1}$
by definition of
$h_{i,j}=p_j\circ h_{i,j+1}$
by definition of
 $h_{i,j}$
. For the other equality:
$h_{i,j}$
. For the other equality:-
 $h_{i+1,j}\circ e_i=$
by definition of
$h_{i+1,j}\circ e_i=$
by definition of
 $h_{i+1,j}$
$h_{i+1,j}$
-
 $p_j\circ h_{i+1,j+1}\circ e_i=$
by IH on
$p_j\circ h_{i+1,j+1}\circ e_i=$
by IH on
 $(i,j+1)$
$(i,j+1)$
-
 $p_j\circ h_{i,j+1}=$
by definition of
$p_j\circ h_{i,j+1}=$
by definition of
 $h_{i,j}$
$h_{i,j}$
-
 $h_{i,j}$
.
$h_{i,j}$
.
-
Property (1) implies that
![]() $(h_{i,n} \mid i)$
is a cone in
$(h_{i,n} \mid i)$
is a cone in
![]() $\mathbb{A}$
from
$\mathbb{A}$
from
![]() $(e_i \mid i)$
to
$(e_i \mid i)$
to
![]() $X_n$
. Thus, there exists a unique
$X_n$
. Thus, there exists a unique
![]() $\underline{q}_n:X_n\to\underline{X}$
such that
$\underline{q}_n:X_n\to\underline{X}$
such that
![]() $\forall i.\underline{q}_n\circ \underline{f}_i=h_{i,n}$
. In particular,
$\forall i.\underline{q}_n\circ \underline{f}_i=h_{i,n}$
. In particular,
![]() $\underline{q}_n\circ \underline{f}_n=h_{n,n}=\text{id}_{X_n}$
, i.e.,
$\underline{q}_n\circ \underline{f}_n=h_{n,n}=\text{id}_{X_n}$
, i.e.,
![]() $(\underline{f}_n,\underline{q}_n):X_n\to \underline{X}$
in
$(\underline{f}_n,\underline{q}_n):X_n\to \underline{X}$
in
![]() $\mathbb{A}_{sr}$
. Since the colimit cone
$\mathbb{A}_{sr}$
. Since the colimit cone
![]() $(\underline{f}_n \mid n)$
is jointly epic (by Proposition 3.4), property (1) implies also that
$(\underline{f}_n \mid n)$
is jointly epic (by Proposition 3.4), property (1) implies also that
![]() $\underline{q}_n=p_n\circ \underline{q}_{n+1}$
Thus,
$\underline{q}_n=p_n\circ \underline{q}_{n+1}$
Thus,
![]() $((\underline{f}_n,\underline{q}_n) \mid n)$
is a cone in
$((\underline{f}_n,\underline{q}_n) \mid n)$
is a cone in
![]() $\mathbb{A}_{sr}$
from
$\mathbb{A}_{sr}$
from
![]() $((e_n,p_n) \mid n)$
to
$((e_n,p_n) \mid n)$
to
![]() $\underline{X}$
.
$\underline{X}$
.
For uniqueness of
![]() $(\underline{q}_n \mid n)$
, we use again that
$(\underline{q}_n \mid n)$
, we use again that
![]() $(\underline{f}_n \mid n)$
is jointly epic and prove (by induction on
$(\underline{f}_n \mid n)$
is jointly epic and prove (by induction on
![]() $|j-i|$
) that
$|j-i|$
) that
![]() $\forall i,j.q'_j\circ \underline{f}_i=h_{i,j}$
when
$\forall i,j.q'_j\circ \underline{f}_i=h_{i,j}$
when
![]() $(q'_n \mid n)$
is a cone from
$(q'_n \mid n)$
is a cone from
![]() $\underline{X}$
to
$\underline{X}$
to
![]() $(p_n \mid n)$
such that
$(p_n \mid n)$
such that
![]() $\forall n.q'_n\circ \underline{f}_n=\text{id}_{X_n}$
.
$\forall n.q'_n\circ \underline{f}_n=\text{id}_{X_n}$
.
-
case
 $i=j$
: immediate, by
$i=j$
: immediate, by
 $q'_i\circ\underline{f}_i=\text{id}_{X_i}=h_{i,i}$
, assumption on
$q'_i\circ\underline{f}_i=\text{id}_{X_i}=h_{i,i}$
, assumption on
 $(q'_n \mid n)$
and definition of
$(q'_n \mid n)$
and definition of
 $h_{i,i}$
.
$h_{i,i}$
. -
case
 $i<j$
:
$i<j$
:-
 $q'_j\circ \underline{f}_i=$
by definition of
$q'_j\circ \underline{f}_i=$
by definition of
 $(\underline{f}_n \mid n)$
$(\underline{f}_n \mid n)$
-
 $q'_j\circ \underline{f}_{i+1}\circ e_i=$
by IH on
$q'_j\circ \underline{f}_{i+1}\circ e_i=$
by IH on
 $(i+1,j)$
$(i+1,j)$
-
 $h_{i+1,j}\circ e_i=h_{i,j}$
by definition of
$h_{i+1,j}\circ e_i=h_{i,j}$
by definition of
 $h_{i,j}$
.
$h_{i,j}$
.
-
-
case
 $i>j$
:
$i>j$
:-
 $q'_j\circ \underline{f}_i=$
by assumption on
$q'_j\circ \underline{f}_i=$
by assumption on
 $(q'_n \mid n)$
$(q'_n \mid n)$
-
 $p_j\circ q'_{j+1}\circ \underline{f}_i=$
by IH on
$p_j\circ q'_{j+1}\circ \underline{f}_i=$
by IH on
 $(i,j+1)$
$(i,j+1)$
-
 $p_j\circ h_{i,j+1}=h_{i,j}$
by definition of
$p_j\circ h_{i,j+1}=h_{i,j}$
by definition of
 $h_{i,j}$
.
$h_{i,j}$
.
-
Consider the idempotents
![]() $\underline{g}_n=\underline{f}_n\circ \underline{q}_n$
on
$\underline{g}_n=\underline{f}_n\circ \underline{q}_n$
on
![]() $\underline{X}$
. From item (5) of Proposition 3.5, it follows that
$\underline{X}$
. From item (5) of Proposition 3.5, it follows that
![]() $\forall n.\underline{g}_n\leq \underline{g}_{n+1}$
. Moreover, by Proposition 3.4, the family
$\forall n.\underline{g}_n\leq \underline{g}_{n+1}$
. Moreover, by Proposition 3.4, the family
![]() $(\underline{g}_n \mid n)$
is jointly epic, because it is the composition of jointly epic families, namely the colimit cone
$(\underline{g}_n \mid n)$
is jointly epic, because it is the composition of jointly epic families, namely the colimit cone
![]() $(\underline{f}_n \mid n)$
and the singleton families consisting of the (split) epic
$(\underline{f}_n \mid n)$
and the singleton families consisting of the (split) epic
![]() $\underline{q}_n$
.
$\underline{q}_n$
.
The following is the dual of Proposition 3.6:
Corollary 3.7. (
![]() $\omega^{op}$
-colimits of retractions).
$\omega^{op}$
-colimits of retractions).
Given an
![]() $\omega$
-chain
$\omega$
-chain
![]() $((e_n,p_n):X_n\to X_{n+1} \mid n \in \omega)$
, in
$((e_n,p_n):X_n\to X_{n+1} \mid n \in \omega)$
, in
![]() $\mathbb{A}_{sr}$
and a limit cone
$\mathbb{A}_{sr}$
and a limit cone
![]() $(\overline{q}_n: \overline{X}\to X_n \mid n)$
in
$(\overline{q}_n: \overline{X}\to X_n \mid n)$
in
![]() $\mathbb{A}$
from
$\mathbb{A}$
from
![]() $\overline{X}$
to the
$\overline{X}$
to the
![]() $\omega^{op}$
-chain
$\omega^{op}$
-chain
![]() $ (p_n:X_{n+1} \to X_n \mid n)$
, there exists a unique cone
$ (p_n:X_{n+1} \to X_n \mid n)$
, there exists a unique cone
![]() $((\overline{f}_n,\overline{q}_n):X_n \to \overline{X} \mid n)$
in
$((\overline{f}_n,\overline{q}_n):X_n \to \overline{X} \mid n)$
in
![]() $\mathbb{A}_{sr}$
from the
$\mathbb{A}_{sr}$
from the
![]() $\omega$
-chain
$\omega$
-chain
![]() $((e_n,p_n) \mid n)$
to
$((e_n,p_n) \mid n)$
to
![]() $\overline{X}$
. If
$\overline{X}$
. If
![]() $\overline{g}_n$
is the idempotent
$\overline{g}_n$
is the idempotent
![]() $\overline{f}_n\circ\overline{q}_n$
on
$\overline{f}_n\circ\overline{q}_n$
on
![]() $\overline{X}$
, then
$\overline{X}$
, then
![]() $(\overline{g}_n \mid n)$
is an
$(\overline{g}_n \mid n)$
is an
![]() $\omega$
-chain in
$\omega$
-chain in
![]() $\mathbb{I}(\overline{X})$
and is jointly monic in
$\mathbb{I}(\overline{X})$
and is jointly monic in
![]() $\mathbb{A}$
.
$\mathbb{A}$
.
Theorem 3.9 on the next page implies existence and uniqueness of
![]() $\iota:\underline{X} \to \overline{X}$
in
$\iota:\underline{X} \to \overline{X}$
in
![]() $\mathbb{A}$
such that
$\mathbb{A}$
such that
![]() $\forall n.\iota\circ\underline{f}_n=\overline{f}_n$
and
$\forall n.\iota\circ\underline{f}_n=\overline{f}_n$
and
![]() $\forall n.\underline{q}_n=\overline{q}_n\circ\iota$
, where
$\forall n.\underline{q}_n=\overline{q}_n\circ\iota$
, where
![]() $ ((\underline{f}_n,\underline{q}_n):X_n \to \underline{X} \mid n)$
and
$ ((\underline{f}_n,\underline{q}_n):X_n \to \underline{X} \mid n)$
and
![]() $((\overline{f}_n,\overline{q}_n):X_n \to \overline{X} \mid n)$
are the cones in
$((\overline{f}_n,\overline{q}_n):X_n \to \overline{X} \mid n)$
are the cones in
![]() $\mathbb{A}_{sr}$
given by Proposition 3.6 and Corollary 3.7. In general, there is no reason for
$\mathbb{A}_{sr}$
given by Proposition 3.6 and Corollary 3.7. In general, there is no reason for
![]() $\iota$
to be monic, epic, or iso, as demonstrated in the examples below.
$\iota$
to be monic, epic, or iso, as demonstrated in the examples below.
Example 3.8. We consider some examples of
![]() $\omega$
-chains
$\omega$
-chains
![]() $((e_n,p_n):X_n\to X_{n+1} \mid n \in \omega)$
in
$((e_n,p_n):X_n\to X_{n+1} \mid n \in \omega)$
in
![]() $\mathbb{A}_{sr}$
for several categories
$\mathbb{A}_{sr}$
for several categories
![]() $\mathbb{A}$
, in which the colimit cone of Proposition 3.6 and the limit cone of Corollary 3.7 exist. For each example, we give an explicit description of the colimit object
$\mathbb{A}$
, in which the colimit cone of Proposition 3.6 and the limit cone of Corollary 3.7 exist. For each example, we give an explicit description of the colimit object
![]() $\underline{X}$
and the limit object
$\underline{X}$
and the limit object
![]() $\overline{X}$
, and the properties of the unique map
$\overline{X}$
, and the properties of the unique map
![]() $\iota:\underline{X} \to \overline{X}$
in
$\iota:\underline{X} \to \overline{X}$
in
![]() $\mathbb{A}$
.
$\mathbb{A}$
.
-
We start with the category
 $\mathbf{CL}$
. In fact, the example is within the full sub-category
$\mathbf{CL}$
. In fact, the example is within the full sub-category
 $\omega\mathbf{CL}$
, whose objects are the retracts of
$\omega\mathbf{CL}$
, whose objects are the retracts of
 $\mathbb{P}(\omega)$
. Since
$\mathbb{P}(\omega)$
. Since
 $\mathbf{CL}$
is poset-enriched, one can ask whether a section is an embedding. Let
$\mathbf{CL}$
is poset-enriched, one can ask whether a section is an embedding. Let
 $X_n$
be the finite ordinal
$X_n$
be the finite ordinal
 $n+1$
and
$n+1$
and
 $e_n$
be the inclusion of
$e_n$
be the inclusion of
 $X_n$
into
$X_n$
into
 $X_{n+1}$
. There is only one possible retraction
$X_{n+1}$
. There is only one possible retraction
 $p_n$
for
$p_n$
for
 $e_n$
(because of monotonicity), which maps the largest element of
$e_n$
(because of monotonicity), which maps the largest element of
 $n+2$
—i.e.,
$n+2$
—i.e.,
 $n+1$
—to the largest element of
$n+1$
—to the largest element of
 $n+1$
—i.e., n—and is the identity otherwise. Moreover,
$n+1$
—i.e., n—and is the identity otherwise. Moreover,
 $(e_n,p_n)$
is an embedding-projection pair. Since in
$(e_n,p_n)$
is an embedding-projection pair. Since in
 $\mathbf{CL}$
the limit-colimit coincidence for
$\mathbf{CL}$
the limit-colimit coincidence for
 $\omega$
-chains of embedding-projection pairs holds, we have
$\omega$
-chains of embedding-projection pairs holds, we have
 $\underline{X}=\overline{X}=\omega+1$
and
$\underline{X}=\overline{X}=\omega+1$
and
 $\iota$
is an iso.
$\iota$
is an iso. -
Since the inclusion functor from
 $\mathbf{CL}$
to
$\mathbf{CL}$
to
 $\mathbf{Po}$
is poset-enriched, the
$\mathbf{Po}$
is poset-enriched, the
 $\omega$
-chain of embedding-projection pairs defined in the previous example is also an
$\omega$
-chain of embedding-projection pairs defined in the previous example is also an
 $\omega$
-chain of embedding-projection pairs in
$\omega$
-chain of embedding-projection pairs in
 $\mathbf{Po}$
. However, the limit-colimit coincidence does not hold in
$\mathbf{Po}$
. However, the limit-colimit coincidence does not hold in
 $\mathbf{Po}$
. In particular, in
$\mathbf{Po}$
. In particular, in
 $\mathbf{Po}$
we have
$\mathbf{Po}$
we have
 $\underline{X}=\omega$
,
$\underline{X}=\omega$
,
 $\overline{X}=\omega+1$
, and
$\overline{X}=\omega+1$
, and
 $\iota$
is the inclusion of
$\iota$
is the inclusion of
 $\omega$
into
$\omega$
into
 $\omega+1$
. Therefore,
$\omega+1$
. Therefore,
 $\iota$
is monic, but it is not epic (nor a section).
$\iota$
is monic, but it is not epic (nor a section). -
Since the forgetful functor from
 $\mathbf{Po}$
to
$\mathbf{Po}$
to
 $\mathbf{Set}$
is not poset-enriched, an
$\mathbf{Set}$
is not poset-enriched, an
 $\omega$
-chain of embedding-projection pairs in
$\omega$
-chain of embedding-projection pairs in
 $\mathbf{Po}$
becomes an
$\mathbf{Po}$
becomes an
 $\omega$
-chain of section-retraction pairs. However, the forgetful functor preserves limits and colimits. Thus, in
$\omega$
-chain of section-retraction pairs. However, the forgetful functor preserves limits and colimits. Thus, in
 $\mathbf{Set}$
, we have
$\mathbf{Set}$
, we have
 $\underline{X}=\omega$
,
$\underline{X}=\omega$
,
 $\overline{X}=\omega+1$
, and
$\overline{X}=\omega+1$
, and
 $\iota$
is the inclusion of
$\iota$
is the inclusion of
 $\omega$
into
$\omega$
into
 $\omega+1$
. In
$\omega+1$
. In
 $\mathbf{Set}$
, the map
$\mathbf{Set}$
, the map
 $\iota$
is monic (actually a section), but it is not epic.
$\iota$
is monic (actually a section), but it is not epic. -
The
 $\omega$
-chain of section-retraction pairs defined in
$\omega$
-chain of section-retraction pairs defined in
 $\mathbf{Set}$
can be viewed in the dual category
$\mathbf{Set}$
can be viewed in the dual category
 $\mathbf{Set}^{op}$
, by swapping the components of a pair. Therefore,
$\mathbf{Set}^{op}$
, by swapping the components of a pair. Therefore,
 $\iota$
in
$\iota$
in
 $\mathbf{Set}^{op}$
is epic (actually a retraction), but it is not monic.
$\mathbf{Set}^{op}$
is epic (actually a retraction), but it is not monic. -
The previous two examples can be combined in the product category
 $\mathbf{Set}\times\mathbf{Set}^{op}$
. In this case,
$\mathbf{Set}\times\mathbf{Set}^{op}$
. In this case,
 $\underline{X}$
is the pair
$\underline{X}$
is the pair
 $(\omega,\omega+1)$
,
$(\omega,\omega+1)$
,
 $\overline{X}$
is the pair
$\overline{X}$
is the pair
 $(\omega+1,\omega)$
, and
$(\omega+1,\omega)$
, and
 $\iota$
is neither epic nor monic.
$\iota$
is neither epic nor monic. -
The full&faithful functor D from
 $\mathbf{Set}$
to
$\mathbf{Set}$
to
 $\mathbf{Haus}$
(see Figure 1) preserve colimits. Thus, for the image of the
$\mathbf{Haus}$
(see Figure 1) preserve colimits. Thus, for the image of the
 $\omega$
-chain of section-retraction pairs in
$\omega$
-chain of section-retraction pairs in
 $\mathbf{Set}$
, we have
$\mathbf{Set}$
, we have
 $\underline{X}=D\omega$
,
$\underline{X}=D\omega$
,
 $\overline{X}$
is the one-point (aka Alexandroff) compactification of
$\overline{X}$
is the one-point (aka Alexandroff) compactification of
 $D\omega$
, whose carrier is
$D\omega$
, whose carrier is
 $\omega+1$
, and
$\omega+1$
, and
 $\iota$
is the inclusion of
$\iota$
is the inclusion of
 $\omega$
into
$\omega$
into
 $\omega+1$
. In
$\omega+1$
. In
 $\mathbf{Haus}$
, the map
$\mathbf{Haus}$
, the map
 $\iota$
is both monic and epic, since
$\iota$
is both monic and epic, since
 $\underline{X}$
is a dense sub-space of
$\underline{X}$
is a dense sub-space of
 $\overline{X}$
.
$\overline{X}$
.
If we start from an
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
in
$(g_n \mid n)$
in
![]() $\mathbb{I}(X)$
, where X is an object of interest in
$\mathbb{I}(X)$
, where X is an object of interest in
![]() $\mathbb{A}$
, then we can get, by splitting the idempotents, an
$\mathbb{A}$
, then we can get, by splitting the idempotents, an
![]() $\omega$
-chain in
$\omega$
-chain in
![]() $\mathbb{A}_{sr}$
which is unique up to iso. From this
$\mathbb{A}_{sr}$
which is unique up to iso. From this
![]() $\omega$
-chain, there are three cones in
$\omega$
-chain, there are three cones in
![]() $\mathbb{A}_{sr}$
, whose vertices are
$\mathbb{A}_{sr}$
, whose vertices are
![]() $\underline{X}$
, X and
$\underline{X}$
, X and
![]() $\overline{X}$
, respectively. The following theorem states that these cones are related by unique maps
$\overline{X}$
, respectively. The following theorem states that these cones are related by unique maps
![]() $\underline{\iota}:\underline{X}\to X$
and
$\underline{\iota}:\underline{X}\to X$
and
![]() $\overline{\iota}:X\to\overline{X}$
in
$\overline{\iota}:X\to\overline{X}$
in
![]() $\mathbb{A}$
. There is also an inverse (which we do not prove), where we start from an
$\mathbb{A}$
. There is also an inverse (which we do not prove), where we start from an
![]() $\omega$
-chain
$\omega$
-chain
![]() $((e_n,p_n) \mid n)$
in
$((e_n,p_n) \mid n)$
in
![]() $\mathbb{A}_{sr}$
, and consider the unique map
$\mathbb{A}_{sr}$
, and consider the unique map
![]() $\iota:\underline{X}\to\overline{X}$
in
$\iota:\underline{X}\to\overline{X}$
in
![]() $\mathbb{A}$
, relating the cones in
$\mathbb{A}$
, relating the cones in
![]() $\mathbb{A}_{sr}$
from the
$\mathbb{A}_{sr}$
from the
![]() $\omega$
-chain to
$\omega$
-chain to
![]() $\underline{X}$
and
$\underline{X}$
and
![]() $\overline{X}$
. In this case, any factorization
$\overline{X}$
. In this case, any factorization
![]() $(\underline{\iota},\overline{\iota})$
of
$(\underline{\iota},\overline{\iota})$
of
![]() $\iota$
through an object X, induces a
$\iota$
through an object X, induces a
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
of idempotents in
$(g_n \mid n)$
of idempotents in
![]() $\mathbb{I}(X)$
, where
$\mathbb{I}(X)$
, where
![]() $g_n=\underline{\iota}\circ\underline{f}_n\circ\overline{q}_n\circ\overline{\iota}$
.
$g_n=\underline{\iota}\circ\underline{f}_n\circ\overline{q}_n\circ\overline{\iota}$
.
Theorem 3.9.
If
![]() $(g_n \mid n)$
is an
$(g_n \mid n)$
is an
![]() $\omega$
-chain in
$\omega$
-chain in
![]() $\mathbb{I}(X)$
and every
$\mathbb{I}(X)$
and every
![]() $g_n$
has a splitting
$g_n$
has a splitting
![]() $(f_n,q_n):X_n \to X$
, then there exists a unique
$(f_n,q_n):X_n \to X$
, then there exists a unique
![]() $\omega$
-chain
$\omega$
-chain
![]() $((e_n,p_n):X_n \to X_{n+1} \mid n)$
in
$((e_n,p_n):X_n \to X_{n+1} \mid n)$
in
![]() $\mathbb{A}_{sr}$
such that
$\mathbb{A}_{sr}$
such that
![]() $((f_n,q_n):X_n\to X \mid n)$
is a cone in
$((f_n,q_n):X_n\to X \mid n)$
is a cone in
![]() $\mathbb{A}_{sr}$
from
$\mathbb{A}_{sr}$
from
![]() $((e_n,p_n):X_n\to X_{n+1} \mid n)$
to X. Moreover:
$((e_n,p_n):X_n\to X_{n+1} \mid n)$
to X. Moreover:
-
(1) If
 $(\underline{f}_n:X_n \to \underline{X} \mid n)$
is a colimit cone in
$(\underline{f}_n:X_n \to \underline{X} \mid n)$
is a colimit cone in
 $\mathbb{A}$
from the
$\mathbb{A}$
from the
 $\omega$
-chain
$\omega$
-chain
 $(e_n:X_n \to X_{n+1} \mid n)$
to
$(e_n:X_n \to X_{n+1} \mid n)$
to
 $\underline{X}$
and
$\underline{X}$
and
 $\underline{\iota}:\underline{X}\to X$
is the unique map such that
$\underline{\iota}:\underline{X}\to X$
is the unique map such that
 $\forall n.f_n=\underline{\iota}\circ\underline{f}_n$
, then
$\forall n.f_n=\underline{\iota}\circ\underline{f}_n$
, then
 $\forall n.q_n\circ\underline{\iota} = \underline{q}_n$
(see Proposition 3.6 for
$\forall n.q_n\circ\underline{\iota} = \underline{q}_n$
(see Proposition 3.6 for
 $\underline{q}_n$
).
$\underline{q}_n$
). -
(2) If
 $(\overline{q}_n:\overline{X}\to X_n \mid n)$
is a limit cone in
$(\overline{q}_n:\overline{X}\to X_n \mid n)$
is a limit cone in
 $\mathbb{A}$
from
$\mathbb{A}$
from
 $\overline{X}$
to the
$\overline{X}$
to the
 $\omega^{op}$
-chain
$\omega^{op}$
-chain
 $(p_n:X_{n+1}\to X_n \mid n)$
and
$(p_n:X_{n+1}\to X_n \mid n)$
and
 $\overline{\iota}:X\to \overline{X}$
is the unique map such that
$\overline{\iota}:X\to \overline{X}$
is the unique map such that
 $\forall n.q_n=\overline{q}_n\circ\overline{\iota}$
, then
$\forall n.q_n=\overline{q}_n\circ\overline{\iota}$
, then
 $\forall n.\overline{\iota}\circ f_n = \overline{f}_n$
(see Corollary 3.7 for
$\forall n.\overline{\iota}\circ f_n = \overline{f}_n$
(see Corollary 3.7 for
 $\overline{f}_n$
).
$\overline{f}_n$
).
Proof. By Item (5) of Proposition 3.5, we get that for each
![]() $n \in \omega$
there exists a unique sr-pair
$n \in \omega$
there exists a unique sr-pair
![]() $(e_n,p_n)$
such that
$(e_n,p_n)$
such that
![]() $(f_{n+1},q_{n+1})\circ(e_n,p_n)=(f_n,q_n)$
, which implies that
$(f_{n+1},q_{n+1})\circ(e_n,p_n)=(f_n,q_n)$
, which implies that
![]() $((f_n,q_n):X_n\to X \mid n)$
is a cone in
$((f_n,q_n):X_n\to X \mid n)$
is a cone in
![]() $\mathbb{A}_{sr}$
from the
$\mathbb{A}_{sr}$
from the
![]() $\omega$
-chain
$\omega$
-chain
![]() $((e_n,p_n):X_n\to X_{n+1} \mid n)$
to X.
$((e_n,p_n):X_n\to X_{n+1} \mid n)$
to X.
Item (1).
We rely on the proof of Proposition 3.6, where
![]() $\underline{q}_n$
is defined. Since
$\underline{q}_n$
is defined. Since
![]() $(\underline{f}_i \mid i)$
is jointly epic,
$(\underline{f}_i \mid i)$
is jointly epic,
![]() $\forall j.q_j\circ\underline{\iota} = \underline{q}_j$
follows from
$\forall j.q_j\circ\underline{\iota} = \underline{q}_j$
follows from
![]() $\forall i,j.q_j\circ\underline{\iota}\circ\underline{f}_i = \underline{q}_j\circ\underline{f}_i$
, or equivalently, from
$\forall i,j.q_j\circ\underline{\iota}\circ\underline{f}_i = \underline{q}_j\circ\underline{f}_i$
, or equivalently, from
![]() $\forall i,j.q_j\circ f_i = h_{i,j}$
, which we prove by induction on
$\forall i,j.q_j\circ f_i = h_{i,j}$
, which we prove by induction on
![]() $|j-i|$
:
$|j-i|$
:
-
case
 $i=j$
: immediate, since
$i=j$
: immediate, since
 $q_i\circ f_i=\text{id}_{X_i}=h_{i,i}$
, because
$q_i\circ f_i=\text{id}_{X_i}=h_{i,i}$
, because
 $(f_i,q_i)$
is a map in
$(f_i,q_i)$
is a map in
 $\mathbb{A}_{sr}$
and by definition of
$\mathbb{A}_{sr}$
and by definition of
 $h_{i,i}$
.
$h_{i,i}$
. -
case
 $i<j$
:
$i<j$
:-
 $q_j\circ f_i=$
because
$q_j\circ f_i=$
because
 $(f_{i+1},q_{i+1})\circ(e_i,p_i)=(f_i,q_i)$
in
$(f_{i+1},q_{i+1})\circ(e_i,p_i)=(f_i,q_i)$
in
 $\mathbb{A}_{sr}$
$\mathbb{A}_{sr}$
-
 $q_j\circ f_{i+1}\circ e_i=$
by IH on
$q_j\circ f_{i+1}\circ e_i=$
by IH on
 $(i+1,j)$
$(i+1,j)$
-
 $h_{i+1,j}\circ e_i=h_{i,j}$
by definition of
$h_{i+1,j}\circ e_i=h_{i,j}$
by definition of
 $h_{i,j}$
.
$h_{i,j}$
.
-
-
case
 $i>j$
:
$i>j$
:-
 $q_j\circ f_i=$
because
$q_j\circ f_i=$
because
 $(f_{i+1},q_{i+1})\circ(e_i,p_i)=(f_i,q_i)$
in
$(f_{i+1},q_{i+1})\circ(e_i,p_i)=(f_i,q_i)$
in
 $\mathbb{A}_{sr}$
$\mathbb{A}_{sr}$
-
 $p_j\circ q_{j+1}\circ f_i=$
by IH on
$p_j\circ q_{j+1}\circ f_i=$
by IH on
 $(i,j+1)$
$(i,j+1)$
-
 $p_j\circ h_{i,j+1}=h_{i,j}$
by definition of
$p_j\circ h_{i,j+1}=h_{i,j}$
by definition of
 $h_{i,j}$
.
$h_{i,j}$
.
-
3.2 Extended metric spaces versus compact Hausdorff spaces
The following result requires moving between four categories (and we have added also
![]() $\mathbf{Set}$
) using four functors (where
$\mathbf{Set}$
) using four functors (where
![]() denotes a faithful functor and
denotes a faithful functor and
![]() a full&faithful functor):2
a full&faithful functor):2

All the categories in the above diagram have:
-
finite limits and finite sums (Theorem 2.3);
-
enough points, more precisely, the faithful forgetful functor U from
 $\mathbb{A}$
into
$\mathbb{A}$
into
 $\mathbf{Set}$
is (isomorphic) to the global section functor
$\mathbf{Set}$
is (isomorphic) to the global section functor
 $\mathbb{A}(1,-)$
, where
$\mathbb{A}(1,-)$
, where
 $\mathbb{A}$
is any of the other four categories (
$\mathbb{A}$
is any of the other four categories (
 $\mathbf{KMS}$
,
$\mathbf{KMS}$
,
 $\mathbf{Met}$
,
$\mathbf{Met}$
,
 $\mathbf{KH}$
or
$\mathbf{KH}$
or
 $\mathbf{Haus}$
), and 1 is the terminal object in
$\mathbf{Haus}$
), and 1 is the terminal object in
 $\mathbb{A}$
;
$\mathbb{A}$
; -
splittings of idempotents, because each of the five categories has equalizers.
Moreover, all functors in the diagrams preserve finite limits and finite sums;
![]() $\mathbf{Haus}$
has all small limits and small colimits (Theorem 2.4), where limits are computed as in
$\mathbf{Haus}$
has all small limits and small colimits (Theorem 2.4), where limits are computed as in
![]() $\mathbf{Top}$
, and limits (computed in
$\mathbf{Top}$
, and limits (computed in
![]() $\mathbf{Haus}$
) of diagrams in
$\mathbf{Haus}$
) of diagrams in
![]() $\mathbf{KH}$
are in
$\mathbf{KH}$
are in
![]() $\mathbf{KH}$
.
$\mathbf{KH}$
.
In applications, we start from a metric space
![]() $\mathbb{S}$
, then we identify an
$\mathbb{S}$
, then we identify an
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
of idempotents on
$(g_n \mid n)$
of idempotents on
![]() $\mathbb{S}$
in
$\mathbb{S}$
in
![]() $\mathbf{Met}$
, and by applying Theorem 3.9 in
$\mathbf{Met}$
, and by applying Theorem 3.9 in
![]() $\mathbf{Haus,}$
we get a map
$\mathbf{Haus,}$
we get a map
![]() $\overline{\iota}:\mathbb{S}\to\overline{\mathbb{S}}$
in
$\overline{\iota}:\mathbb{S}\to\overline{\mathbb{S}}$
in
![]() $\mathbf{Haus}$
. The theorems below provide sufficient conditions to ensure that
$\mathbf{Haus}$
. The theorems below provide sufficient conditions to ensure that
![]() $\overline{\mathbb{S}}$
is compact,
$\overline{\mathbb{S}}$
is compact,
![]() $\overline{\iota}$
is monic and epic, and, above all, that the complete lattice
$\overline{\iota}$
is monic and epic, and, above all, that the complete lattice
![]() $\mathbb{C}(\overline{\mathbb{S}})$
is
$\mathbb{C}(\overline{\mathbb{S}})$
is
![]() $\omega$
-continuous and the monotonic map
$\omega$
-continuous and the monotonic map
![]() $\mathbb{C}(\overline{\iota})$
is in
$\mathbb{C}(\overline{\iota})$
is in
![]() $\mathbb{A}_{RS}(\mathbb{S},\overline{\mathbb{S}})$
. These properties can be proved for maps
$\mathbb{A}_{RS}(\mathbb{S},\overline{\mathbb{S}})$
. These properties can be proved for maps
![]() $\iota\,:\,\mathbb{S}\to\overline{\mathbb{S}}$
that are not necessarily obtained through Theorem 3.9, and the theorems below capture this greater generality. If we start from an
$\iota\,:\,\mathbb{S}\to\overline{\mathbb{S}}$
that are not necessarily obtained through Theorem 3.9, and the theorems below capture this greater generality. If we start from an
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
of idempotents on
$(g_n \mid n)$
of idempotents on
![]() $\mathbb{S}$
in
$\mathbb{S}$
in
![]() $\mathbf{Met}$
, then Theorem 3.9 provides candidates for
$\mathbf{Met}$
, then Theorem 3.9 provides candidates for
![]() $(p_n \mid n)$
and
$(p_n \mid n)$
and
![]() $(q_n \mid n)$
in the following theorem, because
$(q_n \mid n)$
in the following theorem, because
![]() $\mathbf{Met}$
has splittings of idempotents.
$\mathbf{Met}$
has splittings of idempotents.
Theorem 3.10.
If
![]() $(p_n:\mathbb{S}_{n+1}\to \mathbb{S}_n \mid n)$
is an
$(p_n:\mathbb{S}_{n+1}\to \mathbb{S}_n \mid n)$
is an
![]() $\omega^{op}$
-chain in
$\omega^{op}$
-chain in
![]() $\mathbf{KMS}$
,
$\mathbf{KMS}$
,
![]() $(q_n \mid n)$
is a cone from
$(q_n \mid n)$
is a cone from
![]() $\mathbb{S}$
to
$\mathbb{S}$
to
![]() $(p_n \mid n)$
in
$(p_n \mid n)$
in
![]() $\mathbf{Met}$
,
$\mathbf{Met}$
,
![]() $(\overline{q}_n:\overline{\mathbb{S}}\to \mathbb{S}_n \mid n)$
is a limit cone from
$(\overline{q}_n:\overline{\mathbb{S}}\to \mathbb{S}_n \mid n)$
is a limit cone from
![]() $\overline{\mathbb{S}}$
to
$\overline{\mathbb{S}}$
to
![]() $(p_n \mid n)$
in
$(p_n \mid n)$
in
![]() $\mathbf{KH}$
(and
$\mathbf{KH}$
(and
![]() $\mathbf{Haus}$
), and
$\mathbf{Haus}$
), and
![]() $\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
is the unique map in
$\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
is the unique map in
![]() $\mathbf{Haus}$
such that
$\mathbf{Haus}$
such that
![]() $q_n=\overline{q}_n\circ \iota$
(see Figure 4
), then:
$q_n=\overline{q}_n\circ \iota$
(see Figure 4
), then:
-
(1)
 $\overline{\mathbb{S}}$
is compact and has a countable base. Thus,
$\overline{\mathbb{S}}$
is compact and has a countable base. Thus,
 $\mathbb{C}(\overline{\mathbb{S}})$
is
$\mathbb{C}(\overline{\mathbb{S}})$
is
 $\omega$
-continuous.
$\omega$
-continuous. -
(2) The monotonic map
 $\mathbb{C}(\iota)$
is in
$\mathbb{C}(\iota)$
is in
 $\mathbb{A}_{RS}(\mathbb{S},\overline{\mathbb{S}})$
.
$\mathbb{A}_{RS}(\mathbb{S},\overline{\mathbb{S}})$
.

Figure 4. Partial diagrammatic recast of Theorem 3.10.
Proof. The Hausdorff space
![]() $\overline{\mathbb{S}}$
can be identified with the set
$\overline{\mathbb{S}}$
can be identified with the set
![]() $\{s \in \prod_n\lvert\thinspace {\mathbb{S}_n} \thinspace\rvert \mid \forall n. s_n=p_n(s_{n+1})\}$
, equipped with the coarsest topology
$\{s \in \prod_n\lvert\thinspace {\mathbb{S}_n} \thinspace\rvert \mid \forall n. s_n=p_n(s_{n+1})\}$
, equipped with the coarsest topology
![]() $\mathsf{O}(\overline{\mathbb{S}})$
making the maps
$\mathsf{O}(\overline{\mathbb{S}})$
making the maps
![]() $\overline{q}_n(s)=s_n$
continuous, i.e., the topology generated by the sub-base
$\overline{q}_n(s)=s_n$
continuous, i.e., the topology generated by the sub-base
![]() $[O]_n=\{s \in \lvert\thinspace {\overline{\mathbb{S}}} \thinspace\rvert \mid \overline{q}_n(s)\in O\}$
, where O is an open set in
$[O]_n=\{s \in \lvert\thinspace {\overline{\mathbb{S}}} \thinspace\rvert \mid \overline{q}_n(s)\in O\}$
, where O is an open set in
![]() $\mathbb{S}_n$
.
$\mathbb{S}_n$
.
By Theorem 2.4, the limit
![]() $\overline{\mathbb{S}}$
is in
$\overline{\mathbb{S}}$
is in
![]() $\mathbf{KH}$
, because it is the limit (in
$\mathbf{KH}$
, because it is the limit (in
![]() $\mathbf{Haus}$
) of a diagram in
$\mathbf{Haus}$
) of a diagram in
![]() $\mathbf{KH}$
. The topology on
$\mathbf{KH}$
. The topology on
![]() $\mathbb{S}_n$
has a countable base
$\mathbb{S}_n$
has a countable base
![]() $\tau^b_n$
, because
$\tau^b_n$
, because
![]() $\mathbb{S}_n$
is in
$\mathbb{S}_n$
is in
![]() $\mathbf{KMS}$
. Thus, the topology on
$\mathbf{KMS}$
. Thus, the topology on
![]() $\overline{\mathbb{S}}$
has a countable sub-base too, namely the set of open subsets of the form
$\overline{\mathbb{S}}$
has a countable sub-base too, namely the set of open subsets of the form
![]() $[B]_n$
with
$[B]_n$
with
![]() $B\in\tau^b_n$
.
$B\in\tau^b_n$
.
By Theorem 2.27, the complete lattice
![]() $\mathbb{C}(X)$
is in
$\mathbb{C}(X)$
is in
![]() $\mathbf{CL}$
and the topologies
$\mathbf{CL}$
and the topologies
![]() $\tau_S(X)$
and
$\tau_S(X)$
and
![]() $\tau_U(X)$
coincide, when
$\tau_U(X)$
coincide, when
![]() $X:\mathbf{KH}$
, as in the case of
$X:\mathbf{KH}$
, as in the case of
![]() $\mathbb{S}_n$
and
$\mathbb{S}_n$
and
![]() $\overline{\mathbb{S}}$
. Therefore,
$\overline{\mathbb{S}}$
. Therefore,
![]() $\tau_S(X)$
is generated by
$\tau_S(X)$
is generated by
![]() $\uparrow O\stackrel{\triangle}{=}\{K \in \mathsf{C}(X) \mid K\subseteq O\}$
with
$\uparrow O\stackrel{\triangle}{=}\{K \in \mathsf{C}(X) \mid K\subseteq O\}$
with
![]() $O \in \mathsf{O}(X)$
, and the way-below relation is given by
$O \in \mathsf{O}(X)$
, and the way-below relation is given by
![]() $K_1\ll K_2\iff K_2\subseteq {{{K_1}^{\circ}}}$
, where
$K_1\ll K_2\iff K_2\subseteq {{{K_1}^{\circ}}}$
, where
![]() ${{{K_1}^{\circ}}}$
is the interior of
${{{K_1}^{\circ}}}$
is the interior of
![]() $K_1$
.
$K_1$
.
By Theorem 2.32, the continuous lattice
![]() $\mathbb{C}(\overline{\mathbb{S}})$
is (isomorphic to) the limit of the
$\mathbb{C}(\overline{\mathbb{S}})$
is (isomorphic to) the limit of the
![]() $\omega^{op}$
-chain of right adjoints
$\omega^{op}$
-chain of right adjoints
![]() $(\mathbb{C}(p_n) \mid n)$
in
$(\mathbb{C}(p_n) \mid n)$
in
![]() $\mathbf{CL}$
(and in
$\mathbf{CL}$
(and in
![]() $\mathbf{Po}_A$
). To be more precise, the iso is
$\mathbf{Po}_A$
). To be more precise, the iso is
![]() $K\mapsto(\overline{q}_n(K) \mid n)$
with inverse
$K\mapsto(\overline{q}_n(K) \mid n)$
with inverse
![]() $(K_n \mid n)\mapsto\bigcap_n \overline{q}_n^*(K_n)$
.
$(K_n \mid n)\mapsto\bigcap_n \overline{q}_n^*(K_n)$
.
The sub-base of
![]() $\mathsf{O}(\overline{\mathbb{S}})$
given above, i.e., the set of
$\mathsf{O}(\overline{\mathbb{S}})$
given above, i.e., the set of
![]() $[O]_n=\{s \in \lvert\thinspace {\overline{\mathbb{S}}} \thinspace\rvert \mid \overline{q}_n(s)\in O\}$
, where O is an open set in
$[O]_n=\{s \in \lvert\thinspace {\overline{\mathbb{S}}} \thinspace\rvert \mid \overline{q}_n(s)\in O\}$
, where O is an open set in
![]() $\mathbb{S}_n$
, is actually a base, because
$\mathbb{S}_n$
, is actually a base, because
![]() $[O]_n=[p_n^*(O)]_{n+1}$
. Therefore, every
$[O]_n=[p_n^*(O)]_{n+1}$
. Therefore, every
![]() $O \in \mathsf{O}(\overline{\mathbb{S}})$
is of the form
$O \in \mathsf{O}(\overline{\mathbb{S}})$
is of the form
![]() $\bigcup_{i \in I}[O_i]_{n_i}$
with
$\bigcup_{i \in I}[O_i]_{n_i}$
with
![]() $O_i \in \mathsf{O}(\mathbb{S}_{n_i})$
for
$O_i \in \mathsf{O}(\mathbb{S}_{n_i})$
for
![]() $i \in I$
. Since
$i \in I$
. Since
![]() $\overline{\mathbb{S}}$
is compact, also
$\overline{\mathbb{S}}$
is compact, also
![]() $K \in \mathsf{C}(\overline{\mathbb{S}})$
is compact, and
$K \in \mathsf{C}(\overline{\mathbb{S}})$
is compact, and
![]() $K\subseteq O$
implies
$K\subseteq O$
implies
![]() $K\subseteq\bigcup_{i \in J}[O_i]_{n_i}$
for some
$K\subseteq\bigcup_{i \in J}[O_i]_{n_i}$
for some
![]() $J\subseteq_f I$
. In particular,
$J\subseteq_f I$
. In particular,
![]() $O\supseteq\bigcup_{i \in J}[O_i]_{n_i}=[O_J]_{n_J}$
, where
$O\supseteq\bigcup_{i \in J}[O_i]_{n_i}=[O_J]_{n_J}$
, where
![]() $n_J=\sup_{i \in J} n_i$
and
$n_J=\sup_{i \in J} n_i$
and
![]() $O_J \in \mathsf{O}(\mathbb{S}_{n_J})$
is the union for
$O_J \in \mathsf{O}(\mathbb{S}_{n_J})$
is the union for
![]() $i \in J$
of the
$i \in J$
of the
![]() $O_i$
moved from
$O_i$
moved from
![]() $\mathbb{S}_{n_i}$
to
$\mathbb{S}_{n_i}$
to
![]() $\mathbb{S}_{n_J}$
. Therefore:
$\mathbb{S}_{n_J}$
. Therefore:
Using the above property, and
![]() $\delta$
-fattening (see Definition 2.5), we have:
$\delta$
-fattening (see Definition 2.5), we have:
-
 $\mathbb{C}(\iota):\mathbb{A}_{RS}(\mathbb{S},\overline{\mathbb{S}})$
means
$\mathbb{C}(\iota):\mathbb{A}_{RS}(\mathbb{S},\overline{\mathbb{S}})$
means
 $\forall C \in \mathsf{C}(\mathbb{S}).\forall O \in \mathsf{O}(\overline{\mathbb{S}}).\overline{\iota(C)}\subseteq O\implies\exists\delta>0.\overline{\iota(C_\delta)}\subseteq O$
, in which
$\forall C \in \mathsf{C}(\mathbb{S}).\forall O \in \mathsf{O}(\overline{\mathbb{S}}).\overline{\iota(C)}\subseteq O\implies\exists\delta>0.\overline{\iota(C_\delta)}\subseteq O$
, in which
 $C_\delta$
is as defined in item (3) of Definition 2.5.
$C_\delta$
is as defined in item (3) of Definition 2.5. -
By property (2), this is implied by
 \begin{align*} \forall C \in \mathsf{C}(\mathbb{S}).\forall n.\forall O \in \mathsf{O}(\mathbb{S}_n).\overline{\iota(C)}\subseteq [O]_n\implies\exists\delta>0.\overline{\iota(C_\delta)}\subseteq [O]_n \end{align*}
\begin{align*} \forall C \in \mathsf{C}(\mathbb{S}).\forall n.\forall O \in \mathsf{O}(\mathbb{S}_n).\overline{\iota(C)}\subseteq [O]_n\implies\exists\delta>0.\overline{\iota(C_\delta)}\subseteq [O]_n \end{align*}
-
which is equivalent to
because \begin{align*} \forall C \in \mathsf{C}(\mathbb{S}).\forall n.\forall O \in \mathsf{O}(\mathbb{S}_n).\overline{q_n(C)}\subseteq O\implies\exists\delta>0.\overline{q_n(C_\delta)}\subseteq O \end{align*}
\begin{align*} \forall C \in \mathsf{C}(\mathbb{S}).\forall n.\forall O \in \mathsf{O}(\mathbb{S}_n).\overline{q_n(C)}\subseteq O\implies\exists\delta>0.\overline{q_n(C_\delta)}\subseteq O \end{align*}
 $\overline{\iota(C)}\subseteq [O]_n\iff \overline{q}_n(\overline{\iota(C)}) \subseteq O$
, by definition of
$\overline{\iota(C)}\subseteq [O]_n\iff \overline{q}_n(\overline{\iota(C)}) \subseteq O$
, by definition of
 $[O]_n$
, and
$[O]_n$
, and
![]() $\overline{q}_n(\overline{\iota(C)})=\overline{\overline{q}_n(\overline{\iota(C)})}= \overline{q_n(C)}$
, by
$\overline{q}_n(\overline{\iota(C)})=\overline{\overline{q}_n(\overline{\iota(C)})}= \overline{q_n(C)}$
, by
![]() $q_n=\overline{q}_n\circ \iota$
and compactness of
$q_n=\overline{q}_n\circ \iota$
and compactness of
![]() $\overline{\iota(C)}$
.
$\overline{\iota(C)}$
.
Since
![]() $q_n:\mathbf{Met}(\mathbb{S},\mathbb{S}_n)$
and
$q_n:\mathbf{Met}(\mathbb{S},\mathbb{S}_n)$
and
![]() $\mathbb{S}_n:\mathbf{KMS}$
, by applying Proposition 2.7 to
$\mathbb{S}_n:\mathbf{KMS}$
, by applying Proposition 2.7 to
![]() $q_n$
and Proposition 2.8 to
$q_n$
and Proposition 2.8 to
![]() $\mathbb{S}_n$
, we get the chain of implications
$\mathbb{S}_n$
, we get the chain of implications
![]() $\overline{q_n(C)}\subseteq O\implies\exists\delta>0.\overline{q_n(C)}_\delta\subseteq O\implies\exists\delta>0.\overline{q_n(C_\delta)}\subseteq O$
for
$\overline{q_n(C)}\subseteq O\implies\exists\delta>0.\overline{q_n(C)}_\delta\subseteq O\implies\exists\delta>0.\overline{q_n(C_\delta)}\subseteq O$
for
![]() $C \in \mathsf{C}(\mathbb{S})$
and
$C \in \mathsf{C}(\mathbb{S})$
and
![]() $O \in \mathsf{O}(\mathbb{S}_n)$
.
$O \in \mathsf{O}(\mathbb{S}_n)$
.
If we start from an
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
of idempotents on
$(g_n \mid n)$
of idempotents on
![]() $\mathbb{S}$
in
$\mathbb{S}$
in
![]() $\mathbf{Met}$
, rather than in
$\mathbf{Met}$
, rather than in
![]() $\mathbf{Haus}$
, then
$\mathbf{Haus}$
, then
![]() $((f_n,q_n) \mid n)$
and
$((f_n,q_n) \mid n)$
and
![]() $((e_n,p_n) \mid n)$
in the following theorem consist of short maps. Moreover, families of maps that are jointly monic in
$((e_n,p_n) \mid n)$
in the following theorem consist of short maps. Moreover, families of maps that are jointly monic in
![]() $\mathbf{Met}$
are also jointly monic in
$\mathbf{Met}$
are also jointly monic in
![]() $\mathbf{Haus}$
, because these categories have enough points. Finally, by Proposition 3.5, if an
$\mathbf{Haus}$
, because these categories have enough points. Finally, by Proposition 3.5, if an
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
of idempotents on
$(g_n \mid n)$
of idempotents on
![]() $\mathbb{S}$
is jointly monic, then the identity on
$\mathbb{S}$
is jointly monic, then the identity on
![]() $\mathbb{S}$
is the sup of the
$\mathbb{S}$
is the sup of the
![]() $\omega$
-chain in the poset of idempotents on
$\omega$
-chain in the poset of idempotents on
![]() $\mathbb{S}$
.
$\mathbb{S}$
.
Theorem 3.11.
Given an
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
of idempotents on
$(g_n \mid n)$
of idempotents on
![]() $\mathbb{S}$
in
$\mathbb{S}$
in
![]() $\mathbf{Haus}$
, which is jointly monic, consider:
$\mathbf{Haus}$
, which is jointly monic, consider:
-
a splitting
 of
of
 $g_n$
;
$g_n$
; -
the unique
 $\omega$
-chain
$\omega$
-chain
 $((e_n,p_n):\mathbb{S}_n \to \mathbb{S}_{n+1} \mid n)$
in
$((e_n,p_n):\mathbb{S}_n \to \mathbb{S}_{n+1} \mid n)$
in
 $\mathbf{Haus}_{sr}$
such that
$\mathbf{Haus}_{sr}$
such that
 $((f_n,q_n):\mathbb{S}_n\to \mathbb{S} \mid n)$
is a cone in
$((f_n,q_n):\mathbb{S}_n\to \mathbb{S} \mid n)$
is a cone in
 $\mathbf{Haus}_{sr}$
from
$\mathbf{Haus}_{sr}$
from
 $((e_n,p_n):\mathbb{S}_n \to \mathbb{S}_{n+1} \mid n)$
to
$((e_n,p_n):\mathbb{S}_n \to \mathbb{S}_{n+1} \mid n)$
to
 $\mathbb{S}$
(see Theorem 3.9);
$\mathbb{S}$
(see Theorem 3.9);
-
the limit cone
 $(\overline{q}_n:\overline{\mathbb{S}}\to \mathbb{S}_n \mid n)$
in
$(\overline{q}_n:\overline{\mathbb{S}}\to \mathbb{S}_n \mid n)$
in
 $\mathbf{Haus}$
from
$\mathbf{Haus}$
from
 $\overline{\mathbb{S}}$
to the
$\overline{\mathbb{S}}$
to the
 $\omega^{op}$
-chain
$\omega^{op}$
-chain
 $(p_n:\mathbb{S}_{n+1}\to \mathbb{S}_n \mid n)$
;
$(p_n:\mathbb{S}_{n+1}\to \mathbb{S}_n \mid n)$
; -
the unique map
 $\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
in
$\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
in
 $\mathbf{Haus}$
such that
$\mathbf{Haus}$
such that
 $\forall n.q_n=\overline{q}_n\circ \iota$
.
$\forall n.q_n=\overline{q}_n\circ \iota$
.
Then,
![]() $\iota$
is both monic and epic in
$\iota$
is both monic and epic in
![]() $\mathbf{Haus}$
.
$\mathbf{Haus}$
.
Proof. If
![]() $(g_n \mid n)$
is jointly monic, then also
$(g_n \mid n)$
is jointly monic, then also
![]() $(q_n \mid n)$
is jointly monic, by (the dual of) Proposition 3.4, and
$(q_n \mid n)$
is jointly monic, by (the dual of) Proposition 3.4, and
![]() $\iota$
is monic, for the same reason.
$\iota$
is monic, for the same reason.
If
![]() $((\overline{f}_n,\overline{q}_n):\mathbb{S}_n\to \overline{\mathbb{S}} \mid n)$
is the unique cone in
$((\overline{f}_n,\overline{q}_n):\mathbb{S}_n\to \overline{\mathbb{S}} \mid n)$
is the unique cone in
![]() $\mathbf{Haus}_{sr}$
given by Corollary 3.7, then
$\mathbf{Haus}_{sr}$
given by Corollary 3.7, then
![]() $\forall n.\iota\circ f_n = \overline{f}_n$
, by Theorem 3.9. Therefore, to prove that
$\forall n.\iota\circ f_n = \overline{f}_n$
, by Theorem 3.9. Therefore, to prove that
![]() $\iota$
is epic it suffices, by Proposition 3.4, to prove that
$\iota$
is epic it suffices, by Proposition 3.4, to prove that
![]() $(\overline{f}_n \mid n)$
is jointly epic in
$(\overline{f}_n \mid n)$
is jointly epic in
![]() $\mathbf{Haus}$
. This amounts to proving that the union of the images of the maps in
$\mathbf{Haus}$
. This amounts to proving that the union of the images of the maps in
![]() $(\overline{f}_n \mid n)$
is dense in
$(\overline{f}_n \mid n)$
is dense in
![]() $\overline{\mathbb{S}}$
. To do this we use the base of
$\overline{\mathbb{S}}$
. To do this we use the base of
![]() $\mathsf{O}(\overline{\mathbb{S}})$
as in the proof of Theorem 3.10. For every
$\mathsf{O}(\overline{\mathbb{S}})$
as in the proof of Theorem 3.10. For every
![]() $s \in \overline{\mathbb{S}}$
and
$s \in \overline{\mathbb{S}}$
and
![]() $[O]_n$
in the base (i.e.,
$[O]_n$
in the base (i.e.,
![]() $O \in \mathsf{O}(\mathbb{S}_n)$
) such that
$O \in \mathsf{O}(\mathbb{S}_n)$
) such that
![]() $s \in [O]_n$
(i.e.,
$s \in [O]_n$
(i.e.,
![]() $\overline{q}_n(s) \in O$
), we have to give an
$\overline{q}_n(s) \in O$
), we have to give an
![]() $s_n \in \mathbb{S}_n$
such that
$s_n \in \mathbb{S}_n$
such that
![]() $\overline{f}_n(s_n) \in [O]_n$
. It suffice to take
$\overline{f}_n(s_n) \in [O]_n$
. It suffice to take
![]() $s_n=\overline{q}_n(s)$
, since
$s_n=\overline{q}_n(s)$
, since
![]() $s_n=\overline{q}_n(\overline{f}_n(s_n))$
.
$s_n=\overline{q}_n(\overline{f}_n(s_n))$
.
4. Examples
In this section, we consider examples of Banach spaces
![]() $\mathbb{S}$
, demonstrating how to apply the results of Section 3 to define a specific
$\mathbb{S}$
, demonstrating how to apply the results of Section 3 to define a specific
![]() $\overline{\mathbb{S}}$
in
$\overline{\mathbb{S}}$
in
![]() $\mathbf{KH}$
, and in which cases
$\mathbf{KH}$
, and in which cases
![]() $\overline{\mathbb{S}}$
is a compactification of
$\overline{\mathbb{S}}$
is a compactification of
![]() $\mathbb{S}$
(a summary is given at the end of this section, see Figure 5). In Section 5, we will study loss of precision when going from
$\mathbb{S}$
(a summary is given at the end of this section, see Figure 5). In Section 5, we will study loss of precision when going from
![]() $\mathbb{S}$
to
$\mathbb{S}$
to
![]() $\overline{\mathbb{S}}$
. All examples considered in this section are sequence spaces. Hence, we recall some general definitions and fix notation.
$\overline{\mathbb{S}}$
. All examples considered in this section are sequence spaces. Hence, we recall some general definitions and fix notation.

Figure 5. Summary of Examples of Section 4.
Definition 4.1. (Uniform notation). We write
![]() $\mathbb{R}$
for the standard Banach space on the reals, and also for the underlying vector space, metric space, topological space, and set:
$\mathbb{R}$
for the standard Banach space on the reals, and also for the underlying vector space, metric space, topological space, and set:
-
Given a set I, we write
 $\mathbb{R}^I$
for the product of I copies of the set
$\mathbb{R}^I$
for the product of I copies of the set
 $\mathbb{R}$
, which is also the carrier of the product of I copies of
$\mathbb{R}$
, which is also the carrier of the product of I copies of
 $\mathbb{R}$
in the categories of the vector spaces, extended metric spaces and Hausdorff spaces.
$\mathbb{R}$
in the categories of the vector spaces, extended metric spaces and Hausdorff spaces. -
Given a real number p in the interval
 $[1,\infty)$
, we write
$[1,\infty)$
, we write
 ${{{\lVert\thinspace {-}\thinspace\rVert}}}_{I,p}$
for the map from
${{{\lVert\thinspace {-}\thinspace\rVert}}}_{I,p}$
for the map from
 $\mathbb{R}^I$
to
$\mathbb{R}^I$
to
 $[0,\infty]$
given by
$[0,\infty]$
given by
 ${{{\lVert\thinspace {x}\,\rVert}}}_{I,p}\stackrel{\triangle}{=}(\sum_{i \in I}\lvert\, {x_i} \thinspace\rvert^p)^{1/p}$
, and the notation is extended to
${{{\lVert\thinspace {x}\,\rVert}}}_{I,p}\stackrel{\triangle}{=}(\sum_{i \in I}\lvert\, {x_i} \thinspace\rvert^p)^{1/p}$
, and the notation is extended to
 $p=\infty$
by defining
$p=\infty$
by defining
 ${{{\lVert\thinspace {x}\thinspace\rVert}}}_{I,\infty}\stackrel{\triangle}{=}\sup_{i \in I}\lvert\thinspace {x_i} \thinspace\rvert$
. Since I is determined by x, we drop the subscript I and write
${{{\lVert\thinspace {x}\thinspace\rVert}}}_{I,\infty}\stackrel{\triangle}{=}\sup_{i \in I}\lvert\thinspace {x_i} \thinspace\rvert$
. Since I is determined by x, we drop the subscript I and write
 ${{{\lVert\thinspace {x}\thinspace\rVert}}}_p$
.
${{{\lVert\thinspace {x}\thinspace\rVert}}}_p$
. -
We write
 $\ell_{I,p}$
for the Banach space with carrier the sub-space
$\ell_{I,p}$
for the Banach space with carrier the sub-space
 $\{x \in \mathbb{R}^I \mid {{{\lVert\thinspace {x}\thinspace\rVert}}}_p<\infty\}$
of (the vector space)
$\{x \in \mathbb{R}^I \mid {{{\lVert\thinspace {x}\thinspace\rVert}}}_p<\infty\}$
of (the vector space)
 $\mathbb{R}^I$
and norm
$\mathbb{R}^I$
and norm
 ${{{\lVert\thinspace {-}\thinspace\rVert}}}_{I,p}$
. We write
${{{\lVert\thinspace {-}\thinspace\rVert}}}_{I,p}$
. We write
 $B_{I,p}$
for the closed unit ball in
$B_{I,p}$
for the closed unit ball in
 $\ell_{I,p}$
, whose elements are those x such that
$\ell_{I,p}$
, whose elements are those x such that
 ${{{\lVert\thinspace {x}\thinspace\rVert}}}_p\leq 1$
. The subset
${{{\lVert\thinspace {x}\thinspace\rVert}}}_p\leq 1$
. The subset
 $B_{I,p}$
inherits from
$B_{I,p}$
inherits from
 $\ell_{I,p}$
the metric.
$\ell_{I,p}$
the metric. -
If
 $I\subseteq J$
, then
$I\subseteq J$
, then
 $\ell_{I,p}$
is isomorphic (in the category of Banach spaces and short linear maps) to the sub-space of
$\ell_{I,p}$
is isomorphic (in the category of Banach spaces and short linear maps) to the sub-space of
 $\ell_{J,p}$
with carrier
$\ell_{J,p}$
with carrier
 $\{x \mid \forall j \in J \setminus I.x_j=0\}$
, and
$\{x \mid \forall j \in J \setminus I.x_j=0\}$
, and
 $B_{I,p}$
is a sub-space of
$B_{I,p}$
is a sub-space of
 $B_{J,p}$
(modulo this iso).
$B_{J,p}$
(modulo this iso).
We consider only countable I, specifically, either
![]() $\omega$
or a natural number m. We write
$\omega$
or a natural number m. We write
![]() $\ell_{p}$
for
$\ell_{p}$
for
![]() $\ell_{\omega,p}$
and
$\ell_{\omega,p}$
and
![]() $\ell_{*,p}$
for the (normed vector) sub-space of
$\ell_{*,p}$
for the (normed vector) sub-space of
![]() $\ell_{p}$
with carrier
$\ell_{p}$
with carrier
![]() $\{x \mid \exists n.\forall i>n.x_i=0\}$
. We write
$\{x \mid \exists n.\forall i>n.x_i=0\}$
. We write
![]() $B_{p}$
for
$B_{p}$
for
![]() $B_{\omega,p}$
, and
$B_{\omega,p}$
, and
![]() $B_{*,p}$
for
$B_{*,p}$
for
![]() $B_{p}\cap\ell_{*,p}$
. Note that
$B_{p}\cap\ell_{*,p}$
. Note that
![]() $\ell_{0,p}$
is trivial and
$\ell_{0,p}$
is trivial and
![]() $\ell_{1,p}=\mathbb{R}$
for every p.
$\ell_{1,p}=\mathbb{R}$
for every p.
In the sequel, we use the following characterization of limits in
![]() $\mathbf{Top}$
and general properties of limits and colimits (valid in any category).
$\mathbf{Top}$
and general properties of limits and colimits (valid in any category).
Proposition 4.2.
Given a small diagram
![]() $D:I\to \mathbf{Top}$
, a limit cone
$D:I\to \mathbf{Top}$
, a limit cone
![]() $(\pi_i:(X,\tau)\to D_i \mid i \in I)$
in
$(\pi_i:(X,\tau)\to D_i \mid i \in I)$
in
![]() $\mathbf{Top}$
is obtained by taking a limit cone
$\mathbf{Top}$
is obtained by taking a limit cone
![]() $(\pi_i:X\to U(D_i) \mid i \in I)$
of
$(\pi_i:X\to U(D_i) \mid i \in I)$
of
![]() $U\circ D:I\to \mathbf{Set}$
in
$U\circ D:I\to \mathbf{Set}$
in
![]() $\mathbf{Set}$
, and by defining
$\mathbf{Set}$
, and by defining
![]() $\tau$
as the coarsest topology on X making the maps
$\tau$
as the coarsest topology on X making the maps
![]() $\pi_i:(X,\tau)\to D_i$
continuous.
$\pi_i:(X,\tau)\to D_i$
continuous.
Proposition 4.3. (Limits commute with Limits). Given an
![]() $I \times J$
-diagram
$I \times J$
-diagram
![]() $D:I \times J\to \mathbb{A}$
in a category
$D:I \times J\to \mathbb{A}$
in a category
![]() $\mathbb{A}$
(with the relevant limits), if for each
$\mathbb{A}$
(with the relevant limits), if for each
![]() $i \in I$
,
$i \in I$
,
![]() $(p^i_j:X_i\to D_{i,j} \mid j \in J)$
is a limit cone for the J-diagram
$(p^i_j:X_i\to D_{i,j} \mid j \in J)$
is a limit cone for the J-diagram
![]() $D(i,-):J\to \mathbb{A}$
, then the family
$D(i,-):J\to \mathbb{A}$
, then the family
![]() $(X_i \mid i \in I)$
extends canonically to an I-diagram
$(X_i \mid i \in I)$
extends canonically to an I-diagram
![]() $X:I\to \mathbb{A}$
, namely, for
$X:I\to \mathbb{A}$
, namely, for
![]() $f:i\to i'$
in I, the map
$f:i\to i'$
in I, the map
![]() $X_f:X_i\to X_{i'}$
is the unique map in
$X_f:X_i\to X_{i'}$
is the unique map in
![]() $\mathbb{A}$
such that for all
$\mathbb{A}$
such that for all
![]() $j \in J$
, the following diagram commutes:
$j \in J$
, the following diagram commutes:

Moreover, if
![]() $(p_i:x\to X_i \mid i \in I)$
is a limit cone for
$(p_i:x\to X_i \mid i \in I)$
is a limit cone for
![]() $X:I\to \mathbb{A}$
, then
$X:I\to \mathbb{A}$
, then
![]() $(p^i_j\circ p_i:x\to D_{i,j} \mid i \in I, j \in J)$
is a limit cone for D. Since one can exchange the role of I and J, there are two alternative ways of computing limits of
$(p^i_j\circ p_i:x\to D_{i,j} \mid i \in I, j \in J)$
is a limit cone for D. Since one can exchange the role of I and J, there are two alternative ways of computing limits of
![]() $I \times J$
-diagrams, which necessarily produce canonically isomorphic results.
$I \times J$
-diagrams, which necessarily produce canonically isomorphic results.
Proposition 4.4. (Colimits of cofinal diagrams). Given an
![]() $\omega$
-diagram
$\omega$
-diagram
![]() $D:\omega\to \mathbb{A}$
in a category
$D:\omega\to \mathbb{A}$
in a category
![]() $\mathbb{A}$
(with the relevant colimits), if
$\mathbb{A}$
(with the relevant colimits), if
![]() $(f_n:D_n\to X \mid n \in \omega)$
is a colimit cone for D and
$(f_n:D_n\to X \mid n \in \omega)$
is a colimit cone for D and
![]() $h:\omega\to \omega$
is a strictly increasing map, then
$h:\omega\to \omega$
is a strictly increasing map, then
![]() $(f_{h(n)}:D_{h(n)}\to X \mid n \in \omega)$
is a colimit cone for the
$(f_{h(n)}:D_{h(n)}\to X \mid n \in \omega)$
is a colimit cone for the
![]() $\omega$
-diagram
$\omega$
-diagram
![]() $D\circ h:\omega\to \mathbb{A}$
.
$D\circ h:\omega\to \mathbb{A}$
.
4.1 Banach space
 $\mathbb{R}$
$\mathbb{R}$
Consider the metric space
![]() $\mathbb{R}$
with metric
$\mathbb{R}$
with metric
![]() $d(x,y) = \lvert\thinspace {x -y} \thinspace\rvert$
and the
$d(x,y) = \lvert\thinspace {x -y} \thinspace\rvert$
and the
![]() $\omega$
-chain
$\omega$
-chain
![]() $(r_n \mid n \in \omega)$
such that
$(r_n \mid n \in \omega)$
such that

Each
![]() $r_n$
is idempotent and short, because:
$r_n$
is idempotent and short, because:

The image of
![]() $r_n$
is the compact sub-space
$r_n$
is the compact sub-space
![]() $\mathbb{R}_n\stackrel{\triangle}{=} [-n,n]$
, and the union
$\mathbb{R}_n\stackrel{\triangle}{=} [-n,n]$
, and the union
![]() $\mathbb{S}_*$
of the
$\mathbb{S}_*$
of the
![]() $\mathbb{R}_n$
is
$\mathbb{R}_n$
is
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
Let
![]() $(f_n,q_n)$
be the splitting of
$(f_n,q_n)$
be the splitting of
![]() $r_n$
through
$r_n$
through
![]() $\mathbb{R}_n$
in
$\mathbb{R}_n$
in
![]() $\mathbf{Met}$
and
$\mathbf{Met}$
and
![]() $p_n=q_n\circ f_{n+1}:\mathbb{R}_{n+1}\to \mathbb{R}_n$
. Let
$p_n=q_n\circ f_{n+1}:\mathbb{R}_{n+1}\to \mathbb{R}_n$
. Let
![]() $(\overline{q}_n \mid n)$
be the limit cone from
$(\overline{q}_n \mid n)$
be the limit cone from
![]() $\overline{\mathbb{S}}$
to the
$\overline{\mathbb{S}}$
to the
![]() $\omega^{op}$
-chain
$\omega^{op}$
-chain
![]() $(p_n \mid n)$
in
$(p_n \mid n)$
in
![]() $\mathbf{Haus}$
. Then, by Theorem 3.10,
$\mathbf{Haus}$
. Then, by Theorem 3.10,
![]() $\overline{\mathbb{S}}$
is compact, and by Theorem 3.11, the map
$\overline{\mathbb{S}}$
is compact, and by Theorem 3.11, the map
![]() $\iota\,:\,\mathbb{R}\to \overline{\mathbb{S}}$
is both epic and monic in
$\iota\,:\,\mathbb{R}\to \overline{\mathbb{S}}$
is both epic and monic in
![]() $\mathbf{Haus}$
.
$\mathbf{Haus}$
.
We show that
![]() $(\overline{q}_n \mid n)$
is isomorphic to the cone
$(\overline{q}_n \mid n)$
is isomorphic to the cone
![]() $(\hat{q}_n \mid n)$
from
$(\hat{q}_n \mid n)$
from
![]() $\overline{\mathbb{R}}=[-\infty,+\infty]$
(the two-point compactification of
$\overline{\mathbb{R}}=[-\infty,+\infty]$
(the two-point compactification of
![]() $\mathbb{R}$
defined in Example 2.2) to
$\mathbb{R}$
defined in Example 2.2) to
![]() $(p_n \mid n)$
, where
$(p_n \mid n)$
, where
![]() $\hat{q}_n$
is the extension of
$\hat{q}_n$
is the extension of
![]() $q_n$
to
$q_n$
to
![]() $\overline{\mathbb{R}}$
mapping
$\overline{\mathbb{R}}$
mapping
![]() $-\infty$
to
$-\infty$
to
![]() $-n$
and
$-n$
and
![]() $+\infty$
to
$+\infty$
to
![]() $+n$
. Let
$+n$
. Let
![]() $\phi:\overline{\mathbb{R}}\to \overline{\mathbb{S}}$
be the unique map such that
$\phi:\overline{\mathbb{R}}\to \overline{\mathbb{S}}$
be the unique map such that
![]() $\forall n.\hat{q}_n=\overline{q}_n\circ\phi$
, namely
$\forall n.\hat{q}_n=\overline{q}_n\circ\phi$
, namely
![]() $\phi(x)\stackrel{\triangle}{=}(\hat{q}_n(x) \mid n)$
. The map
$\phi(x)\stackrel{\triangle}{=}(\hat{q}_n(x) \mid n)$
. The map
![]() $\phi$
is a bijection (in
$\phi$
is a bijection (in
![]() $\mathbf{Set}$
), since the elements
$\mathbf{Set}$
), since the elements
![]() $(s_n \mid n)$
in
$(s_n \mid n)$
in
![]() $\overline{\mathbb{S}}$
satisfy one of the following disjoint properties:
$\overline{\mathbb{S}}$
satisfy one of the following disjoint properties:
-
 $\forall n.s_n=-n$
, i.e.,
$\forall n.s_n=-n$
, i.e.,
 $(s_n \mid n)=\phi(-\infty)$
;
$(s_n \mid n)=\phi(-\infty)$
; -
 $(s_n \mid n)$
is eventually constant. This happens when
$(s_n \mid n)$
is eventually constant. This happens when
 $\lvert\thinspace {s_m} \thinspace\rvert<m$
for some
$\lvert\thinspace {s_m} \thinspace\rvert<m$
for some
 $m \in \omega$
. In this case
$m \in \omega$
. In this case
 $(s_n \mid n)=\phi(s_m)$
;
$(s_n \mid n)=\phi(s_m)$
; -
 $\forall n.s_n=+n$
, i.e.,
$\forall n.s_n=+n$
, i.e.,
 $(s_n \mid n)=\phi(+\infty)$
.
$(s_n \mid n)=\phi(+\infty)$
.
Therefore,
![]() $(\hat{q}_n \mid n)$
is a limit cone from
$(\hat{q}_n \mid n)$
is a limit cone from
![]() $\overline{\mathbb{R}}$
to
$\overline{\mathbb{R}}$
to
![]() $(p_n \mid n)$
in
$(p_n \mid n)$
in
![]() $\mathbf{Set}$
. To prove that
$\mathbf{Set}$
. To prove that
![]() $\phi$
is an iso in
$\phi$
is an iso in
![]() $\mathbf{Top}$
, it suffices to show that the topology on
$\mathbf{Top}$
, it suffices to show that the topology on
![]() $\overline{\mathbb{R}}$
is the coarsest topology making the maps
$\overline{\mathbb{R}}$
is the coarsest topology making the maps
![]() $\hat{q}_n$
continuous (Proposition 4.2). Since a base for the topology on
$\hat{q}_n$
continuous (Proposition 4.2). Since a base for the topology on
![]() $\overline{\mathbb{R}}$
consists of the subsets of the form
$\overline{\mathbb{R}}$
consists of the subsets of the form
![]() $[-\infty,x)$
, (x,y) and
$[-\infty,x)$
, (x,y) and
![]() $(y,+\infty]$
for
$(y,+\infty]$
for
![]() $x,y \in \mathbb{R}$
, it suffices to show that every element in the base is of the form
$x,y \in \mathbb{R}$
, it suffices to show that every element in the base is of the form
![]() ${\hat{q}_n}^{-1}(O)$
for some
${\hat{q}_n}^{-1}(O)$
for some
![]() $n \in \omega$
and open subset
$n \in \omega$
and open subset
![]() $O \in \mathsf{O}(\mathbb{R}_n)$
. This is immediate by taking n such that
$O \in \mathsf{O}(\mathbb{R}_n)$
. This is immediate by taking n such that
![]() $\lvert\thinspace {x} \thinspace\rvert,\lvert\thinspace {y} \thinspace\rvert<n$
, and taking O of the form
$\lvert\thinspace {x} \thinspace\rvert,\lvert\thinspace {y} \thinspace\rvert<n$
, and taking O of the form
![]() $[-n,x)$
, (x,y) and
$[-n,x)$
, (x,y) and
![]() $(y,+n]$
, respectively.
$(y,+n]$
, respectively.
4.2 Banach spaces
 $\ell_{m,\infty}$
for
$\ell_{m,\infty}$
for
 $1<m$
$1<m$
Fix a natural number
![]() $m>1$
, consider the metric space
$m>1$
, consider the metric space
![]() $\mathbb{S}=\ell_{m,\infty}$
with metric
$\mathbb{S}=\ell_{m,\infty}$
with metric
![]() $d_\infty(x,y)=\max_{i \in m}d(x_i,y_i)$
, which coincides with the product
$d_\infty(x,y)=\max_{i \in m}d(x_i,y_i)$
, which coincides with the product
![]() $\mathbb{R}^m$
in
$\mathbb{R}^m$
in
![]() $\mathbf{Met}$
, and the
$\mathbf{Met}$
, and the
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
, where
$(g_n \mid n)$
, where
where
![]() $r_n$
is as defined in (3). Since
$r_n$
is as defined in (3). Since
![]() $g_n$
is defined pointwise, it is idempotent and short by inheritance, since
$g_n$
is defined pointwise, it is idempotent and short by inheritance, since
![]() $d_\infty(g_n(x),g_n(y))= \max_{i \in m} d(r_n(x_i),r_n(y_i))\leq\max_{i \in m} d(x_i,y_i)= d_\infty(x,y)$
. The image of
$d_\infty(g_n(x),g_n(y))= \max_{i \in m} d(r_n(x_i),r_n(y_i))\leq\max_{i \in m} d(x_i,y_i)= d_\infty(x,y)$
. The image of
![]() $g_n$
is the compact sub-space
$g_n$
is the compact sub-space
![]() $\mathbb{S}_n\stackrel{\triangle}{=}\mathbb{R}_n^m$
and, once again, the union
$\mathbb{S}_n\stackrel{\triangle}{=}\mathbb{R}_n^m$
and, once again, the union
![]() $\mathbb{S}_*$
of the
$\mathbb{S}_*$
of the
![]() $\mathbb{S}_n$
is
$\mathbb{S}_n$
is
![]() $\mathbb{S}$
.From Section 4.1 and Proposition 4.3, we have that
$\mathbb{S}$
.From Section 4.1 and Proposition 4.3, we have that
![]() $\overline{\mathbb{S}}$
is isomorphic to
$\overline{\mathbb{S}}$
is isomorphic to
![]() $\overline{\mathbb{R}}^m$
in
$\overline{\mathbb{R}}^m$
in
![]() $\mathbf{KH}$
. In fact,
$\mathbf{KH}$
. In fact,
![]() $\mathbf{KH}$
has all small limits. Thus, we can take
$\mathbf{KH}$
has all small limits. Thus, we can take
![]() $I=m$
and
$I=m$
and
![]() $J=\omega^{op}$
, and consider the
$J=\omega^{op}$
, and consider the
![]() $I \times J$
-diagram
$I \times J$
-diagram
![]() $D:I \times J\to \mathbf{KH}$
such that
$D:I \times J\to \mathbf{KH}$
such that
![]() $D(i,n)=\mathbb{R}_n$
and
$D(i,n)=\mathbb{R}_n$
and
![]() $D(i,n+1\to n)$
is the map
$D(i,n+1\to n)$
is the map
![]() $p_n:\mathbb{R}_{n+1}\to \mathbb{R}_n$
defined in Section 4.1. The limit
$p_n:\mathbb{R}_{n+1}\to \mathbb{R}_n$
defined in Section 4.1. The limit
![]() $\overline{\mathbb{S}}$
is obtained by first computing the limits
$\overline{\mathbb{S}}$
is obtained by first computing the limits
![]() $\mathbb{R}_n^m$
of I-diagrams
$\mathbb{R}_n^m$
of I-diagrams
![]() $D(-,n)$
and then the J-limit, while
$D(-,n)$
and then the J-limit, while
![]() $\overline{\mathbb{R}}^m$
is obtained by first computing the limits
$\overline{\mathbb{R}}^m$
is obtained by first computing the limits
![]() $\overline{\mathbb{R}}$
of the J-diagrams
$\overline{\mathbb{R}}$
of the J-diagrams
![]() $D(i,-)$
and then the I-limit.
$D(i,-)$
and then the I-limit.
4.3 Banach spaces
 $\ell_{m,p}$
for
$\ell_{m,p}$
for
 $1<m$
and
$1<m$
and
 $1\leq p<\infty$
$1\leq p<\infty$
This is a modification of Section 4.2, where we consider the metric space
![]() $\mathbb{S}=\ell_{m,p}$
that has the carrier of
$\mathbb{S}=\ell_{m,p}$
that has the carrier of
![]() $\ell_{m,\infty}=\mathbb{R}^m$
, but with metric
$\ell_{m,\infty}=\mathbb{R}^m$
, but with metric
 \begin{align*} d_p(x,y)\stackrel{\triangle}{=}\left( \sum_{i \in m} d(x_i,y_i)^p \right)^{1/p}\geq d_\infty(x,y).\end{align*}
\begin{align*} d_p(x,y)\stackrel{\triangle}{=}\left( \sum_{i \in m} d(x_i,y_i)^p \right)^{1/p}\geq d_\infty(x,y).\end{align*}
We take the same
![]() $g_n$
used for
$g_n$
used for
![]() $\ell_{m,\infty}$
, as defined in (4). Clearly
$\ell_{m,\infty}$
, as defined in (4). Clearly
![]() $g_n$
is idempotent, since this property does not depend on the metric, and is short also with respect to
$g_n$
is idempotent, since this property does not depend on the metric, and is short also with respect to
![]() $d_p$
(again by inheritance), since
$d_p$
(again by inheritance), since
 \begin{align*} d_p(g_n(x),g_n(y))= \left(\sum_{i \in m} d(r_n(x_i),r_n(y_i))^p \right)^{1/p} \leq \left( \sum_{i \in m} d(x_i,y_i)^p \right)^{1/p} = d_p(x,y).\end{align*}
\begin{align*} d_p(g_n(x),g_n(y))= \left(\sum_{i \in m} d(r_n(x_i),r_n(y_i))^p \right)^{1/p} \leq \left( \sum_{i \in m} d(x_i,y_i)^p \right)^{1/p} = d_p(x,y).\end{align*}
Thus, the metric space
![]() $\mathbb{S}_n$
has the same carrier of
$\mathbb{S}_n$
has the same carrier of
![]() $\mathbb{R}_n^m$
and metric
$\mathbb{R}_n^m$
and metric
![]() $d_p$
. Since
$d_p$
. Since
![]() $d_p$
and
$d_p$
and
![]() $d_\infty$
induce the same topology on
$d_\infty$
induce the same topology on
![]() $\mathbb{R}_n^m$
, the spaces
$\mathbb{R}_n^m$
, the spaces
![]() $\overline{\mathbb{S}}$
for
$\overline{\mathbb{S}}$
for
![]() $\ell_{m,p}$
and for
$\ell_{m,p}$
and for
![]() $\ell_{m,\infty}$
are equal and isomorphic to
$\ell_{m,\infty}$
are equal and isomorphic to
![]() $\overline{\mathbb{R}}^m$
in
$\overline{\mathbb{R}}^m$
in
![]() $\mathbf{KH}$
.
$\mathbf{KH}$
.
4.4 Banach spaces
 $\ell_{\infty}$
and
$\ell_{\infty}$
and
 $c_0$
$c_0$
Consider the metric space
![]() $\mathbb{S}=\ell_{\infty}$
with metric
$\mathbb{S}=\ell_{\infty}$
with metric
![]() $d_\infty(x,y)\stackrel{\triangle}{=}\sup_{i \in \omega}d(x_i,y_i)$
and the
$d_\infty(x,y)\stackrel{\triangle}{=}\sup_{i \in \omega}d(x_i,y_i)$
and the
![]() $\omega$
-chain
$\omega$
-chain
![]() $(g_n \mid n)$
of idempotents on
$(g_n \mid n)$
of idempotents on
![]() $\ell_{\infty}$
defined by
$\ell_{\infty}$
defined by
Since
![]() $g_n$
is defined pointwise, it is idempotent and short by inheritance, e.g.,
$g_n$
is defined pointwise, it is idempotent and short by inheritance, e.g.,
The image of
![]() $g_n$
is the compact sub-space
$g_n$
is the compact sub-space
![]() $\mathbb{S}_n={\ell_{\infty}}_n\stackrel{\triangle}{=} \mathbb{R}_n^n\times \{0\}^\omega$
, which is isomorphic to the finite product
$\mathbb{S}_n={\ell_{\infty}}_n\stackrel{\triangle}{=} \mathbb{R}_n^n\times \{0\}^\omega$
, which is isomorphic to the finite product
![]() $\mathbb{R}_n^n$
in
$\mathbb{R}_n^n$
in
![]() $\mathbf{Met}$
(since
$\mathbf{Met}$
(since
![]() $\{0\}$
is a terminal object in
$\{0\}$
is a terminal object in
![]() $\mathbf{Met}$
), and the union
$\mathbf{Met}$
), and the union
![]() $\mathbb{S}_*$
of the
$\mathbb{S}_*$
of the
![]() $\mathbb{S}_n$
is the sub-space
$\mathbb{S}_n$
is the sub-space
![]() $\ell_{*,\infty}$
of
$\ell_{*,\infty}$
of
![]() $\omega$
-sequences eventually equal to 0, which is not dense in
$\omega$
-sequences eventually equal to 0, which is not dense in
![]() $\ell_{\infty}$
. For instance, consider
$\ell_{\infty}$
. For instance, consider
![]() $1^\omega \in \ell_{\infty}$
, then
$1^\omega \in \ell_{\infty}$
, then
![]() $\ell_{*,\infty} \cap B(1^\omega, 0.5) = \emptyset$
. The closure of
$\ell_{*,\infty} \cap B(1^\omega, 0.5) = \emptyset$
. The closure of
![]() $\ell_{*,\infty}$
in
$\ell_{*,\infty}$
in
![]() $\ell_{\infty}$
is the sub-space
$\ell_{\infty}$
is the sub-space
![]() $c_0$
of
$c_0$
of
![]() $\omega$
-sequences converging to 0. In functional analysis, the elements of
$\omega$
-sequences converging to 0. In functional analysis, the elements of
![]() $c_0$
are sometimes called null sequences, e.g., see Narici and Beckenstein (Reference Narici and Beckenstein2011).
$c_0$
are sometimes called null sequences, e.g., see Narici and Beckenstein (Reference Narici and Beckenstein2011).
From Section 4.1, Proposition 4.3, and the dual of Proposition 4.4, we have that
![]() $\overline{\mathbb{S}}$
for
$\overline{\mathbb{S}}$
for
![]() $\ell_{\infty}$
, which we denote as
$\ell_{\infty}$
, which we denote as
![]() $\overline{\ell}_{\infty}$
, is isomorphic to
$\overline{\ell}_{\infty}$
, is isomorphic to
![]() $\overline{\mathbb{R}}^\omega$
in
$\overline{\mathbb{R}}^\omega$
in
![]() $\mathbf{KH}$
. In fact, take
$\mathbf{KH}$
. In fact, take
![]() $I=\mathbb{N}$
,
$I=\mathbb{N}$
,
![]() $J=\omega^{op}$
, and consider the
$J=\omega^{op}$
, and consider the
![]() $I\times J$
-diagram
$I\times J$
-diagram
![]() $D:I \times J\to \mathbf{KH}$
such that
$D:I \times J\to \mathbf{KH}$
such that
![]() $D(i,n)=\mathbb{R}_n$
if
$D(i,n)=\mathbb{R}_n$
if
![]() $i<n$
, else
$i<n$
, else
![]() $\{0\}$
, and
$\{0\}$
, and
![]() $D(i,n+1\to n)= p_n: \mathbb{R}_{n+1}\to \mathbb{R}_n$
if
$D(i,n+1\to n)= p_n: \mathbb{R}_{n+1}\to \mathbb{R}_n$
if
![]() $i<n$
, else the unique map from
$i<n$
, else the unique map from
![]() $D(i,n+1)$
to
$D(i,n+1)$
to
![]() $\{0\}$
. The limit
$\{0\}$
. The limit
![]() $\overline{\mathbb{S}}$
is obtained by first computing the limits of I-diagrams
$\overline{\mathbb{S}}$
is obtained by first computing the limits of I-diagrams
![]() $D(-,n)$
, which are isomorphic to
$D(-,n)$
, which are isomorphic to
![]() $\mathbb{R}_n^n$
, and then the J-limit, while
$\mathbb{R}_n^n$
, and then the J-limit, while
![]() $\overline{\mathbb{R}}^\omega$
is obtained by first computing the limits
$\overline{\mathbb{R}}^\omega$
is obtained by first computing the limits
![]() $\overline{\mathbb{R}}$
of the J-diagrams
$\overline{\mathbb{R}}$
of the J-diagrams
![]() $D(i,-)$
and then the I-limit.
$D(i,-)$
and then the I-limit.
Note that the map
![]() $\iota:\ell_{\infty}\to \overline{\ell}_{\infty}$
given by Theorem 3.11 is monic and epic in
$\iota:\ell_{\infty}\to \overline{\ell}_{\infty}$
given by Theorem 3.11 is monic and epic in
![]() $\mathbf{Haus}$
. Moreover, let
$\mathbf{Haus}$
. Moreover, let
![]() $\prod_{i \in \omega} O_i$
be a non-empty basic open set in the topology of
$\prod_{i \in \omega} O_i$
be a non-empty basic open set in the topology of
![]() $\overline{\ell}_{\infty}$
. This means that, for some
$\overline{\ell}_{\infty}$
. This means that, for some
![]() $J \subseteq_f \mathbb{N}$
, we have
$J \subseteq_f \mathbb{N}$
, we have
![]() $\forall i \in \mathbb{N} \setminus J: O_i = \overline{\mathbb{R}}$
. For each
$\forall i \in \mathbb{N} \setminus J: O_i = \overline{\mathbb{R}}$
. For each
![]() $j \in J$
, choose a point
$j \in J$
, choose a point
![]() $y_j \in O_j$
. Then, the sequence
$y_j \in O_j$
. Then, the sequence
![]() $x \in \ell_{*,\infty}$
defined by:
$x \in \ell_{*,\infty}$
defined by:
 \begin{align*} \forall i \in \omega: \quad x_i \stackrel{\triangle}{=} \left\{ \begin{array}{ll} y_i, & \text{ if } i \in J,\\ 0, & \text{ if } i \notin J,\\ \end{array} \right. \end{align*}
\begin{align*} \forall i \in \omega: \quad x_i \stackrel{\triangle}{=} \left\{ \begin{array}{ll} y_i, & \text{ if } i \in J,\\ 0, & \text{ if } i \notin J,\\ \end{array} \right. \end{align*}
is in
![]() $\prod_{i \in \omega} O_i$
. Thus, although
$\prod_{i \in \omega} O_i$
. Thus, although
![]() $\ell_{*,\infty}$
is a subset of both
$\ell_{*,\infty}$
is a subset of both
![]() $\overline{\ell}_{\infty}$
and
$\overline{\ell}_{\infty}$
and
![]() $\ell_{\infty}$
, and, not dense in
$\ell_{\infty}$
, and, not dense in
![]() $\ell_{\infty}$
, it is dense in
$\ell_{\infty}$
, it is dense in
![]() $\overline{\ell}_{\infty}$
. As such,
$\overline{\ell}_{\infty}$
. As such,
![]() $\ell_{\infty}$
is not a sub-space of
$\ell_{\infty}$
is not a sub-space of
![]() $\overline{\ell}_{\infty}$
. In particular,
$\overline{\ell}_{\infty}$
. In particular,
![]() $\overline{\ell}_{\infty}$
is not a compactification of
$\overline{\ell}_{\infty}$
is not a compactification of
![]() $\ell_{\infty}$
.
$\ell_{\infty}$
.
Remark 4.5. Since
![]() $\ell_{\infty}$
is not second-countable, no compactification K of
$\ell_{\infty}$
is not second-countable, no compactification K of
![]() $\ell_{\infty}$
can be second-countable either, and the lattice
$\ell_{\infty}$
can be second-countable either, and the lattice
![]() $\mathbb{C}(K)$
cannot be
$\mathbb{C}(K)$
cannot be
![]() $\omega$
-continuous. The case of
$\omega$
-continuous. The case of
![]() $c_0$
or
$c_0$
or
![]() $\ell_{p}$
with
$\ell_{p}$
with
![]() $1 \leq p < \infty$
is more subtle. These spaces are second-countable and normal, and in theory, it is possible to obtain second-countable compactifications using a variant of the Stone-Čech construction. The problem with the Stone-Čech compactification (and its variants) is that concrete descriptions are either non-existent, or unwieldy, even for relatively simple spaces. As such, these compactification methods are not suitable for an effective framework.
$1 \leq p < \infty$
is more subtle. These spaces are second-countable and normal, and in theory, it is possible to obtain second-countable compactifications using a variant of the Stone-Čech construction. The problem with the Stone-Čech compactification (and its variants) is that concrete descriptions are either non-existent, or unwieldy, even for relatively simple spaces. As such, these compactification methods are not suitable for an effective framework.
4.5 Banach spaces
 $\ell_{p}$
for
$\ell_{p}$
for
 $1\leq p<\infty$
$1\leq p<\infty$
Consider the metric spaces
![]() $\mathbb{S}=\ell_{p}$
with metric
$\mathbb{S}=\ell_{p}$
with metric
![]() $d_p(x,y)\stackrel{\triangle}{=}\left(\sum_{i \in \omega}d(x_i,y_i)^p\right)^{1/p}\geq d_\infty(x,y)$
. The carrier
$d_p(x,y)\stackrel{\triangle}{=}\left(\sum_{i \in \omega}d(x_i,y_i)^p\right)^{1/p}\geq d_\infty(x,y)$
. The carrier
![]() $\lvert\thinspace {\ell_{p}} \thinspace\rvert$
of
$\lvert\thinspace {\ell_{p}} \thinspace\rvert$
of
![]() $\ell_{p}$
satisfies the following strict inclusions
$\ell_{p}$
satisfies the following strict inclusions
We can consider the restrictions to
![]() $\ell_{p}$
of the idempotents
$\ell_{p}$
of the idempotents
![]() $g_n$
defined in (5). It is straightforward to prove that
$g_n$
defined in (5). It is straightforward to prove that
![]() $g_n$
is short and idempotent on
$g_n$
is short and idempotent on
![]() $\ell_{p}$
, its image
$\ell_{p}$
, its image
![]() $\mathbb{S}_n={\ell_{p}}_n$
is isomorphic to the metric space with carrier
$\mathbb{S}_n={\ell_{p}}_n$
is isomorphic to the metric space with carrier
![]() $\mathbb{R}_n^n$
and metric
$\mathbb{R}_n^n$
and metric
![]() $d_p$
, and the union
$d_p$
, and the union
![]() $\mathbb{S}_*$
of the
$\mathbb{S}_*$
of the
![]() $\mathbb{S}_n$
is the dense sub-space
$\mathbb{S}_n$
is the dense sub-space
![]() $\ell_{*,p}$
of
$\ell_{*,p}$
of
![]() $\ell_{p}$
.
$\ell_{p}$
.
By analogy with Section 4.4, we have that the map
![]() $\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
is monic and epic in
$\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
is monic and epic in
![]() $\mathbf{Haus}$
, and
$\mathbf{Haus}$
, and
![]() $\overline{\mathbb{S}}$
for
$\overline{\mathbb{S}}$
for
![]() $\ell_{p}$
is isomorphic to
$\ell_{p}$
is isomorphic to
![]() $\overline{\mathbb{R}}^\omega$
in
$\overline{\mathbb{R}}^\omega$
in
![]() $\mathbf{KH}$
. In particular,
$\mathbf{KH}$
. In particular,
![]() $\overline{\mathbb{S}}$
is independent of p. In summary, the relations between
$\overline{\mathbb{S}}$
is independent of p. In summary, the relations between
![]() $\ell_{p}$
and
$\ell_{p}$
and
![]() $\ell_{q}$
, for
$\ell_{q}$
, for
![]() $1\leq p<q\leq\infty$
, are:
$1\leq p<q\leq\infty$
, are:
-
The carrier of
 $\ell_{p}$
is a proper subset of the carrier of
$\ell_{p}$
is a proper subset of the carrier of
 $\ell_{q}$
, and the inclusion of
$\ell_{q}$
, and the inclusion of
 $\ell_{p}$
into
$\ell_{p}$
into
 $\ell_{q}$
is a short map in
$\ell_{q}$
is a short map in
 $\mathbf{Met}$
, since
$\mathbf{Met}$
, since
 $\forall x,y \in \ell_{p}.d_q(x,y)\leq d_p(x,y)$
.
$\forall x,y \in \ell_{p}.d_q(x,y)\leq d_p(x,y)$
. -
The compact metric spaces
 ${\ell_{p}}_n$
and
${\ell_{p}}_n$
and
 ${\ell_{q}}_n$
have the same carrier, but different metrics, and the inclusion of
${\ell_{q}}_n$
have the same carrier, but different metrics, and the inclusion of
 ${\ell_{p}}_n$
into
${\ell_{p}}_n$
into
 ${\ell_{q}}_n$
is a short map in
${\ell_{q}}_n$
is a short map in
 $\mathbf{KMS}$
.
$\mathbf{KMS}$
. -
As topological spaces,
 ${\ell_{p}}_n$
and
${\ell_{p}}_n$
and
 ${\ell_{q}}_n$
are equal. Thus,
${\ell_{q}}_n$
are equal. Thus,
 $\overline{\ell}_{p}=\overline{\ell}_{q}$
.
$\overline{\ell}_{p}=\overline{\ell}_{q}$
.
4.6 Unit ball
 $B_{\infty}$
$B_{\infty}$
Let us now consider the unit ball
![]() $B_{\infty}$
in the metric space
$B_{\infty}$
in the metric space
![]() $\ell_{\infty}$
. As a metric space,
$\ell_{\infty}$
. As a metric space,
![]() $B_{\infty}$
coincides with the infinite product
$B_{\infty}$
coincides with the infinite product
![]() $\mathbb{R}_1^\omega$
in
$\mathbb{R}_1^\omega$
in
![]() $\mathbf{Met}$
, and the idempotents
$\mathbf{Met}$
, and the idempotents
![]() $g_n$
defined is Section 4.4 restrict to idempotents on
$g_n$
defined is Section 4.4 restrict to idempotents on
![]() $B_{\infty}$
. The image of
$B_{\infty}$
. The image of
![]() $g_n$
(restricted to
$g_n$
(restricted to
![]() $B_{\infty}$
) is the compact sub-space
$B_{\infty}$
) is the compact sub-space
![]() $\mathbb{S}_n={B_{\infty}}_n\stackrel{\triangle}{=}\mathbb{R}_1^n\times \{0\}^\omega$
, which is isomorphic to the finite product
$\mathbb{S}_n={B_{\infty}}_n\stackrel{\triangle}{=}\mathbb{R}_1^n\times \{0\}^\omega$
, which is isomorphic to the finite product
![]() $\mathbb{R}_1^n$
in
$\mathbb{R}_1^n$
in
![]() $\mathbf{Met}$
, and coincides with the closed unit ball
$\mathbf{Met}$
, and coincides with the closed unit ball
![]() $B_{n,\infty}$
in
$B_{n,\infty}$
in
![]() $\ell_{n,\infty}=\mathbb{R}^n$
. The union
$\ell_{n,\infty}=\mathbb{R}^n$
. The union
![]() $\mathbb{S}_*$
of the
$\mathbb{S}_*$
of the
![]() $\mathbb{S}_n$
is the sub-space
$\mathbb{S}_n$
is the sub-space
![]() $B_{*,\infty}$
(as defined in Definition 4.1) and the closure of
$B_{*,\infty}$
(as defined in Definition 4.1) and the closure of
![]() $\mathbb{S}_*$
is the sub-space
$\mathbb{S}_*$
is the sub-space
![]() $B_{\infty}\bigcap c_0$
.
$B_{\infty}\bigcap c_0$
.
Similar to Section 4.4, we can prove that
![]() $\overline{\mathbb{S}}$
for
$\overline{\mathbb{S}}$
for
![]() $B_{\infty}$
, which we denote with
$B_{\infty}$
, which we denote with
![]() $\overline{B}_{\infty}$
, is isomorphic to the product
$\overline{B}_{\infty}$
, is isomorphic to the product
![]() $\mathbb{R}_1^\omega$
in
$\mathbb{R}_1^\omega$
in
![]() $\mathbf{KH}$
. More precisely, take
$\mathbf{KH}$
. More precisely, take
![]() $I=\mathbb{N}$
,
$I=\mathbb{N}$
,
![]() $J=\omega^{op}$
, and consider the
$J=\omega^{op}$
, and consider the
![]() $I \times J$
-diagram
$I \times J$
-diagram
![]() $D:I \times J\to \mathbf{KH}$
such that
$D:I \times J\to \mathbf{KH}$
such that
![]() $D(i,n)=\mathbb{R}_1$
if
$D(i,n)=\mathbb{R}_1$
if
![]() $i<n$
else
$i<n$
else
![]() $\{0\}$
, and
$\{0\}$
, and
![]() $D(i,n+1\to n)$
is the identity on
$D(i,n+1\to n)$
is the identity on
![]() $\mathbb{R}_1$
if
$\mathbb{R}_1$
if
![]() $i<n$
, else the unique map from
$i<n$
, else the unique map from
![]() $D(i,n+1)$
to
$D(i,n+1)$
to
![]() $\{0\}$
.
$\{0\}$
.
As in the case of
![]() $\ell_{\infty}$
, the map
$\ell_{\infty}$
, the map
![]() $\iota:B_{\infty}\to \overline{B}_{\infty}$
given by Theorem 3.11 is monic and epic in
$\iota:B_{\infty}\to \overline{B}_{\infty}$
given by Theorem 3.11 is monic and epic in
![]() $\mathbf{Haus}$
. Moreover, as a set-theoretic map,
$\mathbf{Haus}$
. Moreover, as a set-theoretic map,
![]() $\iota$
is a bijection. In fact, the metric space
$\iota$
is a bijection. In fact, the metric space
![]() $B_{\infty}$
is (equal to) the product
$B_{\infty}$
is (equal to) the product
![]() $\mathbb{R}_1^\omega$
in
$\mathbb{R}_1^\omega$
in
![]() $\mathbf{Met}$
and the topological space
$\mathbf{Met}$
and the topological space
![]() $\overline{B}_{\infty}$
is (isomorphic to) the product
$\overline{B}_{\infty}$
is (isomorphic to) the product
![]() $\mathbb{R}_1^\omega$
in
$\mathbb{R}_1^\omega$
in
![]() $\mathbf{KH}$
. As such, without loss of generality, we assume that the map
$\mathbf{KH}$
. As such, without loss of generality, we assume that the map
![]() $\iota$
is an identity map.
$\iota$
is an identity map.
4.7 Unit ball
 $B_{p}$
for
$B_{p}$
for
 $1 \leq p < \infty$
$1 \leq p < \infty$
Let us now consider the unit ball
![]() $B_{p}$
in the metric space
$B_{p}$
in the metric space
![]() $\ell_{p}$
. One can proceed in analogy with Section 4.6. In particular,
$\ell_{p}$
. One can proceed in analogy with Section 4.6. In particular,
![]() ${B_{p}}_n\stackrel{\triangle}{=}B_{n,p}\times \{0\}^\omega$
is isomorphic to the closed unit ball
${B_{p}}_n\stackrel{\triangle}{=}B_{n,p}\times \{0\}^\omega$
is isomorphic to the closed unit ball
![]() $B_{n,p}$
in
$B_{n,p}$
in
![]() $\ell_{n,p}$
, the map
$\ell_{n,p}$
, the map
![]() $\iota:B_{p}\to\overline{B}_{p}$
given by Theorem 3.11 is monic and epic in
$\iota:B_{p}\to\overline{B}_{p}$
given by Theorem 3.11 is monic and epic in
![]() $\mathbf{Haus}$
.
$\mathbf{Haus}$
.
Moreover, as a set-theoretic map,
![]() $\iota$
is a bijection. The map
$\iota$
is a bijection. The map
![]() $\iota$
is clearly injective. So, it suffices to prove that it is surjective. Let us consider an element
$\iota$
is clearly injective. So, it suffices to prove that it is surjective. Let us consider an element
![]() $(x_n \mid n)$
in
$(x_n \mid n)$
in
![]() $\overline{B}_{p}$
. Each
$\overline{B}_{p}$
. Each
![]() $x_n:{B_{p}}_n$
may differ from
$x_n:{B_{p}}_n$
may differ from
![]() $x_{n+1}$
only in the nth component, namely
$x_{n+1}$
only in the nth component, namely
![]() $x_{n,n}=0$
, while
$x_{n,n}=0$
, while
![]() $x_{n+1,n} \in \mathbb{R}_1$
. Consider
$x_{n+1,n} \in \mathbb{R}_1$
. Consider
![]() $y \in \mathbb{R}_1^\omega$
defined by
$y \in \mathbb{R}_1^\omega$
defined by
![]() $y_n\stackrel{\triangle}{=} x_{n+1,n}$
for
$y_n\stackrel{\triangle}{=} x_{n+1,n}$
for
![]() $n \in \omega$
. We have
$n \in \omega$
. We have
![]() ${{{\lVert\thinspace {y}\thinspace\rVert}}}_p=\lim_{n \to \infty}{{{\lVert\thinspace {x_n}\thinspace\rVert}}}_p\leq 1$
, which entails that
${{{\lVert\thinspace {y}\thinspace\rVert}}}_p=\lim_{n \to \infty}{{{\lVert\thinspace {x_n}\thinspace\rVert}}}_p\leq 1$
, which entails that
![]() $y \in B_{p}$
. Furthermore,
$y \in B_{p}$
. Furthermore,
 \begin{align*} \forall i,n \in \omega. \quad x_{n,i}= \left\{ \begin{array}{ll} y_i, & \text{ if } i < n,\\ 0, & \text{otherwise}. \end{array} \right.\end{align*}
\begin{align*} \forall i,n \in \omega. \quad x_{n,i}= \left\{ \begin{array}{ll} y_i, & \text{ if } i < n,\\ 0, & \text{otherwise}. \end{array} \right.\end{align*}
Hence,
![]() $\iota(y) = (x_n \mid n)$
, and
$\iota(y) = (x_n \mid n)$
, and
![]() $\iota$
is surjective. The relations among the
$\iota$
is surjective. The relations among the
![]() $\ell_{p}$
spaces established in Section 4.5 imply the following relations among unit balls, for
$\ell_{p}$
spaces established in Section 4.5 imply the following relations among unit balls, for
![]() $1\leq p<q\leq\infty$
:
$1\leq p<q\leq\infty$
:
-
The carrier of
 $B_{p}$
is a proper subset of the carrier of
$B_{p}$
is a proper subset of the carrier of
 $B_{q}$
, and the inclusion of
$B_{q}$
, and the inclusion of
 $B_{p}$
into
$B_{p}$
into
 $B_{q}$
is a short map in
$B_{q}$
is a short map in
 $\mathbf{Met}$
.
$\mathbf{Met}$
. -
The carrier of
 ${B_{p}}_n$
is a proper subset of the carrier of
${B_{p}}_n$
is a proper subset of the carrier of
 ${B_{q}}_n$
, and the inclusion of
${B_{q}}_n$
, and the inclusion of
 ${B_{p}}_n$
into
${B_{p}}_n$
into
 ${B_{q}}_n$
is a short map in
${B_{q}}_n$
is a short map in
 $\mathbf{KMS}$
.
$\mathbf{KMS}$
. -
As a topological space,
 ${B_{p}}_n$
is a closed sub-space of
${B_{p}}_n$
is a closed sub-space of
 ${B_{q}}_n$
in
${B_{q}}_n$
in
 $\mathbf{KH}$
, since the metrics
$\mathbf{KH}$
, since the metrics
 $d_p$
and
$d_p$
and
 $d_q$
induce the same topology on
$d_q$
induce the same topology on
 $\mathbb{R}^n$
. Thus,
$\mathbb{R}^n$
. Thus,
 $\overline{B}_{p}$
is a closed sub-space of
$\overline{B}_{p}$
is a closed sub-space of
 $\overline{B}_{q}$
in
$\overline{B}_{q}$
in
 $\mathbf{KH}$
.
$\mathbf{KH}$
.
The last point implies that the carrier of
![]() $\overline{B}_{p}$
depends on p, but its topology is that on
$\overline{B}_{p}$
depends on p, but its topology is that on
![]() $\overline{B}_{\infty}$
.
$\overline{B}_{\infty}$
.
5 Precision
Figure 5 gives a summary of the examples in Section 4. We observe the following:
-
(1) In the finite-dimensional cases,
 $\mathbb{S}$
is a dense sub-space of
$\mathbb{S}$
is a dense sub-space of
 $\overline{\mathbb{S}}$
in
$\overline{\mathbb{S}}$
in
 $\mathbf{Haus}$
, and
$\mathbf{Haus}$
, and
 $\overline{\mathbb{S}}$
is a compactification of
$\overline{\mathbb{S}}$
is a compactification of
 $\mathbb{S}$
. Therefore, every closed subset C of
$\mathbb{S}$
. Therefore, every closed subset C of
 $\mathbb{S}$
is the intersection
$\mathbb{S}$
is the intersection
 $C' \bigcap \mathbb{S}$
for some closed subset C’ of
$C' \bigcap \mathbb{S}$
for some closed subset C’ of
 $\overline{\mathbb{S}}$
. Since the metrics
$\overline{\mathbb{S}}$
. Since the metrics
 $d_p$
and
$d_p$
and
 $d_\infty$
induce the same topology on
$d_\infty$
induce the same topology on
 $\mathbb{R}^m$
—the carrier of both
$\mathbb{R}^m$
—the carrier of both
 $\ell_{m,p}$
and
$\ell_{m,p}$
and
 $\ell_{m,\infty}$
—we have
$\ell_{m,\infty}$
—we have
 $\mathbb{C}(\ell_{m,p})=\mathbb{C}(\ell_{m,\infty})$
for each
$\mathbb{C}(\ell_{m,p})=\mathbb{C}(\ell_{m,\infty})$
for each
 $p \in [1, \infty]$
. Furthermore,
$p \in [1, \infty]$
. Furthermore,
 $\overline{\mathbb{S}}$
does not depend on p. Hence, it suffices to consider the cases
$\overline{\mathbb{S}}$
does not depend on p. Hence, it suffices to consider the cases
 $\mathbb{S}=\ell_{m,\infty}$
. The map
$\mathbb{S}=\ell_{m,\infty}$
. The map
 $\iota: \ell_{m,\infty} \to \overline{\ell}_{m,\infty}$
is a sub-space inclusion and
$\iota: \ell_{m,\infty} \to \overline{\ell}_{m,\infty}$
is a sub-space inclusion and
 $\iota^*\circ \iota_* = \text{id}_{\mathbb{C}(\ell_{m,\infty})}$
.
$\iota^*\circ \iota_* = \text{id}_{\mathbb{C}(\ell_{m,\infty})}$
. -
(2) In the infinite-dimensional cases—as we will demonstrate—
 $\mathbb{S}$
is not a sub-space of
$\mathbb{S}$
is not a sub-space of
 $\overline{\mathbb{S}}$
. More precisely,
$\overline{\mathbb{S}}$
. More precisely,
 $\iota: \mathbb{S} \to \overline{\mathbb{S}}$
is monic and epic; thus, the image of
$\iota: \mathbb{S} \to \overline{\mathbb{S}}$
is monic and epic; thus, the image of
 $\iota$
is dense in
$\iota$
is dense in
 $\overline{\mathbb{S}}$
. However,
$\overline{\mathbb{S}}$
. However,
 $\iota$
is not a sub-space inclusion; thus, there are closed subsets C of
$\iota$
is not a sub-space inclusion; thus, there are closed subsets C of
 $\mathbb{S}$
which cannot be written as
$\mathbb{S}$
which cannot be written as
 $C' \bigcap \mathbb{S}$
for some closed subset C’ of
$C' \bigcap \mathbb{S}$
for some closed subset C’ of
 $\overline{\mathbb{S}}$
, and
$\overline{\mathbb{S}}$
, and
 $\iota^*\circ \iota_*$
is not the identity on
$\iota^*\circ \iota_*$
is not the identity on
 $\mathbb{C}(\mathbb{S})$
.
$\mathbb{C}(\mathbb{S})$
.
In what follows, we focus mainly on the case of the unit ball
![]() $B_{p}$
. As discussed in Sections 4.6 and 4.7, without loss of generality, we assume that the bijective map
$B_{p}$
. As discussed in Sections 4.6 and 4.7, without loss of generality, we assume that the bijective map
![]() $\iota:B_{p}\to \overline{B}_{p}$
is an identity. As a result, by going from
$\iota:B_{p}\to \overline{B}_{p}$
is an identity. As a result, by going from
![]() $B_{p}$
to
$B_{p}$
to
![]() $\overline{B}_{p}$
, the carrier does not change, and we have to compare only the topologies, or equivalently
$\overline{B}_{p}$
, the carrier does not change, and we have to compare only the topologies, or equivalently
![]() $\mathbb{C}(\overline{B}_{p})\subset\mathbb{C}(B_{p})$
. Since the left adjoint
$\mathbb{C}(\overline{B}_{p})\subset\mathbb{C}(B_{p})$
. Since the left adjoint
![]() $\iota^*$
is the inclusion map of
$\iota^*$
is the inclusion map of
![]() $\mathbb{C}(\overline{B}_{p})$
into
$\mathbb{C}(\overline{B}_{p})$
into
![]() $\mathbb{C}(B_{p})$
, we have
$\mathbb{C}(B_{p})$
, we have
![]() $\iota^*(\iota_*(C))=\iota_*(C)$
. Thus, the loss of precision is measured by how bigger is
$\iota^*(\iota_*(C))=\iota_*(C)$
. Thus, the loss of precision is measured by how bigger is
![]() $\iota_*(C)$
in comparison to the closed subset C in
$\iota_*(C)$
in comparison to the closed subset C in
![]() $\mathbb{C}(B_{p})$
.
$\mathbb{C}(B_{p})$
.
Remark 5.1. In applications, it is reasonable to restrict to closed bounded subsets of Banach spaces, i.e., closed subsets included in a ball of finite radius. The claims in this section are true for closed balls in
![]() $\ell_{p}$
with center x and radius
$\ell_{p}$
with center x and radius
![]() $r>0$
, but we state them for the paradigmatic case
$r>0$
, but we state them for the paradigmatic case
![]() $x=0$
and
$x=0$
and
![]() $r=1$
, to avoid extra parameters in notation. Note that, compact subsets of a Banach space are always closed and bounded, and in the finite-dimensional case the converse also holds.
$r=1$
, to avoid extra parameters in notation. Note that, compact subsets of a Banach space are always closed and bounded, and in the finite-dimensional case the converse also holds.
To start, we present a positive result where there is no loss of precision.
Proposition 5.2 (Compact sets). If
![]() is a mono in
is a mono in
![]() $\mathbf{Haus}$
, then compact subsets of
$\mathbf{Haus}$
, then compact subsets of
![]() $\mathbb{S}_1$
are compact in
$\mathbb{S}_1$
are compact in
![]() $\mathbb{S}_2$
.
$\mathbb{S}_2$
.
Proof. Write
![]() $\iota$
for the mono
$\iota$
for the mono
![]() which we can assume to be an inclusion between the carriers. Since
which we can assume to be an inclusion between the carriers. Since
![]() $\iota$
is continuous, the claim now follows from the general fact that the image of a compact set under a continuous function is always compact.
$\iota$
is continuous, the claim now follows from the general fact that the image of a compact set under a continuous function is always compact.
Corollary 5.3.
Assume that
![]() $\mathbb{S}:\mathbf{Haus}$
, and
$\mathbb{S}:\mathbf{Haus}$
, and
![]() $\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
(in
$\iota\,:\,\mathbb{S}\to \overline{\mathbb{S}}$
(in
![]() $\mathbf{Haus}$
) is as in Theorem 3.11. If
$\mathbf{Haus}$
) is as in Theorem 3.11. If
![]() $C \in \mathbb{C}(\mathbb{S})$
is compact, then
$C \in \mathbb{C}(\mathbb{S})$
is compact, then
![]() $C \in \mathbb{C}(\overline{\mathbb{S}})$
, and therefore
$C \in \mathbb{C}(\overline{\mathbb{S}})$
, and therefore
![]() $\iota_*(C)=C$
.
$\iota_*(C)=C$
.
Proof. As
![]() is mono, by Proposition 5.2, every compact
is mono, by Proposition 5.2, every compact
![]() $C \in \mathbb{C}(\mathbb{S})$
is also compact in
$C \in \mathbb{C}(\mathbb{S})$
is also compact in
![]() $\overline{\mathbb{S}}$
. The result now follows from the fact that in Hausdorff spaces, compact subsets are closed.
$\overline{\mathbb{S}}$
. The result now follows from the fact that in Hausdorff spaces, compact subsets are closed.
Compact subsets of infinite-dimensional Banach spaces are not so relevant in applications (e.g., they always have empty interior). For
![]() $1 < p < \infty$
, however, we have a characterization of the closed bounded subsets of
$1 < p < \infty$
, however, we have a characterization of the closed bounded subsets of
![]() $\ell_{p}$
for which there is no loss of precision, i.e.,
$\ell_{p}$
for which there is no loss of precision, i.e.,
![]() $C=\iota^*(\iota_*(C))$
.
$C=\iota^*(\iota_*(C))$
.
Theorem 5.4. (No loss of Precision). For any
![]() $1 < p < \infty$
and
$1 < p < \infty$
and
![]() $C \in \mathbb{C}(\ell_{p})$
, the following are equivalent:
$C \in \mathbb{C}(\ell_{p})$
, the following are equivalent:
-
(1) C is bounded and
 $C=\iota^*(\iota_*(C))$
, i.e., there is no loss of precision over C.
$C=\iota^*(\iota_*(C))$
, i.e., there is no loss of precision over C. -
(2) C is a non-empty intersection of finite unions of closed balls in
 $\ell_{p}$
.
$\ell_{p}$
. -
(3) C is a non-empty intersection of finite unions of bounded-closed-convex subsets of
 $\ell_{p}$
.
$\ell_{p}$
.
Proof. See the proof 31.
To prove Theorem 5.4, we relate the topology on
![]() $\overline{B}_{p}$
(indeed on any closed ball in
$\overline{B}_{p}$
(indeed on any closed ball in
![]() $\ell_{p}$
) to the weak-* topology, one of the fundamental topologies studied in functional analysis.
$\ell_{p}$
) to the weak-* topology, one of the fundamental topologies studied in functional analysis.
5.1 Weak-* topology on
 $\lvert\thinspace {B_{p}} \thinspace\rvert$
for
$\lvert\thinspace {B_{p}} \thinspace\rvert$
for
 $1 \leq p \leq \infty$
$1 \leq p \leq \infty$
Let us first present a quick reminder of weak and weak-* topologies for the case of normed vector spaces over the field of real numbers. The reader may refer to any standard book on functional analysis, e.g., Conway (Reference Conway1990); Rudin (Reference Rudin1991), for the more general treatment of these topologies.
Definition 5.5 (dual). Given
![]() $X:\mathbf{NVS}$
with norm
$X:\mathbf{NVS}$
with norm
![]() ${{{\lVert\thinspace {.}\thinspace\rVert}}}_X$
, its continuous dual X’ is the Banach space of linear continuous functions from X to
${{{\lVert\thinspace {.}\thinspace\rVert}}}_X$
, its continuous dual X’ is the Banach space of linear continuous functions from X to
![]() $\mathbb{R}$
with norm
$\mathbb{R}$
with norm
![]() ${{{\lVert\thinspace {f}\thinspace\rVert}}}_{X'} \stackrel{\triangle}{=} \sup {{\{{\lvert\thinspace {f(x)} \thinspace\rvert} \mid{x \in X \wedge {{{\lVert\thinspace {x}\thinspace\rVert}}}_{X} \leq 1}\}}}$
.
${{{\lVert\thinspace {f}\thinspace\rVert}}}_{X'} \stackrel{\triangle}{=} \sup {{\{{\lvert\thinspace {f(x)} \thinspace\rvert} \mid{x \in X \wedge {{{\lVert\thinspace {x}\thinspace\rVert}}}_{X} \leq 1}\}}}$
.
Proposition 5.6.
If
![]() $Y:\mathbf{Ban}$
is the Cauchy completion of
$Y:\mathbf{Ban}$
is the Cauchy completion of
![]() $X:\mathbf{NVS}$
, then Y’ and X’ are isomorphic.
$X:\mathbf{NVS}$
, then Y’ and X’ are isomorphic.
Proof. See, e.g., Narici and Beckenstein (Reference Narici and Beckenstein2011, Page 270).
Definition 5.7 (reflexive, weak, weak-*). For
![]() $X:\mathbf{NVS}$
, the map
$X:\mathbf{NVS}$
, the map
![]() $\eta_X:X\to X''$
(a linear isometry) is defined as
$\eta_X:X\to X''$
(a linear isometry) is defined as
![]() $\eta_X(x)(f)\stackrel{\triangle}{=} f(x)$
for
$\eta_X(x)(f)\stackrel{\triangle}{=} f(x)$
for
![]() $x \in X$
and
$x \in X$
and
![]() $f \in X'$
. When the map
$f \in X'$
. When the map
![]() $\eta_X$
is an iso, X is called reflexive
.
$\eta_X$
is an iso, X is called reflexive
.
-
(1) The weak topology
 $W_X$
on X is the coarsest topology making each
$W_X$
on X is the coarsest topology making each
 $f \in X'$
continuous.
$f \in X'$
continuous. -
(2) The weak-* topology
 $W_X^*$
on X’ is the coarsest topology on X’ making
$W_X^*$
on X’ is the coarsest topology on X’ making
 $\eta_X(x)$
continuous for each
$\eta_X(x)$
continuous for each
 $x \in X$
.
$x \in X$
.
Proposition 5.8.
Let the conjugate p’ of p be the unique
![]() $q \in [1,\infty]$
such that
$q \in [1,\infty]$
such that
![]() $1/p+1/q=1$
.
$1/p+1/q=1$
.
-
(1) For every
 $p \in [1,\infty)$
, the Cauchy completion of
$p \in [1,\infty)$
, the Cauchy completion of
 $\ell_{*,p}$
is the Banach space
$\ell_{*,p}$
is the Banach space
 $\ell_{p}$
.
$\ell_{p}$
. -
(2) The Cauchy completion of
 $\ell_{*,\infty}$
is the Banach sub-space
$\ell_{*,\infty}$
is the Banach sub-space
 $c_0$
of
$c_0$
of
 $\ell_{\infty}$
.
$\ell_{\infty}$
. -
(3) For every
 $p \in [1,\infty]$
, the map
$p \in [1,\infty]$
, the map
 $\xi:\ell_{p'}\to (\ell_{*,p})'$
, given by
$\xi:\ell_{p'}\to (\ell_{*,p})'$
, given by
 $\xi(x')(x)\stackrel{\triangle}{=}\sum_{i \in \omega} x'_i*x_i$
, is an iso.
$\xi(x')(x)\stackrel{\triangle}{=}\sum_{i \in \omega} x'_i*x_i$
, is an iso.
Proof. Proofs of (1) and (2) are straightforward. To prove (3), by Proposition 5.6, and by (1) and (2), we may regard
![]() $\xi$
as a function from
$\xi$
as a function from
![]() $\ell_{p'}$
to
$\ell_{p'}$
to
![]() $(\ell_{p})'$
, when
$(\ell_{p})'$
, when
![]() $p \in [1,\infty)$
, or to
$p \in [1,\infty)$
, or to
![]() $(c_0)'$
, when
$(c_0)'$
, when
![]() $p = \infty$
. The proof that
$p = \infty$
. The proof that
![]() $\xi$
is an iso may now be found in:
$\xi$
is an iso may now be found in:
-
Conway (Reference Conway1990, Appendix B), for
 $p \in [1,\infty)$
.
$p \in [1,\infty)$
. -
Albiac and Kalton (Reference Albiac and Kalton2006, Page 50), for
 $p=\infty$
.
$p=\infty$
.
The duals and double duals of relevance in this section are summarized in Table 1.
Table 1. Some duals and double duals (up to iso)

Definition 5.9. (Topologies
![]() $\tau_p, \tau_p^*, {\overline{\tau}}_p$
). We define the following topologies on the carrier of
$\tau_p, \tau_p^*, {\overline{\tau}}_p$
). We define the following topologies on the carrier of
![]() $\ell_{p}$
:
$\ell_{p}$
:
-
(1)
 $\tau_p$
is the original (or, norm) topology on
$\tau_p$
is the original (or, norm) topology on
 $\ell_{p}$
, i.e., the topology induced by the norm
$\ell_{p}$
, i.e., the topology induced by the norm
 ${{{\lVert\thinspace {.}\thinspace\rVert}}}_p$
.
${{{\lVert\thinspace {.}\thinspace\rVert}}}_p$
. -
(2)
 denotes the weak-* topology on
denotes the weak-* topology on
 $\ell_{p}$
as the continuous dual of
$\ell_{p}$
as the continuous dual of
 $\ell_{*,p'}$
.
$\ell_{*,p'}$
. -
(3)
 is the topology on
is the topology on
 $\ell_{p}$
as a subset of the compact Hausdorff space
$\ell_{p}$
as a subset of the compact Hausdorff space
 $\overline{\mathbb{R}}^\omega$
.
$\overline{\mathbb{R}}^\omega$
.
We use the same notation for the topologies when restricted to a subset of
![]() $\ell_{p}$
, such as
$\ell_{p}$
, such as
![]() $B_{p}$
.
$B_{p}$
.
According to Figure 5, by using the notation of Definition 5.9, we have that
![]() $\overline{\mathbb{S}} =(\lvert\thinspace {B_{p}} \thinspace\rvert, {\bar{\tau}}_p)$
when
$\overline{\mathbb{S}} =(\lvert\thinspace {B_{p}} \thinspace\rvert, {\bar{\tau}}_p)$
when
![]() $\mathbb{S} = (\lvert\thinspace {B_{p}} \thinspace\rvert,\tau_p)$
. Therefore, we obtain:
$\mathbb{S} = (\lvert\thinspace {B_{p}} \thinspace\rvert,\tau_p)$
. Therefore, we obtain:
Proposition 5.10.
For every
![]() $C \in \mathbb{C}(\ell_{p})$
, the set
$C \in \mathbb{C}(\ell_{p})$
, the set
![]() $\iota^*(\iota_*(C))$
is the
$\iota^*(\iota_*(C))$
is the
![]() ${\overline{\tau}}_p$
closure of C.
${\overline{\tau}}_p$
closure of C.
In Theorem 5.12, we show that the topological spaces
![]() $(\lvert\thinspace {B_{p}} \thinspace\rvert, {\bar{\tau}}_p)$
and
$(\lvert\thinspace {B_{p}} \thinspace\rvert, {\bar{\tau}}_p)$
and
![]() $(\lvert\thinspace {B_{p}} \thinspace\rvert, \tau_p^*)$
coincide for any
$(\lvert\thinspace {B_{p}} \thinspace\rvert, \tau_p^*)$
coincide for any
![]() $1 \leq p \leq \infty$
. First, we recall the lemma on the “rigidity” of compact Hausdorff topologies in Rudin (Reference Rudin1991, Section 3.8).
$1 \leq p \leq \infty$
. First, we recall the lemma on the “rigidity” of compact Hausdorff topologies in Rudin (Reference Rudin1991, Section 3.8).
Lemma 5.11.
If
![]() $\tau_1 \subseteq \tau_2$
are topologies on a set X, with
$\tau_1 \subseteq \tau_2$
are topologies on a set X, with
![]() $\tau_1$
Hausdorff and
$\tau_1$
Hausdorff and
![]() $\tau_2$
compact, then
$\tau_2$
compact, then
![]() $\tau_1 = \tau_2$
.
$\tau_1 = \tau_2$
.
Proof. Let
![]() $F \subseteq X$
be
$F \subseteq X$
be
![]() $\tau_2$
-closed. Since X is
$\tau_2$
-closed. Since X is
![]() $\tau_2$
-compact, so is F. Since
$\tau_2$
-compact, so is F. Since
![]() $\tau_1 \subseteq \tau_2$
, it follows that F is
$\tau_1 \subseteq \tau_2$
, it follows that F is
![]() $\tau_1$
-compact. Since
$\tau_1$
-compact. Since
![]() $\tau_1$
is a Hausdorff topology, it follows that F is
$\tau_1$
is a Hausdorff topology, it follows that F is
![]() $\tau_1$
-closed.
$\tau_1$
-closed.
Theorem 5.12.
For each
![]() $1 \leq p \leq \infty$
,
$1 \leq p \leq \infty$
,
![]() $\overline{B}_{p}$
is (isomorphic to) the topological space
$\overline{B}_{p}$
is (isomorphic to) the topological space
![]() $(\lvert\thinspace {B_{p}} \thinspace\rvert, \tau_p^*)$
.
$(\lvert\thinspace {B_{p}} \thinspace\rvert, \tau_p^*)$
.
Proof. The topology
![]() ${\overline{\tau}}_p$
is Hausdorff. On the other hand, by the Banach-Alaoglu theorem (see, e.g., Rudin (Reference Rudin1991, Section 3.8)) the closed unit ball
${\overline{\tau}}_p$
is Hausdorff. On the other hand, by the Banach-Alaoglu theorem (see, e.g., Rudin (Reference Rudin1991, Section 3.8)) the closed unit ball
![]() $\lvert\thinspace {B_{p}} \thinspace\rvert$
is weak-* compact, i.e.,
$\lvert\thinspace {B_{p}} \thinspace\rvert$
is weak-* compact, i.e.,
![]() $\tau_p^*$
-compact. Therefore, by Lemma 5.11, it suffices to prove that
$\tau_p^*$
-compact. Therefore, by Lemma 5.11, it suffices to prove that
![]() ${\overline{\tau}}_p \subseteq \tau_p^*$
.
${\overline{\tau}}_p \subseteq \tau_p^*$
.
For
![]() $i \in \omega$
, consider the retractions
$i \in \omega$
, consider the retractions
![]() $\pi_i : \ell_{p} \to \mathbb{R}$
defined by
$\pi_i : \ell_{p} \to \mathbb{R}$
defined by
The set
![]() ${\mathcal{Y}} = {{\{{ \lvert\thinspace {B_{p}} \thinspace\rvert \bigcap \pi_i^{-1}(O)} \mid{i \in \omega, O \subseteq \mathbb{R} \text{ Euclidean open}}\}}}$
is a sub-base for
${\mathcal{Y}} = {{\{{ \lvert\thinspace {B_{p}} \thinspace\rvert \bigcap \pi_i^{-1}(O)} \mid{i \in \omega, O \subseteq \mathbb{R} \text{ Euclidean open}}\}}}$
is a sub-base for
![]() ${\overline{\tau}}_p$
. For each
${\overline{\tau}}_p$
. For each
![]() $i \in \omega$
, consider the sequence
$i \in \omega$
, consider the sequence
![]() $e_i$
defined by
$e_i$
defined by
 \begin{equation} \forall n \in \omega. \quad e_i(n) \stackrel{\triangle}{=} \left\{ \begin{array}{ll} 0,& \text{ if } i \neq n,\\ 1, & \text{ if } i = n.\\ \end{array} \right.\end{equation}
\begin{equation} \forall n \in \omega. \quad e_i(n) \stackrel{\triangle}{=} \left\{ \begin{array}{ll} 0,& \text{ if } i \neq n,\\ 1, & \text{ if } i = n.\\ \end{array} \right.\end{equation}
For all
![]() $i \in \omega$
, the sequence
$i \in \omega$
, the sequence
![]() $e_i$
is in all the relevant pre-duals as specified in Definition 5.9 above. Furthermore
$e_i$
is in all the relevant pre-duals as specified in Definition 5.9 above. Furthermore
Thus, each
![]() $\pi_i$
is weak-* continuous and
$\pi_i$
is weak-* continuous and
![]() ${\mathcal{Y}} \subseteq \tau_P^*$
, which entails that
${\mathcal{Y}} \subseteq \tau_P^*$
, which entails that
![]() ${\overline{\tau}}_p \subseteq \tau_P^*$
.
${\overline{\tau}}_p \subseteq \tau_P^*$
.
Remark 5.13. As pointed out in Remark 5.1, although we present results for closed unit balls, they hold for arbitrary closed balls. In particular, Theorem 5.12 holds for closed balls in
![]() $\ell_{p}$
, because they are all
$\ell_{p}$
, because they are all
![]() $\tau_p^*$
-compact.
$\tau_p^*$
-compact.
Corollary 5.14
For each
![]() $1 \leq p \leq \infty$
and
$1 \leq p \leq \infty$
and
![]() $C \in \mathbb{C}(B_{p})$
,
$C \in \mathbb{C}(B_{p})$
,
![]() $\iota_*(C) = C$
iff C is a
$\iota_*(C) = C$
iff C is a
![]() $\tau_p^*$
-closed subset.
$\tau_p^*$
-closed subset.
Corollary 5.15
For each
![]() $1 < p < \infty$
and
$1 < p < \infty$
and
![]() $C \in \mathbb{C}(B_{p})$
,
$C \in \mathbb{C}(B_{p})$
,
![]() $\iota_*(C) = C$
iff C is a weakly closed subset.
$\iota_*(C) = C$
iff C is a weakly closed subset.
Proof. Since the space
![]() $\ell_{p}$
for
$\ell_{p}$
for
![]() $1 < p < \infty$
is reflexive, i.e., the weak and weak-* topologies on
$1 < p < \infty$
is reflexive, i.e., the weak and weak-* topologies on
![]() $\ell_{p}$
coincide. The result follows from Corollary 5.14.
$\ell_{p}$
coincide. The result follows from Corollary 5.14.
We have established all the preliminaries for presenting the proof of Theorem 5.4:
Proof. (Theorem 5.4)
(1)⇒(2) As C is assumed to be bounded, then it must be a subset of a closed ball B of finite radius. If
![]() $\iota^*(\iota_*(C)) = C$
, then, by Corollary 5.15, C must be weakly closed. Thus, C is a weakly closed subset of (the weakly compact set) B. As a result, it is weakly compact.
$\iota^*(\iota_*(C)) = C$
, then, by Corollary 5.15, C must be weakly closed. Thus, C is a weakly closed subset of (the weakly compact set) B. As a result, it is weakly compact.
According to Corson and Lindenstrauss (Reference Corson and Lindenstrauss1966, Theorem 3), a subset of a separable reflexive space is weakly compact if and only if it is the non-empty intersection of finite unions of closed balls. Each space
![]() $\ell_p$
for
$\ell_p$
for
![]() $1 < p < \infty$
is separable and reflexive. Hence, the result follows.
$1 < p < \infty$
is separable and reflexive. Hence, the result follows.
(2)⇒(3) This is straightforward as every closed ball is a bounded-closed-convex subset.
(3)⇒(1) Assume that C is a non-empty intersection of finite unions of bounded-closed-convex subsets of
![]() $\ell_{p}$
. To be precise,
$\ell_{p}$
. To be precise,
![]() $C = \bigcap_{i \in I} \bigcup_{j \in k_i} C_{i,j}$
with
$C = \bigcap_{i \in I} \bigcup_{j \in k_i} C_{i,j}$
with
![]() $k \in \omega^I$
and
$k \in \omega^I$
and
![]() $C_{i,j}$
bounded-closed-convex subset of
$C_{i,j}$
bounded-closed-convex subset of
![]() $\ell_{p}$
.
$\ell_{p}$
.
As a consequence of Hahn-Banach separation theorem, every closed and convex subset of a Banach space is weakly closed (see, e.g., Rudin (Reference Rudin1991, Theorem 3.12)). This entails that each
![]() $C_{i,j}$
is weakly closed. As the set of closed subsets (under any topology) are closed under finite unions and arbitrary intersections, then C itself is also weakly closed. Clearly, C is also bounded. The result now follows from Corollary 5.15.
$C_{i,j}$
is weakly closed. As the set of closed subsets (under any topology) are closed under finite unions and arbitrary intersections, then C itself is also weakly closed. Clearly, C is also bounded. The result now follows from Corollary 5.15.
Item (3) of Theorem 5.4 provides examples where no loss of precision is incurred.
Example 5.16. (Sequence intervals). For a pair
![]() $s,t \in \ell_{p}$
, the sequence interval [s,t] is given by:
$s,t \in \ell_{p}$
, the sequence interval [s,t] is given by:
In general, sequence intervals are not norm-compact in
![]() $\ell_{p}$
, but they are bounded, norm-closed, and convex. Hence, when
$\ell_{p}$
, but they are bounded, norm-closed, and convex. Hence, when
![]() $1 < p <\infty$
, there is no loss of precision over sequence intervals.
$1 < p <\infty$
, there is no loss of precision over sequence intervals.
5.1.1 Metrizability of the
 ${\overline{\tau}}_p$
-topologies over bounded closed balls
${\overline{\tau}}_p$
-topologies over bounded closed balls
Consider the map
![]() $d_* : \ell_{\infty} \times \ell_{\infty} \to \mathbb{R}$
defined as follows:
$d_* : \ell_{\infty} \times \ell_{\infty} \to \mathbb{R}$
defined as follows:
It is straightforward to prove that
![]() $d_*$
is a metric on the carrier of
$d_*$
is a metric on the carrier of
![]() $\ell_{\infty}$
.
$\ell_{\infty}$
.
Proposition 5.17.
The metric
![]() $d_*$
induces the
$d_*$
induces the
![]() ${\overline{\tau}}_\infty$
-topology on closed balls of finite radius in
${\overline{\tau}}_\infty$
-topology on closed balls of finite radius in
![]() $\ell_{\infty}$
.
$\ell_{\infty}$
.
Proof. According to Rudin (Reference Rudin1991, Section 3.8(c), page 63), if X is a compact topological space and if some uniformly bounded sequence
![]() $(f_n \mid {n \in \omega})$
of continuous real-valued functions separates points on X, then X is metrizable, with the metric
$(f_n \mid {n \in \omega})$
of continuous real-valued functions separates points on X, then X is metrizable, with the metric
![]() $\rho(x,y) = \sum_{n \in \omega} 2^{-n} d(f_n(x), f_n(y))$
.
$\rho(x,y) = \sum_{n \in \omega} 2^{-n} d(f_n(x), f_n(y))$
.
By the Banach-Alaoglu theorem, a closed ball of finite radius B is weak-* compact. The countable set
![]() ${{\{{\pi_i} \mid{i \in \omega}\}}}$
of retractions from (6) is separating on B, in the sense that:
${{\{{\pi_i} \mid{i \in \omega}\}}}$
of retractions from (6) is separating on B, in the sense that:
Furthermore, each
![]() $\pi_i$
is weak-* continuous. Thus, it suffices to take
$\pi_i$
is weak-* continuous. Thus, it suffices to take
![]() $f_n = \pi_n/2$
, and the claim follows from Rudin (Reference Rudin1991, Section 3.8(c), page 63) and Theorem 5.12.
$f_n = \pi_n/2$
, and the claim follows from Rudin (Reference Rudin1991, Section 3.8(c), page 63) and Theorem 5.12.
The metric
![]() $d_*$
on the carrier of
$d_*$
on the carrier of
![]() $\ell_{\infty}$
satisfies the following property
$\ell_{\infty}$
satisfies the following property
.
Corollary 5.18.
For each
![]() $p \in [1,\infty]$
, the metric
$p \in [1,\infty]$
, the metric
![]() $d_*$
induces the
$d_*$
induces the
![]() ${\overline{\tau}}_p$
-topology on closed balls of finite radius in
${\overline{\tau}}_p$
-topology on closed balls of finite radius in
![]() $\ell_{p}$
.
$\ell_{p}$
.
Proof. Let B be the closed ball in
![]() $\ell_{p}$
centered at
$\ell_{p}$
centered at
![]() $x_0$
with radius
$x_0$
with radius
![]() $r>0$
. Let B’ denote the closed ball in
$r>0$
. Let B’ denote the closed ball in
![]() $\ell_{\infty}$
centered at
$\ell_{\infty}$
centered at
![]() $x_0$
with radius r. The
$x_0$
with radius r. The
![]() ${\overline{\tau}}_p$
-topology on B is the restriction of the
${\overline{\tau}}_p$
-topology on B is the restriction of the
![]() ${\overline{\tau}}_\infty$
-topology on B’. The claim now follows from Proposition 5.17.
${\overline{\tau}}_\infty$
-topology on B’. The claim now follows from Proposition 5.17.
By going from
![]() $B_{p}$
to
$B_{p}$
to
![]() $\overline{B}_{p}$
, robustness with respect to the metric
$\overline{B}_{p}$
, robustness with respect to the metric
![]() $d_p$
is replaced by robustness with respect to the metric
$d_p$
is replaced by robustness with respect to the metric
![]() $d_*$
. Indeed, inequality (9) shows that for any subset S of
$d_*$
. Indeed, inequality (9) shows that for any subset S of
![]() $\lvert\thinspace {B_{p}} \thinspace\rvert$
its
$\lvert\thinspace {B_{p}} \thinspace\rvert$
its
![]() $\delta$
-neighborhood
$\delta$
-neighborhood
![]() $B(S,\delta)$
under
$B(S,\delta)$
under
![]() $d_p$
is included its
$d_p$
is included its
![]() $\delta$
-neighborhood under
$\delta$
-neighborhood under
![]() $d_*$
.
$d_*$
.
Proposition 5.19.
For every
![]() $C \in \mathbb{C}(B_{p})$
:
$C \in \mathbb{C}(B_{p})$
:
-
(1) The set
 $\iota_*(C)$
is the closure of C under the
$\iota_*(C)$
is the closure of C under the
 $d_*$
metric.
$d_*$
metric. -
(2) For every
 $x \in B_{p}$
,
$x \in B_{p}$
,
 $x\in \iota_*(C)$
if and only if: (10)
$x\in \iota_*(C)$
if and only if: (10) \begin{equation} \forall n \in \omega.\forall \delta>0. \exists y \in C.\forall i \in n. \quad d(x_i,y_i)<\delta .\end{equation}
\begin{equation} \forall n \in \omega.\forall \delta>0. \exists y \in C.\forall i \in n. \quad d(x_i,y_i)<\delta .\end{equation}
Proof. Claim (1) follows from Corollary 5.18. From it, we deduce that
![]() $x\in \iota_*(C)$
if and only if:
$x\in \iota_*(C)$
if and only if:
Thus, for the second claim, it suffices to prove that (10) and (11) are equivalent.
(10)⇒(11): For any given
![]() $\varepsilon > 0$
, choose n large enough such that
$\varepsilon > 0$
, choose n large enough such that
![]() $\varepsilon 2^{n-2} > 1$
and
$\varepsilon 2^{n-2} > 1$
and
![]() $\delta = \varepsilon / 2$
. By (10), there exists a
$\delta = \varepsilon / 2$
. By (10), there exists a
![]() $y \in C$
such that
$y \in C$
such that
![]() $\forall i \in n. \ d(x_i,y_i)<\delta$
. For this y we have:
$\forall i \in n. \ d(x_i,y_i)<\delta$
. For this y we have:
 \begin{align*} d_*(x,y) &= \sum_{i \in n} \frac{d(x_i, y_i)}{2^{i+1}} + \sum_{i \geq n} \frac{d(x_i, y_i)}{2^{i+1}} \\ &\leq \sum_{i \in n} \frac{\delta}{2^{i+1}} + \sum_{i \geq n} \frac{2}{2^{i+1}} \\ &\leq \delta + \frac{2}{2^n} \leq \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon.\end{align*}
\begin{align*} d_*(x,y) &= \sum_{i \in n} \frac{d(x_i, y_i)}{2^{i+1}} + \sum_{i \geq n} \frac{d(x_i, y_i)}{2^{i+1}} \\ &\leq \sum_{i \in n} \frac{\delta}{2^{i+1}} + \sum_{i \geq n} \frac{2}{2^{i+1}} \\ &\leq \delta + \frac{2}{2^n} \leq \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon.\end{align*}
(11)⇒(10): For any given
![]() $n \in \omega$
and
$n \in \omega$
and
![]() $\delta > 0$
, choose
$\delta > 0$
, choose
![]() $\varepsilon = \delta / 2^{n+1}$
. By (11), there exists a
$\varepsilon = \delta / 2^{n+1}$
. By (11), there exists a
![]() $y \in C$
such that
$y \in C$
such that
![]() $d_*(x,y) < \varepsilon$
, which implies that:
$d_*(x,y) < \varepsilon$
, which implies that:
From (12), we obtain
![]() $\forall i \in \omega. d(x_i, y_i) < \delta*2^{i-n}$
. In particular, for every
$\forall i \in \omega. d(x_i, y_i) < \delta*2^{i-n}$
. In particular, for every
![]() $i \in n$
, we have
$i \in n$
, we have
![]() $d(x_i, y_i) < \delta$
. This completes the proof of the second claim.
$d(x_i, y_i) < \delta$
. This completes the proof of the second claim.
5.2 Loss of precision
In this subsection, we discuss loss of precision through a few examples.
Example 5.20
(bounded, closed, non-convex, discrete). Take the sequences
![]() $(e_i \mid i \in \omega)$
as defined in (7), that is:
$(e_i \mid i \in \omega)$
as defined in (7), that is:
 \begin{align*} \forall n \in \omega. \quad e_i(n) \stackrel{\triangle}{=} \left\{ \begin{array}{ll} 0,& \text{ if } i \neq n,\\ 1, & \text{ if } i = n,\\ \end{array} \right.\end{align*}
\begin{align*} \forall n \in \omega. \quad e_i(n) \stackrel{\triangle}{=} \left\{ \begin{array}{ll} 0,& \text{ if } i \neq n,\\ 1, & \text{ if } i = n,\\ \end{array} \right.\end{align*}
and consider the set
![]() $C \stackrel{\triangle}{=} {{\{{e_i} \mid{i \in \omega}\}}}$
, which is a discrete, bounded, and closed subset of
$C \stackrel{\triangle}{=} {{\{{e_i} \mid{i \in \omega}\}}}$
, which is a discrete, bounded, and closed subset of
![]() $B_{p}$
for
$B_{p}$
for
![]() $p \in [1,\infty]$
. Using the metric
$p \in [1,\infty]$
. Using the metric
![]() $d_*$
of (8), we show that
$d_*$
of (8), we show that
![]() $\iota_*(C) = C \bigcup {{\left\{{0}\right\}}}$
.
$\iota_*(C) = C \bigcup {{\left\{{0}\right\}}}$
.
It is indeed clear that 0 is in the weak-* closure of C as:
Furthermore,
![]() $\forall i,j \in \omega. \ d_*(e_i,e_j) \leq 2^{-(i+2)} + 2^{-(j+2)}$
. This entails that
$\forall i,j \in \omega. \ d_*(e_i,e_j) \leq 2^{-(i+2)} + 2^{-(j+2)}$
. This entails that
![]() $\lim_{i,j \to \infty} d_*(e_i, e_j) = 0$
. Hence, the sequence
$\lim_{i,j \to \infty} d_*(e_i, e_j) = 0$
. Hence, the sequence
![]() $(e_i \mid {i \in \omega})$
is a Cauchy sequence under
$(e_i \mid {i \in \omega})$
is a Cauchy sequence under
![]() $d_*,$
and it can have only one limit point, i.e., zero.
$d_*,$
and it can have only one limit point, i.e., zero.
Example 5.21 (bounded, closed, non-convex, connected). Consider the unit sphere
![]() $S_p \stackrel{\triangle}{=} {{\{{s \in B_{p}} \mid{ {{{\lVert\thinspace {s}\thinspace\rVert}}}_p = 1}\}}}$
, which is norm-closed and non-convex. The weak-* closure of the unit sphere in
$S_p \stackrel{\triangle}{=} {{\{{s \in B_{p}} \mid{ {{{\lVert\thinspace {s}\thinspace\rVert}}}_p = 1}\}}}$
, which is norm-closed and non-convex. The weak-* closure of the unit sphere in
![]() $\lvert\thinspace {B_{p}} \thinspace\rvert$
is the entire unit ball
$\lvert\thinspace {B_{p}} \thinspace\rvert$
is the entire unit ball
![]() $\lvert\thinspace {B_{p}} \thinspace\rvert$
. In this case, the loss of precision is quite noticeable.
$\lvert\thinspace {B_{p}} \thinspace\rvert$
. In this case, the loss of precision is quite noticeable.
In Theorem 5.4, the assumption
![]() $p \not \in {{\left\{{ 1 , \infty}\right\}}}$
is crucial, as demonstrated in Example 5.22 and Proposition 5.25.
$p \not \in {{\left\{{ 1 , \infty}\right\}}}$
is crucial, as demonstrated in Example 5.22 and Proposition 5.25.
Example 5.22. (bounded, closed, convex,
![]() $p=\infty$
). Consider the set
$p=\infty$
). Consider the set
![]() $C \stackrel{\triangle}{=} c_0 \bigcap B_{\infty}$
, which is a bounded, closed, and convex subset of
$C \stackrel{\triangle}{=} c_0 \bigcap B_{\infty}$
, which is a bounded, closed, and convex subset of
![]() $B_{\infty}$
. In Section 4.6, we proved that
$B_{\infty}$
. In Section 4.6, we proved that
![]() $\iota_*(C) = B_{\infty}$
.
$\iota_*(C) = B_{\infty}$
.
Theorem 5.4 relies on the fact that norm-closed and convex subsets of reflexive Banach spaces are weakly closed. On the other hand, norm-closed and convex subsets of non-reflexive Banach spaces are not, in general, weak-* closed. Recall that the map
![]() $\eta_X$
in Definition 5.7 is a linear isometry which embeds X into X”. When X is not reflexive, we have
$\eta_X$
in Definition 5.7 is a linear isometry which embeds X into X”. When X is not reflexive, we have
![]() $X'' \setminus X \neq \emptyset$
.
$X'' \setminus X \neq \emptyset$
.
Proposition 5.23.
If X is a non-reflexive Banach space and
![]() $\theta \in X'' \setminus X$
, then the kernel
$\theta \in X'' \setminus X$
, then the kernel
![]() $\theta^{-1}(0)$
of
$\theta^{-1}(0)$
of
![]() $\theta$
is a closed linear sub-space of X’ which is not weak-* closed.
$\theta$
is a closed linear sub-space of X’ which is not weak-* closed.
Proof. This is a consequence of Conway (Reference Conway1990, Theorem 3.1, page 108) and Rudin (Reference Rudin1991, Theorem 3.10, page 64).
Using the following result, for any given non-reflexive Banach space, one may construct many examples of sets for which there is a loss of precision, provided the space is the dual of another Banach space, i.e., has a pre-dual. This rules out spaces such as
![]() $c_0$
which have no pre-duals (Albiac and Kalton, Reference Albiac and Kalton2006, Theorem 6.3.7).
$c_0$
which have no pre-duals (Albiac and Kalton, Reference Albiac and Kalton2006, Theorem 6.3.7).
Corollary 5.24. (bounded, closed, convex, non-reflexive with pre-dual). If X is a non-reflexive Banach space, B is the closed unit ball in X’ and
![]() $\theta \in X'' \setminus X$
, then
$\theta \in X'' \setminus X$
, then
![]() $C \stackrel{\triangle}{=} B \bigcap \theta^{-1}(0)$
is closed and convex in X’—hence, weakly closed—but not weak-* closed.
$C \stackrel{\triangle}{=} B \bigcap \theta^{-1}(0)$
is closed and convex in X’—hence, weakly closed—but not weak-* closed.
Proof. As a consequence of Proposition 5.23, the set C is closed and convex, hence, weakly closed. By Conway (Reference Conway1990, Corollary 12.6, page 160), however, C cannot be weak-* closed.
In general, an exact description of the weak-* closures of sets C in Corollary 5.24 is not known. There are, however, inner and outer approximations available in the literature. For instance, according to Jameson (Reference Jameson1982, Proposition 2), the weak-* closure of C must contain a closed ball centered at the origin. Proposition 5.25 gives an instance of this result, which we prove directly.
Proposition 5.25. (bounded, closed, convex,
![]() $p=1$
). If
$p=1$
). If
![]() $C \stackrel{\triangle}{=} {{\{{x \in B_{1}} \mid{\sum_{n \in \omega} x_n = 0}\}}}$
, D is the closed ball in
$C \stackrel{\triangle}{=} {{\{{x \in B_{1}} \mid{\sum_{n \in \omega} x_n = 0}\}}}$
, D is the closed ball in
![]() $\ell_1$
centered at 0 with radius
$\ell_1$
centered at 0 with radius
![]() $1/2$
, and
$1/2$
, and
![]() $\overline{C}$
is the
$\overline{C}$
is the
![]() $\tau_1^*$
-closure of C in
$\tau_1^*$
-closure of C in
![]() $B_{1}$
, then:
$B_{1}$
, then:
-
(1) C is closed and convex—hence, also weakly closed—in
 $B_{1}$
. But, C is not weak-* closed.
$B_{1}$
. But, C is not weak-* closed. -
(2)
 $D \setminus C \neq \emptyset$
.
$D \setminus C \neq \emptyset$
. -
(3)
 $D \subset \overline{C} \subset B_{1}$
, where both inclusions are strict.
$D \subset \overline{C} \subset B_{1}$
, where both inclusions are strict.
Proof. Take
![]() $X = c_0$
(which implies that
$X = c_0$
(which implies that
![]() $X' = \ell_{1}$
and
$X' = \ell_{1}$
and
![]() $X'' = \ell_{\infty}$
) and let
$X'' = \ell_{\infty}$
) and let
![]() $\theta = 1^\omega \in \ell_{\infty} \setminus c_o$
, i.e., the constant sequence of ones. We have
$\theta = 1^\omega \in \ell_{\infty} \setminus c_o$
, i.e., the constant sequence of ones. We have
![]() $C = B_{1} \bigcap \theta^{-1}(0)$
.
$C = B_{1} \bigcap \theta^{-1}(0)$
.
-
(1) Follows from Corollary 5.24.
-
(2)
 $\left(\frac{1}{2^{n+2}}\mid {n \in \omega} \right) \in D \setminus C$
.
$\left(\frac{1}{2^{n+2}}\mid {n \in \omega} \right) \in D \setminus C$
. -
(3) Assume that
 $x = (x_n \mid {n \in \omega}) \in D$
. For any
$x = (x_n \mid {n \in \omega}) \in D$
. For any
 $n \in \omega$
and
$n \in \omega$
and
 $\delta > 0$
, consider
$\delta > 0$
, consider
 $\hat{x} = (\hat{x}_i \mid {i \in \omega})$
defined as follows:
$\hat{x} = (\hat{x}_i \mid {i \in \omega})$
defined as follows:
We have
![]() $\theta(\hat{x}) = \sum_{i \in \omega} \hat{x}_i = 0$
. Furthermore,
$\theta(\hat{x}) = \sum_{i \in \omega} \hat{x}_i = 0$
. Furthermore,
![]() ${{{\lVert\thinspace {\hat{x}}\thinspace\rVert}}}_1 \leq 2 {{{\lVert\thinspace {x}\thinspace\rVert}}}_1 \leq 1$
. Hence,
${{{\lVert\thinspace {\hat{x}}\thinspace\rVert}}}_1 \leq 2 {{{\lVert\thinspace {x}\thinspace\rVert}}}_1 \leq 1$
. Hence,
![]() $\hat{x} \in \theta^{-1}(0) \bigcap$
$\hat{x} \in \theta^{-1}(0) \bigcap$
![]() $B_{1} = C$
. Clearly, for all
$B_{1} = C$
. Clearly, for all
![]() $i \in n$
, we have
$i \in n$
, we have
![]() $d(x_i, \hat{x}_i) = 0 \leq \delta$
. Therefore, equation (10) of Proposition 5.19 holds, and we have
$d(x_i, \hat{x}_i) = 0 \leq \delta$
. Therefore, equation (10) of Proposition 5.19 holds, and we have
![]() $D \subseteq \overline{C}$
.
$D \subseteq \overline{C}$
.
Take the sequence
![]() $y = (y_n \mid {n \in \omega})$
defined as follows:
$y = (y_n \mid {n \in \omega})$
defined as follows:

Then,
![]() $y \in C \setminus D \subseteq \overline{C} \setminus D$
. Thus, we have proved that
$y \in C \setminus D \subseteq \overline{C} \setminus D$
. Thus, we have proved that
![]() $D \subset \overline{C}$
.
$D \subset \overline{C}$
.
It remains to prove that
![]() $B_{1} \setminus \overline{C} \neq \emptyset$
. Take the sequence
$B_{1} \setminus \overline{C} \neq \emptyset$
. Take the sequence
![]() $z = (z_n \mid {n \in \omega})$
defined as follows:
$z = (z_n \mid {n \in \omega})$
defined as follows:

Clearly,
![]() $z \in B_{1}$
. We use Proposition 5.19 to prove that
$z \in B_{1}$
. We use Proposition 5.19 to prove that
![]() $z \not \in \overline{C}$
. In (10), choose
$z \not \in \overline{C}$
. In (10), choose
![]() $n=1$
and
$n=1$
and
![]() $\delta = 1/2$
. For any given
$\delta = 1/2$
. For any given
![]() $\hat{z} \in C$
, we have
$\hat{z} \in C$
, we have
![]() $\sum_{n \in \omega} \hat{z}_n = 0$
. Thus,
$\sum_{n \in \omega} \hat{z}_n = 0$
. Thus,
![]() $\sum_{n=1}^\infty \hat{z}_n = -\hat{z}_0$
, which implies that:
$\sum_{n=1}^\infty \hat{z}_n = -\hat{z}_0$
, which implies that:
On the other hand, as
![]() $\hat{z} \in C$
, we must have
$\hat{z} \in C$
, we must have
![]() ${{{\lVert\thinspace {\hat{z}}\thinspace\rVert}}}_1 \leq 1$
. As a result:
${{{\lVert\thinspace {\hat{z}}\thinspace\rVert}}}_1 \leq 1$
. As a result:
By combining (13) and (14), we obtain
![]() $\lvert\thinspace {\hat{z}_0} \thinspace\rvert \leq 1/2$
, which implies
$\lvert\thinspace {\hat{z}_0} \thinspace\rvert \leq 1/2$
, which implies
![]() $1 - \hat{z}_0 \geq 1/2$
, equivalently
$1 - \hat{z}_0 \geq 1/2$
, equivalently
![]() $d(z_0, \hat{z}_0) \geq 1/2 = \delta$
.
$d(z_0, \hat{z}_0) \geq 1/2 = \delta$
.
6. Concluding Remarks
The results in this paper are part of an overall study of robust maps. We have chosen the theory of
![]() $\omega$
-continuous lattices, within which computability can be studied using the framework of effectively given domains (Smyth, Reference Smyth1977), and robustness can be analyzed using the Robust topology (Definition 2.25) over the lattice of closed subsets of the state space.
$\omega$
-continuous lattices, within which computability can be studied using the framework of effectively given domains (Smyth, Reference Smyth1977), and robustness can be analyzed using the Robust topology (Definition 2.25) over the lattice of closed subsets of the state space.
In a related work, Edalat (Reference Edalat1995) has considered locally compact Hausdorff spaces instead of metric spaces and has worked with the domain of compact subsets (ordered by reverse inclusion) instead of the complete lattice of closed subsets. Furthermore, he has investigated the relationship between the Scott topology and the upper Vietoris topology, but has not studied robustness. The Robust topology lies in between the Scott and the upper Vietoris topologies (Theorem 2.27).
The case of compact metric spaces has been studied in Moggi et al. (Reference Moggi, Farjudian, Duracz and Taha2018). This suffices to deal with the input space of typical machine learning systems and the state space of common hybrid systems. In this paper, the focus has been non-compact metric spaces, for which, a novel approach has been presented based on approximation of the space via a (growing) sequence of compact metric sub-spaces. Non-compact spaces are relevant when dealing with perturbations of the model parameters of a system, e.g., perturbations of the activation function(s) of a neural network, or the flow F and jump G relations of a hybrid system
![]() $(\mathbb{S},F,G)$
.
$(\mathbb{S},F,G)$
.
We presented a detailed account of some examples, including (closed bounded subsets of) infinite-dimensional Banach spaces, and analyzed the important issue of precision, when it is retained, and when precision is lost. In particular, we have obtained a complete characterization of the closed subsets of reflexive spaces
![]() $\ell_{p}$
(i.e., those with
$\ell_{p}$
(i.e., those with
![]() $1 < p < \infty$
), for which there is no loss of precision (Theorem 5.4).
$1 < p < \infty$
), for which there is no loss of precision (Theorem 5.4).
All examples studied in this paper are sequence spaces. As such, studying other relevant spaces provides an immediate direction for future work. For instance, let
![]() $\Omega \subseteq \mathbb{R}^n$
be an open set. Lebesgue spaces
$\Omega \subseteq \mathbb{R}^n$
be an open set. Lebesgue spaces
![]() $L^p(\Omega)$
are examples for future work, which are relevant in the study of partial differential equations (Brezis, Reference Brezis2011).
$L^p(\Omega)$
are examples for future work, which are relevant in the study of partial differential equations (Brezis, Reference Brezis2011).
Other cases for future study include infinite-dimensional feature spaces arising in machine learning and spaces of bounded measures. In particular, by applying our results to (closed subsets of) probability measures, we obtain a framework for computation of probability measures using finitary approximations. It will be interesting to compare the finitary approximations obtained in this way, with those obtained by Edalat (Reference Edalat1997) for computation of probability measures over separable metric spaces.
Competing interests
The authors declare none.